考察cpp的静态绑定
|
会打印什么?
答案以及分析
答案: 打印1之后崩溃
真正的原因是:
因为对于非虚成员函数,C++这门语言是静态绑定的。这也是C++语言和其它语言Java, Python的一个显著区别。以此下面的语句为例:somenull->foo();这语句的意图是:调用对象somenull的foo成员函数。如果这句话在Java或Python等动态绑定的语言之中,编译器生成的代码大概是:找到somenull的foo成员函数,调用它。
(注意,这里的找到是程序运行的时候才找的,这也是所谓动态绑定的含义:运行时才绑定这个函数名与其对应的实际代码。有些地方也称这种机制为迟绑定,晚绑定。)但是对于C++。为了保证程序的运行时效率,C++的设计者认为凡是编译时能确定的事情,就不要拖到运行时再查找了。
所以C++的编译器看到这句话会这么干:
- 查找somenull的类型,发现它有一个非虚的成员函数叫foo。(编译器干的)
- 找到了,在这里生成一个函数调用,直接调B::foo(somenull)。
所以到了运行时,由于foo()函数里面并没有任何需要解引用somenull指针的代码,所以真实情况下也不会引发segment fault。这里对成员函数的解析,和查找其对应的代码的工作都是在编译阶段完成而非运行时完成的,这就是所谓的静态绑定,也叫早绑定。正确理解C++的静态绑定可以理解一些特殊情况下C++的行为。
求最大公约数
求 a 和 b 的最大公约数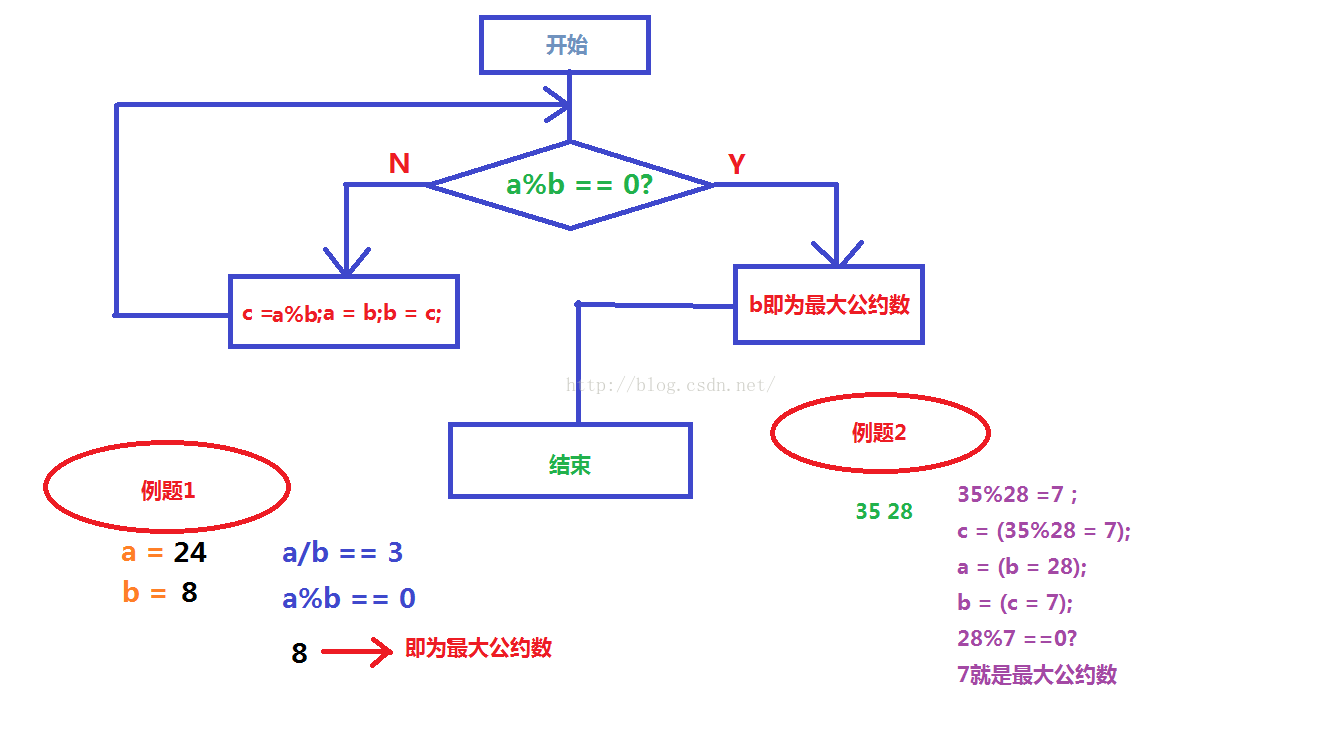
int measure(int a, int b) |
棋盘/格子问题
在如下7*5的棋盘中,请计算从A移动到B一共有多少走法?要求每次只能向上或向右移动一格,并且不能经过P。(答案为492)
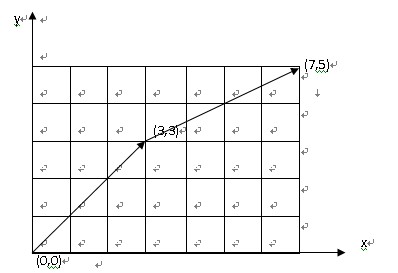
给定一个M*N的格子或棋盘,从左下角走到右上角的走法总数(每次只能向右或向上移动一个方格边长的距离)
运用动态规划来解答 :
我们可以把棋盘的左下角看做二维坐标的原点(0,0),把棋盘的右上角看做二维坐标(M,N)(坐标系的单位长度为小方格的变长)
用f(i,j)表示移动到坐标f(i,j)的走法总数,其中0=<i,j<=n,设f(m,n)代表从坐标(0,0)到坐标(m,n)的移动方法,则
f(m,n)=f(m-1,n)+f(m,n-1).
于是状态f(i,j)的状态转移方程为:
f(i,j)=f(i-1,j)+f(i,j-1) if i,j>0
f(i,j)=f(i,j-1) if i=0
f(i,j)=f(i-1,j) if j=0
初始情况就为:f(0,0)=0, f(0,1)=1, f(1,0)=1,这个问题可以在时间O(n^2),空间O(n^2)内求解,非递归解.
所以答案为 492 =
SumWaysOfMoveOnChessBoard(7, 5) - SumWaysOfMoveOnChessBoard(3, 3) * SumWaysOfMoveOnChessBoard(7 - 3, 5 - 3) |
递归解
int SumWaysOfMoveOnChessBoard_Recursion(int m, int n) |
非递归解
int SumWaysOfMoveOnChessBoard_NonRecursion_RawArray(int m, int n) |
大数加法/乘法
大数加法思路 :
模拟小学列竖式
9 8
+ 2 1
-------------
(1)(1)(9)
大数乘法思路 :
模拟乘法累加 - 改进
简单来说,方法二就是先不算任何的进位,也就是说,将每一位相乘,相加的结果保存到同一个位置,到最后才计算进位。
例如:计算98×21,步骤如下
9 8
× 2 1
-------------
(9)(8) <---- 第1趟: 98×1的每一位结果
(18)(16) <---- 第2趟: 98×2的每一位结果
-------------
(18)(25)(8) <---- 这里就是相对位的和,还没有累加进位
这里唯一要注意的便是进位问题,我们可以先不考虑进位,当所有位对应相加,产生结果之后,再考虑。
从右向左依次累加,如果该位的数字大于10,那么我们用取余运算,在该位上只保留取余后的个位数,而将十位数进位(通过模运算得到)累加到高位便可,循环直到累加完毕。
void BigIntAddition(char* bigIntA, char* bigIntB) |
最长公共子串
问题:有两个字符串str和str2,求出两个字符串中最长公共子串长度。
比如:str=acbcbcef,str2=abcbced,则str和str2的最长公共子串为bcbce,最长公共子串长度为5。
算法思路:
1、把两个字符串分别以行和列组成一个二维矩阵。
2、比较二维矩阵中每个点对应行列字符中否相等,相等的话值设置为1,否则设置为0。
3、通过查找出值为1的最长对角线就能找到最长公共子串。
针对于上面的两个字符串我们可以得到的二维矩阵如下: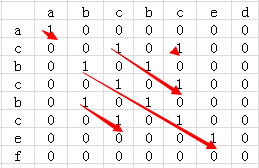
从上图可以看到,str和str2共有5个公共子串,但最长的公共子串长度为5。
为了进一步优化算法的效率,我们可以再计算某个二维矩阵的值的时候顺便计算出来当前最长的公共子串的长度,
即某个二维矩阵元素的值由 item[i][j]=1 演变为 item[i][j]=1 +item[i-1][j-1] ,这样就避免了后续查找对角线长度的操作了。修改后的二维矩阵如下: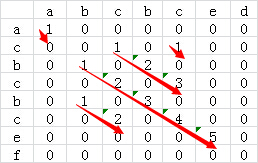
故状态转移方程
X[i] == Y[j],dp[i][j] = dp[i-1][j-1] + 1
X[i] != Y[j],dp[i][j] = 0
int LongestCommonSubstring(char* strA, char* strB) |