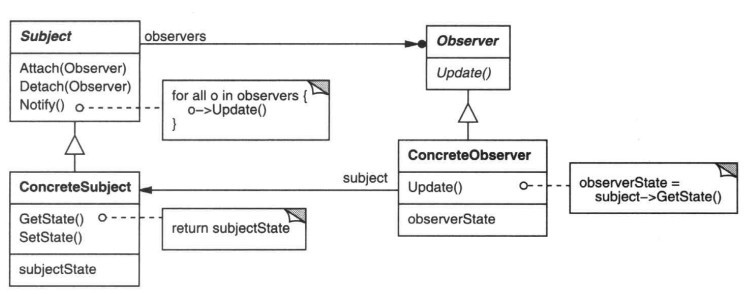
c++中对new申请的内存的释放方式有delete和delete[]两种方式,到底这两者有什么区别呢?
疑问
我们通常从教科书上看到这样的说明:
delete 释放new分配的单个对象指针指向的内存
delete[] 释放new分配的对象数组指针指向的内存
那么,按照教科书的理解,我们看下下面的代码:
int *a = new int[10]; |
肯定会有很多人说方式1肯定存在内存泄漏,是这样吗?
针对基本数据类型
针对简单类型 使用new分配后的不管是数组还是非数组形式内存空间用两种方式均可 如:int *a = new int[10];
delete a;
delete [] a;
此种情况中的释放效果相同,原因在于:分配简单类型内存时,内存大小已经确定,系统可以记忆并且进行管理,在析构时,系统并不会调用析构函数,
它直接通过指针可以获取实际分配的内存空间,哪怕是一个数组内存空间(在分配过程中 系统会记录分配内存的大小等信息,此信息保存在结构体_CrtMemBlockHeader中,
具体情况可参看VC安装目录下CRT\SRC\DBGDEL.cpp)
针对复杂数据类型
针对类Class,两种方式体现出具体差异
当你通过下列方式分配一个类对象数组:
class A |
再看下面代码:
class A{ |
- delete []pas; //详细流程
答案见下文总结 - delete []pa; //会发生什么
答案是调用未知次数的A的析构函数. 因为delete[]会去通过pa+offset找一个基于pa的偏移量找一个内存里的数据, 他假定这个内存里放了要调用析构的次数n这个数据, 而这个内存里到底是多少是未知的. - delete pas; //哪些指针会变成野指针
答案是pas和A[0]中的指针会变成野指针. 因为只有这两个指针指向的内存被释放了, 也就是说, 仅释放了pas指针指向的这个数组的全部内存空间, 以及只调用了a[0]对象的析构函数
总结
所以总结下就是,关于 new[] 和 delete[],其中又分为两种情况:
- 基本数据类型
对于像int/char/long/int*/struct等等简单数据类型,由于对象没有destructor,所以用delete 和delete [] 是一样的! - 复杂数据类型类型
- delete ptr 代表用来释放内存,且只用来释放ptr指向的内存。
- delete[] rg 用来释放rg指向的内存!!还逐一调用数组中每个对象的destructor!!