数据结构三之二叉搜索树的增删查

数据结构二之二叉树的遍历和交换左右孩子

STL之队列和双端队列和栈的比较

有了二叉树的基础, 我们继续学习二叉搜索树.

二叉搜索树的定义

二叉查找树(Binary Search Tree, 简称”BST”), 又名”二叉搜索树”或”二叉排序树”:
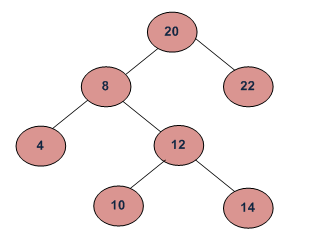
它或者是一棵空树，或者是具有下列性质的二叉树： 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

. . .

注 :
我们本文中二叉树的二叉链式存储方案的代码表示为

typedef struct BinaryTreeNode
{
	void *data;
	BinaryTreeNode *LeftNode;
	BinaryTreeNode *RightNode;
}BTN, *BTNP;

二叉搜索树的查询

BTNP SearchBST(BTNP btnp, char key_data)
{
	while (btnp)
	{
		if ( key_data < (*(char *)(btnp->data)) )
		{
			btnp = btnp->LeftNode;
		}
		else if ( key_data >(*(char *)(btnp->data)) )
		{
			btnp = btnp->RightNode;
		}
		else
		{
			cout << "found" << endl;
			return btnp;
		}
	}
	cout << "not found" << endl;
	return nullptr;
}

二叉搜索树的插入

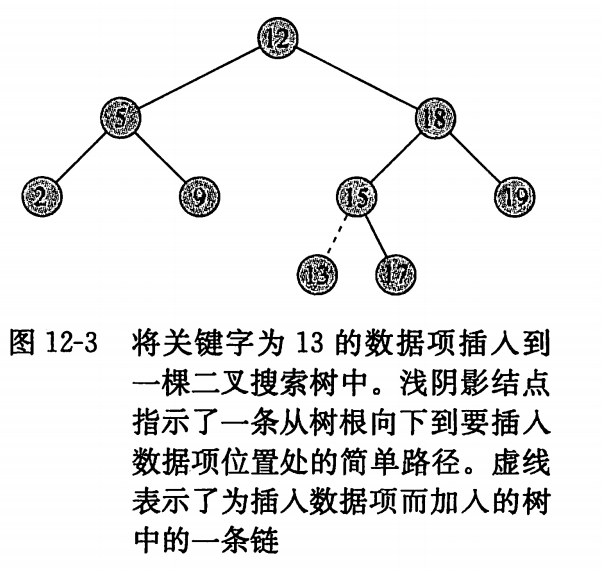
void InsertBST(BTNP &btnp, char key_data)
{

	char * temp_key_data = new char;
	*temp_key_data = key_data;

	BTNP new_btnp = new BTN;
	new_btnp->data = temp_key_data;
	new_btnp->LeftNode = nullptr;
	new_btnp->RightNode = nullptr;

	if (!btnp)
	{
		btnp = new_btnp;
		return;
	}

	BTNP temp_btnp = btnp;
	BTNP parent_btnp = nullptr;
	bool is_left = true;
	while (temp_btnp)
	{
		parent_btnp = temp_btnp;
		if (key_data < (*(char *)(temp_btnp->data)))
		{
			temp_btnp = temp_btnp->LeftNode;
			is_left = true;
		}
		else if (key_data > (*(char *)(temp_btnp->data)))
		{
			temp_btnp = temp_btnp->RightNode;
			is_left = false;
		}
		else
		{
			cout << "already has a same key_data" << endl;
			return;
		}
	}

	if (is_left == true)
	{
		parent_btnp->LeftNode = new_btnp;
	}
	else
	{
		parent_btnp->RightNode = new_btnp;
	}
}

二叉搜索树之删除某个结点

void DeleteBinaraySearchTree(BTNP &btnp, char key)
{
	// 第一步 : 查找是否有这个key
	BTNP parentBTNP = NULL;
	bool isLeft = true;

	BTNP tempBNTP = btnp;

	while (tempBNTP)
	{
		if (*(char*)tempBNTP->data > key)
		{
			parentBTNP = tempBNTP;
			tempBNTP = tempBNTP->LeftNode;
			isLeft = true;
		}
		else if (*(char*)tempBNTP->data < key)
		{
			parentBTNP = tempBNTP;
			tempBNTP = tempBNTP->RightNode;
			isLeft = false;
		}
		else
		{
			break;
		}
	}

	if (!tempBNTP)
	{
		cout << "not found this key!!" << endl;
		return;
	}

	cout << "found this key!!" << endl;

	// 第二步 : 我们得处里key结点没有父结点的情况
	if (!parentBTNP)
	{
		delete (char *)btnp->data;
		btnp->data = NULL;

		delete btnp;
		btnp = NULL;

		cout << "test" << endl;

		return;
	}
	else
	{
		// 第三步 : 我们得处里key结点有父结点的4种情况

		// 情况1
		if (tempBNTP->LeftNode == NULL && tempBNTP->RightNode == NULL)
		{
			if (isLeft)
			{
				parentBTNP->LeftNode = NULL;
			}
			else
			{
				parentBTNP->RightNode = NULL;
			}
		}
		// 情况2
		else if (tempBNTP->LeftNode == NULL)
		{
			if (isLeft)
			{
				parentBTNP->LeftNode = tempBNTP->RightNode;
			}
			else
			{
				parentBTNP->RightNode = tempBNTP->RightNode;
			}
		}
		// 情况3
		else if (tempBNTP->RightNode == NULL)
		{
			if (isLeft)
			{
				parentBTNP->LeftNode = tempBNTP->LeftNode;
			}
			else
			{
				parentBTNP->RightNode = tempBNTP->LeftNode;
			}
		}
		// 情况4
		else if (tempBNTP->LeftNode != NULL && tempBNTP->RightNode != NULL)
		{
			// 情况4比较复杂, 我们得找到key结点的后继
			// (后继 : 一个结点x的后继是大于x.key的最小关键字的结点)
			// 因为情况4中的key结点左孩子和右孩子都不为空, 
			// 所以key结点的后继 successorBTNP 肯定位于key结点的右子树中,
			// 且 successorBTNP 没有左孩子( 不然 successorBTNP 的左孩子就是key结点的后继了嘛)
			BTNP tempTempBNTP = tempBNTP->RightNode;

			// key结点的后继
			BTNP successorBTNP = NULL;

			// key结点的后继的父结点
			BTNP successorParentBTNP = NULL;

			while (tempTempBNTP)
			{
				successorBTNP = tempTempBNTP;
				if (tempTempBNTP && tempTempBNTP->LeftNode && tempTempBNTP->LeftNode->LeftNode == NULL)
				{
					successorParentBTNP = tempTempBNTP;
				}
				tempTempBNTP = tempTempBNTP->LeftNode;
			}

			// 情况4又分两种情况, 如下 : 
			// 第一种情况 A 是 successorBTNP 是 key 的右孩子;
			// 第二种情况 B 是 successorBTNP 在 key 的右子树中, 但并不是 successorBTNP 本身并不是 key 的右孩子

			// 情况 A : 
			if (successorBTNP == tempBNTP->RightNode)
			{
				// 用 key 结点的后继 successorBTNP 来替代 key 结点
				if (isLeft)
				{
					parentBTNP->LeftNode = successorBTNP;
				}
				else
				{
					parentBTNP->RightNode = successorBTNP;
				}
			}
			// 情况 B :
			else
			{
				// 如果 successorBTNP 有右子树, 则用 successorBTNP 的右子树 代替 原来 successorBTNP 的位置.
				if (successorBTNP->RightNode)
				{
					successorParentBTNP->LeftNode = successorBTNP->RightNode;
				}

				// 用 key 结点的后继 successorBTNP 的data来替换 key 结点的data
				char * tempChar = new char;
				*tempChar = *(char *)successorBTNP->data;
				tempBNTP->data = tempChar;
				tempBNTP = successorBTNP;

				// 下面注释的这块代码可以用上面这两4行代替
				// if (isLeft)
				// {
				// 	parentBTNP->LeftNode = successorBTNP;
				// 	successorBTNP->RightNode = tempBNTP->RightNode;
				// 	successorBTNP->LeftNode = tempBNTP->LeftNode;
				// }
				// else
				// {
				// 	parentBTNP->RightNode = successorBTNP;
				// 	successorBTNP->RightNode = tempBNTP->RightNode;
				// 	successorBTNP->LeftNode = tempBNTP->LeftNode;
				// }
			}

		}

		// 记得释放 key 结点
		delete (char *)tempBNTP->data;
		tempBNTP->data = NULL;

		delete tempBNTP;
		tempBNTP = NULL;
	}
}

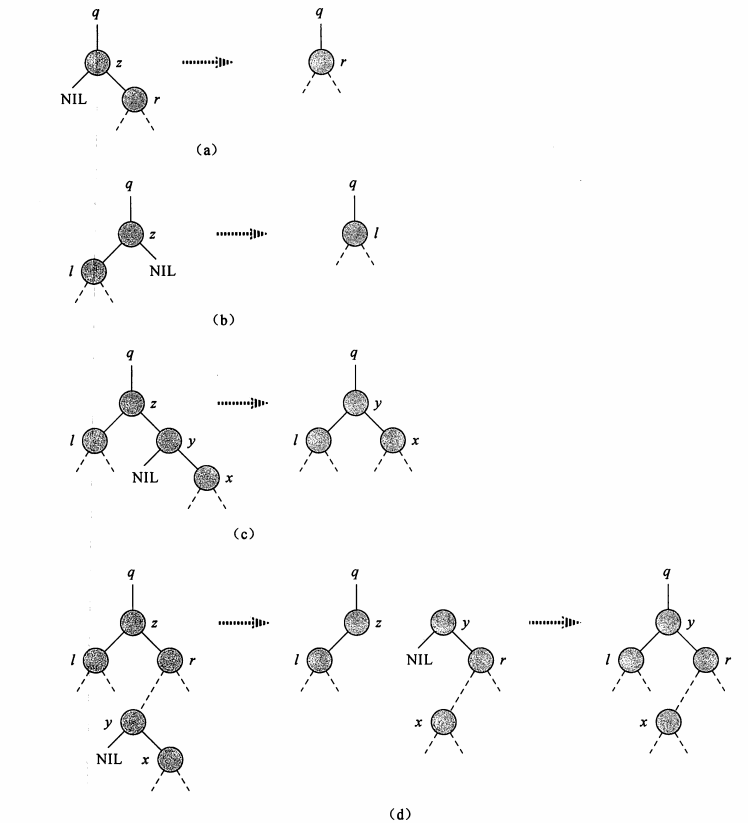
二叉搜索树之找最低公共祖先

给定二叉搜索树（BST）中两节点，找出他们的最低公共祖先(LeastCommonAncestors, 简称LCA)。

例如对于本文第一张图的LCA为 :

• LCA(4， 14)=8;
• LCA(8， 10)=8.

思路:

利用BST的性质, 假设n1,n2都在BST中，并且n1 < n2。则有 :

• 在遍历过程中，遇到的第一个值介于n1和n2之间的节点n，也即n1 =< n <= n2, 就是n1和n2的LCA。
• 在遍历过程中，如果节点的值比n1和n2都大，那么LCA在节点的左子树。
• 在遍历过程中，如果节点的值比n1和n2都小，那么LCA在节点的右子树。

void LeastCommonAncestorsBinaraySearchTree(BTNP btnp, char key1, char key2)
{
	if (!btnp)
	{
		cout << "the BST is null" << endl;
		return;
	}

	if (key1 == key2)
	{
		cout << "key1 == key2, so this is not a BST" << endl;
		return;
	}

	if (!SearchBinarySearchTree(btnp, key1))
	{
		cout << "key1 not found" << endl;
		return;
	}

	if (!SearchBinarySearchTree(btnp, key2))
	{
		cout << "key2 not found" << endl;
		return;
	}

	while (btnp)
	{
		char curChar = *(char *)(btnp->data);

		if (curChar < key1 && curChar < key2)
		{
			btnp = btnp->RightNode;
		}
		else if (curChar > key1 && curChar > key2)
		{
			btnp = btnp->LeftNode;
		}
		else 
		{
			cout << "LeastCommonAncestors is " << curChar << endl;
			return;
		}
	}
}

参考

<< 算法导论 >>

DataStructure Algo

数据结构二之二叉树的遍历和交换左右孩子

STL之队列和双端队列和栈的比较