只谈一下单链表, 链表实在是太重要, 是前面两篇说算法博客的基础, 了解了其应用和衍生, 再去了解其本身就有动力了
存储结构
typedef struct Node |
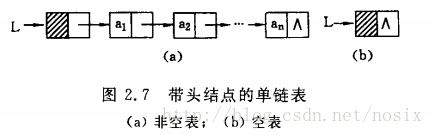
- 链表中第一个结点的存储位置叫做头指针
- 头指针和头结点不同,头结点即第一个结点,头指针是指向第一个结点的指针。链表中可以没有头结点,但不能没有头指针。
- 如果链表有头结点,那么头指针就是指向头结点数据域的指针。
- 单链表也可以没有头结点
头结点的优点:
- 头结点是为了操作的统一与方便而设立的,放在第一个元素结点之前,其数据域一般无意义(当然有些情况下也可存放链表的长度、用做监视哨等等)。
- 有了头结点后,对在第一个元素结点前插入结点和删除第一个结点,其操作与对其它结点的操作统一了。
有头结点和无头结点的建立链表方法头插法
include <stdio.h> |
运行结果:3 2 1
0 3 2 1
提示:没有 0 的为无头结点的头插法输出结果,有 0 的为有头结点的头插法的输出结果
在O(1)时间删除链表结点
给定单链表的头指针和一个结点指针, 定义一个函数在 O(1)时间删除该结点.
思路 :
如果要遍历找到该结点的前一个结点p, 来改变结点p的下一个结点指向的这种解法肯定是O(n)时间复杂度了.
那是不是一定需要得到被删除的结点的前一个结点呢?
答案是否定的。我们可以很方便地得到要删除的结点的下一个结点。如果我们把下一个结点的内容复制到需要删除的结点上覆盖原有的内容,再把下一个结点删除,那是不是就相当于把当前需要删除的结点删除了?
找一个单链表的中间结点
算法思想 :
(快慢指针的使用)设置两个指针,一个每次移动两个位置,一个每次移动一个位置,当第一个指针到达尾节点时,第二个指针就达到了中间节点的位置
判断链表中是否有环
算法思想 :
(快慢指针的使用)链表中有环,其实也就是自相交. 用两个指针pslow和pfast从头开始遍历链表,pslow每次前进一个节点,pfast每次前进两个结点,若存在环,则pslow和pfast肯定会在环中相遇,若不存在,则pslow和pfast能正常到达最后一个节点
判断两个链表是否相交, 假设两个链表均不带环
算法思想 :
如果两个链表相交于某一节点,那么在这个相交节点之后的所有节点都是两个链表所共有的。也就是说,如果两个链表相交,那么最后一个节点肯定是共有的。先遍历第一个链表,记住最后一个节点,然后遍历第二个链表,到最后一个节点时和第一个链表的最后一个节点做比较,如果相同,则相交,否则不相交。
从尾到头打印链表
有两种解法 :
- 反转链表解法 : 反转链表之后再从头到尾打印 (这样会改变原来的链表)
- 栈存储解法(比较简单, 本文不详讲了) : 用栈存储之后再逐个出栈一一打印 (这样不会改变原来的链表)
反转链表解法
比如一个链表:
头结点->A->B->C->D->E
反转成为:
头结点->E->D->C->B->A
算法思想 :
第一轮 : 头结点->A->B->C->D->E
第二轮 : 头结点->B->A->C->D->E
第三轮 : 头结点->C->B->A->D->E
第四轮 : 头结点->D->C->B->A->E
第五轮 : 头结点->E->D->C->B->A
算法cpp实现:
手写的代码, 已经跑过了,可直接用
下面代码中反转函数为 ReverseList , 且有详细注释以及总结
|
|
|