Only Prime - Algo Meta Top 100

Posted on | In

References

. . .

Meta面经1

补充内容 (2024-09-11 09:55 +08:00):
今天面完了5轮onsite，3 coding + bq+ sd，下面是面试前我自己整理的地理面经（3月到现在），onsite和电面的题目全在里面。如果时间不多，1～2个月内就面试，你看这一个帖子差不多就够了
面senior的别担心算法，出的题目都是看一眼就知道答案。几年前拿过meta offer，当时还被面了2轮hard，现在算法要求降低很多。

algo

算法题目，下面是leetcode题号:

  • 1 - 100: 7, 19, 21, 23, 26, 31, 34, 39, 43, 50, 56, 60, 62, 65, 71, 76, 79, 88
  • 101 - 200: 116, 121, 125, 127, 129, 133, 138, 140, 146, 162, 190, 199, 200
  • 201 - 400: 207, 210, 215, 219, 224, 227, 236, 249, 266, 283, 295, 301, 314, 317, 332, 339(不是给List，而是给字符串，可以用stack解题), 346, 347, 380
  • 401 - 1000: 408, 426, 435, 437, 438, 443, 447, 494, 499, 523, 528, 543, 560, 658, 680, 721, 739(单调栈的典型应用 www.geeksforgeeks.org), 791, 827, 934, 938, 973, 986, 987
  • Above 1000: 1004, 1047, 1060, 1091, 1123, 1161, 1209, 1216, 1249, 1382, 1539, 1570, 1644, 1650, 1762, 1778

sd

  1. Design a chess game, 要求可以撤回上一步
  2. 游戏leaderboard，需要有global&friends排名。这题准备过 但是面试官侧重点是怎么去sort我是没想到的
    1. 需要返回当前整个游戏的top N player、当前用户的前后N个player
    2. 返回当前用户朋友的top N player、当前用户朋友的前后N个player
  3. Hacker version Web crawler
  4. 有一些限定条件，比如说一万台机器，尽可能让每台机器的load evenly distributed。
  5. Design an Ads Aggregation System (广告点击)
  6. facebook 評論系統: user1 看到某個post1, user1 write comment, user2 看到post2, write comment, 同時要通知user1
  7. design zoom
  8. Design instagram
  9. Design ig auction: 设计一个auction system。 用户可以view current bid price 然就可以bid with higher price。 主要问了如果bid at same‍‍‌‍‍‍‍‌‌‌‍‌‍‌‍‍‍‌‍‌ price 怎么解决conflict。以及怎么scale一个很hot的auction。
  10. ig newsfeed, 怎么处理new post来通知用户的情况
  11. design dropbox. 全程drive对话，自己说哪里是bottleneck，如何解决，面试官的问题都回答上了，后期dive in主要着重于how to chunk large file in detail, get updated file list 的时候如何提高performance，get updated file list的时候有什么edge case吗，如何解决。面试官最后looking very good。
  12. 设计一个抢票系统
  13. trending hashtags: Top K 问题
  14. 设计post的隐私设置
  15. proximity service
  16. price tracker
  17. design camel camel camel
  18. Ticketmaster
  19. deep dive facebook news feed API 包括pagination.. 如何实现at一个人等
  20. design Spotify
  21. Design hotel booking system.
  22. 设计一个streaming service: 需要支持video play、recommendation、subscription
  23. Presence indicator
  24. 设计google map中，选择一个地点，可以拖拽看到周围街景的那个功能。主要问了问怎么hash longtitude/latitude，看看alex xu绿皮书Google map那一章会有帮助。‍‍‌‍‍‍‍‌‌‌‍‌‍‌‍‍‍‌‍‌以及如何降低latency，如何存储image等等。
  25. metrics monitoring
  26. youtube
  27. LeetCode contest platform

bq

  1. conflict with others, xfn conflict
  2. biggest mistake
  3. have you ever broke prod code
  4. most proud project
  5. difficult working re‍‍‌‍‍‍‍‌‌‌‍‌‍‌‍‍‍‌‍‌lationship
  6. conflict when you are right, conflict when you are wrong
  7. feedback from mana‍‍‌‍‍‍‍‌‌‌‍‌‍‌‍‍‍‌‍‌ger: negative feedback, critical feedback you received
  8. What did you learn from your tech lead, what do you want to improve?
  9. 多个task同时进行的时候怎么协调

Misc

lc339-Nested List Weight Sum

  • difficulty: Medium
  • tags:
    • Depth-First Search
    • Breadth-First Search

You are given a nested list of integers nestedList. Each element is either an integer or a list whose elements may also be integers or other lists.

The depth of an integer is the number of lists that it is inside of. For example, the nested list [1,[2,2],[[3],2],1] has each integer’s value set to its depth.

Return the sum of each integer in nestedList multiplied by its depth.

Example 1: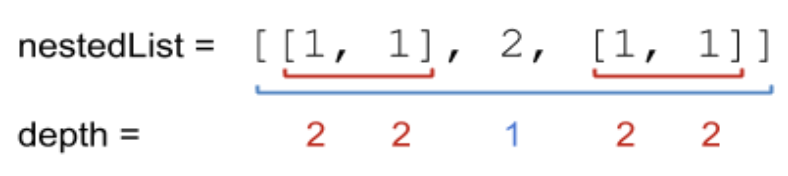
alt text

Input: nestedList = [[1,1],2,[1,1]]
Output: 10
Explanation: Four 1's at depth 2, one 2 at depth 1. 1*2 + 1*2 + 2*1 + 1*2 + 1*2 = 10.

Example 2: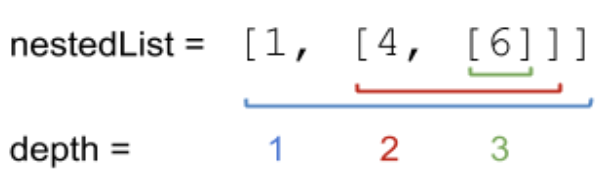
alt text

Input: nestedList = [1,[4,[6]]]
Output: 27
Explanation: One 1 at depth 1, one 4 at depth 2, and one 6 at depth 3. 1*1 + 4*2 + 6*3 = 27.

Example 3:

Input: nestedList = [0]
Output: 0

Constraints:

  • 1 <= nestedList.length <= 50
  • The values of the integers in the nested list is in the range [-100, 100].
  • The maximum depth of any integer is less than or equal to 50.

Solutions:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/**
 * // This is the interface that allows for creating nested lists.
 * // You should not implement it, or speculate about its implementation
 * public interface NestedInteger {
 *     // Constructor initializes an empty nested list.
 *     public NestedInteger();
 *
 *     // Constructor initializes a single integer.
 *     public NestedInteger(int value);
 *
 *     // @return true if this NestedInteger holds a single integer, rather than a nested list.
 *     public boolean isInteger();
 *
 *     // @return the single integer that this NestedInteger holds, if it holds a single integer
 *     // Return null if this NestedInteger holds a nested list
 *     public Integer getInteger();
 *
 *     // Set this NestedInteger to hold a single integer.
 *     public void setInteger(int value);
 *
 *     // Set this NestedInteger to hold a nested list and adds a nested integer to it.
 *     public void add(NestedInteger ni);
 *
 *     // @return the nested list that this NestedInteger holds, if it holds a nested list
 *     // Return empty list if this NestedInteger holds a single integer
 *     public List<NestedInteger> getList();
 * }
 */
class Solution {
    public int depthSum(List<NestedInteger> nestedList) {
        return dfs(nestedList, 1);
    }

    private int dfs(List<NestedInteger> nestedList, int depth) {
        int depthSum = 0;
        for (NestedInteger item : nestedList) {
            if (item.isInteger()) {
                depthSum += item.getInteger() * depth;
            } else {
                depthSum += dfs(item.getList(), depth + 1);
            }
        }
        return depthSum;
    }
}

Array

lc1762-Buildings With an Ocean View

  • difficulty: Medium
  • tags:
    • Stack
    • Array
    • Monotonic Stack

There are n buildings in a line. You are given an integer array heights of size n that represents the heights of the buildings in the line.

The ocean is to the right of the buildings. A building has an ocean view if the building can see the ocean without obstructions. Formally, a building has an ocean view if all the buildings to its right have a smaller height.

Return a list of indices (0-indexed) of buildings that have an ocean view, sorted in increasing order.

Example 1:

Input: heights = [4,2,3,1]
Output: [0,2,3]
Explanation: Building 1 (0-indexed) does not have an ocean view because building 2 is taller.

Example 2:

Input: heights = [4,3,2,1]
Output: [0,1,2,3]
Explanation: All the buildings have an ocean view.

Example 3:

Input: heights = [1,3,2,4]
Output: [3]
Explanation: Only building 3 has an ocean view.

Constraints:

  • 1 <= heights.length <= 105
  • 1 <= heights[i] <= 109

Solutions:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int[] findBuildings(int[] heights) {
        int n = heights.length;
        List<Integer> ans = new ArrayList<>();
        int mx = 0;
        for (int i = heights.length - 1; i >= 0; --i) {
            if (heights[i] > mx) {
                ans.add(i);
                mx = heights[i];
            }
        }
        Collections.reverse(ans);
        // return ans.stream().mapToInt(Integer::intValue).toArray();
        return ans.toArray(new int[0]);
    }
}

lc163-Missing Ranges

  • difficulty: Easy
  • tags:
    • Array

You are given an inclusive range [lower, upper] and a sorted unique integer array nums, where all elements are within the inclusive range.

A number x is considered missing if x is in the range [lower, upper] and x is not in nums.

Return the shortest sorted list of ranges that exactly covers all the missing numbers. That is, no element of nums is included in any of the ranges, and each missing number is covered by one of the ranges.

Example 1:

  • Input: nums = [0,1,3,50,75], lower = 0, upper = 99
  • Output: [[2,2],[4,49],[51,74],[76,99]]
  • Explanation: The ranges are:
    [2,2]
    [4,49]
    [51,74]
    [76,99]

Example 2:

  • Input: nums = [-1], lower = -1, upper = -1
  • Output: []
  • Explanation: There are no missing ranges since there are no missing numbers.

Constraints:

  • -109 <= lower <= upper <= 109
  • 0 <= nums.length <= 100
  • lower <= nums[i] <= upper
  • All the values of nums are unique.

We can simulate the problem directly according to the requirements.

The time complexity is O(n), where n is the length of the array nums. Ignoring the space consumption of the answer, the space complexity is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public List<List<Integer>> findMissingRanges(int[] nums, int lower, int upper) {
        int n = nums.length;
        if (n == 0) {
            return List.of(List.of(lower, upper));
        }
        List<List<Integer>> ans = new ArrayList<>();
        if (nums[0] > lower) {
            ans.add(List.of(lower, nums[0] - 1));
        }
        for (int i = 1; i < n; ++i) {
            if (nums[i] - nums[i - 1] > 1) {
                ans.add(List.of(nums[i - 1] + 1, nums[i] - 1));
            }
        }
        if (nums[n - 1] < upper) {
            ans.add(List.of(nums[n - 1] + 1, upper));
        }
        return ans;
    }
}

LinkedList

lc708-Insert into a Sorted Circular Linked List

Given a Circular Linked List node, which is sorted in non-descending order, write a function to insert a value insertVal into the list such that it remains a sorted circular list. The given node can be a reference to any single node in the list and may not necessarily be the smallest value in the circular list.

If there are multiple suitable places for insertion, you may choose any place to insert the new value. After the insertion, the circular list should remain sorted.

If the list is empty (i.e., the given node is null), you should create a new single circular list and return the reference to that single node. Otherwise, you should return the originally given node.

Example 1:

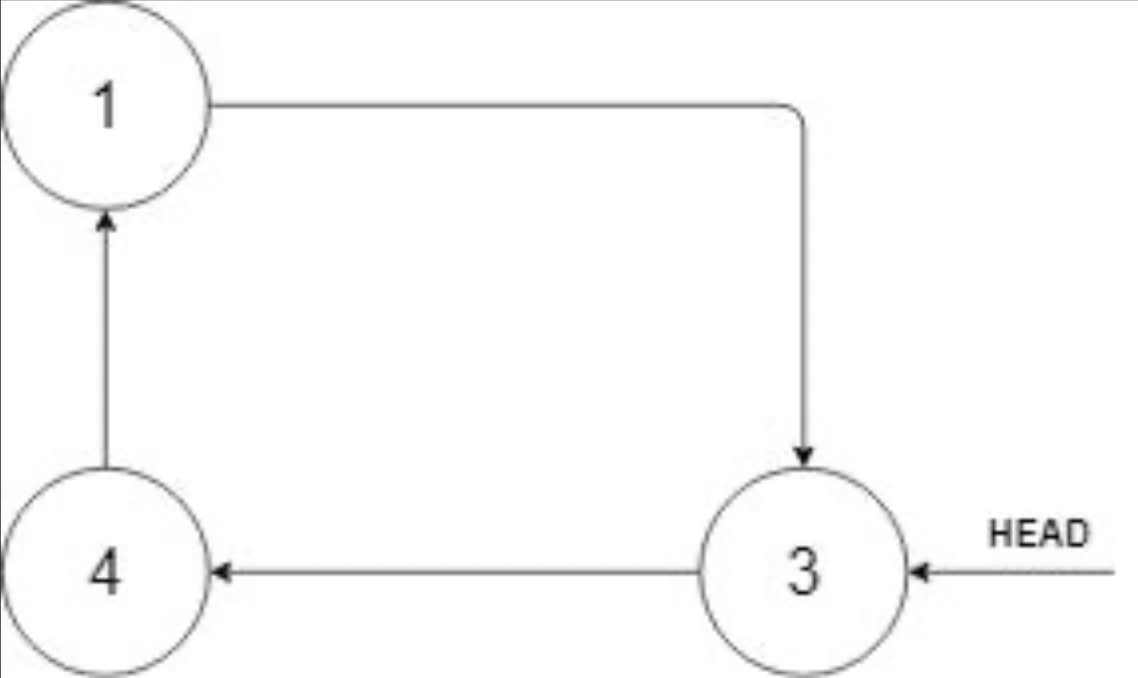
  • alt text
  • Input: head = [3,4,1], insertVal = 2
  • Output: [3,4,1,2]
  • Explanation: In the figure above, there is a sorted circular list of three elements. You are given a reference to the node with value 3, and we need to insert 2 into the list. The new node should be inserted between node 1 and node 3. After the insertion, the list should look like this, and we should still return node 3.
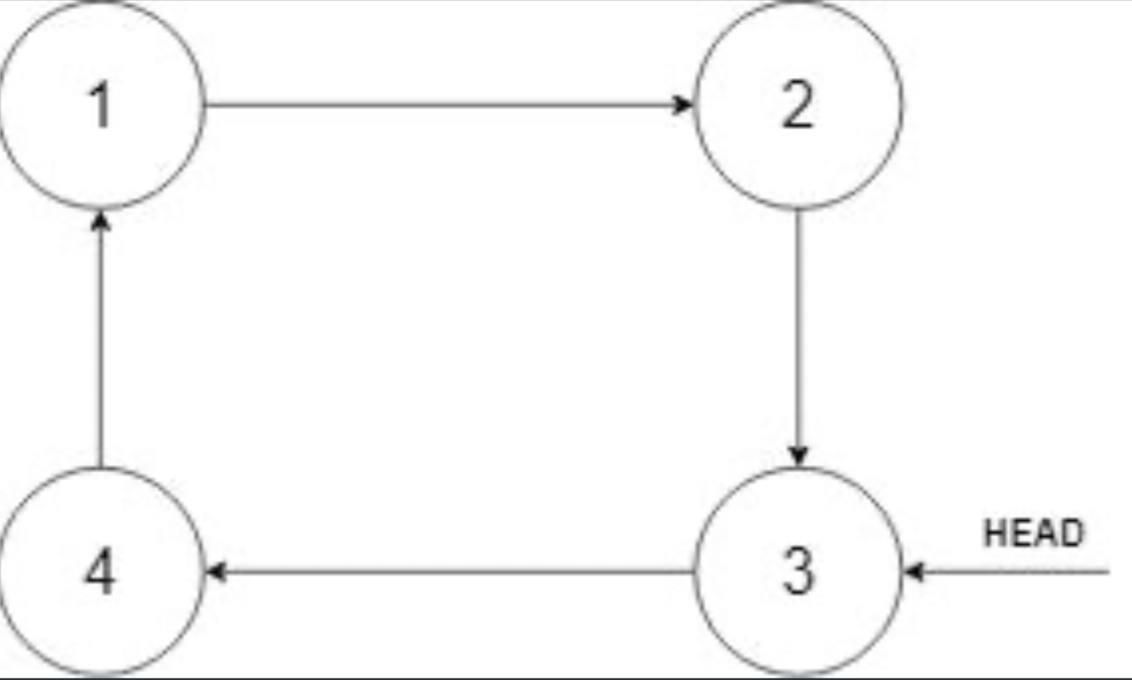
  • alt text

Example 2:

  • Input: head = [], insertVal = 1
  • Output: [1]
  • Explanation: The list is empty (given head is null). We create a new single circular list and return the reference to that single node.

Example 3:

  • Input: head = [1], insertVal = 0
  • Output: [1,0]

Constraints:

  • The number of nodes in the list is in the range [0, 5 * 104].
  • -106 <= Node.val, insertVal <= 106

Solutions

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/*
// Definition for a Node.
class Node {
    public int val;
    public Node next;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _next) {
        val = _val;
        next = _next;
    }
};
*/
class Solution {
    public Node insert(Node head, int insertVal) {
        Node node = new Node(insertVal);
        if (head == null) {
            node.next = node;
            return node;
        }
        Node prev = head, curr = head.next;
        while (curr != head) {
            if (prev.val <= insertVal && insertVal <= curr.val) {
                  break;  // 插入值在 current 和 current.next 之间
            }
            if (prev.val > curr.val) {  // pre是最大值, curr是最小值, 因为是从小到大遍历, prev > curr说明遍历到头了
                if (insertVal >= prev.val || insertVal <= curr.val) {
                    break;  // 插入值大于最大值或小于最小值的情况
                }
            }
            prev = curr;
            curr = curr.next;
        }
        prev.next = node;
        node.next = curr;
        return head;
    }
}

HashMap

lc266-Palindrome Permutation

  • difficulty: Easy
  • tags:
    • Bit Manipulation
    • Hash Table
    • String

Given a string s, return true if a permutation of the string could form a palindrome and false otherwise.

Example 1:

  • Input: s = “code”
  • Output: false

Example 2:

  • Input: s = “aab”
  • Output: true

Example 3:

  • Input: s = “carerac”
  • Output: true

Constraints:

  • 1 <= s.length <= 5000
  • s consists of only lowercase English letters.

Solutions:

If a string is a palindrome, at most one character can appear an odd number of times, while all other characters must appear an even number of times. Therefore, we only need to count the occurrences of each character and then check if this condition is satisfied.

Time complexity is O(n), and space complexity is O(|\Sigma|). Here, n is the length of the string, and |\Sigma| is the size of the character set. In this problem, the character set consists of lowercase letters, so |\Sigma|=26.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public boolean canPermutePalindrome(String s) {
        HashMap<Character, Integer> countMap = new HashMap<>();
        
        // Count frequency of each character
        for (char c : s.toCharArray()) {
            countMap.put(c, countMap.getOrDefault(c, 0) + 1);
        }
        
        // Check how many characters have an odd frequency
        int oddCount = 0;
        for (int count : countMap.values()) {
            if (count % 2 != 0) {
                oddCount++;
            }
            // If more than one character has an odd count, return false
            if (oddCount > 1) {
                return false;
            }
        }
        
        return true;
    }
}

lc249-Group Shifted Strings

Perform the following shift operations on a string:

Right shift: Replace every letter with the successive letter of the English alphabet, where 'z' is replaced by 'a'. For example, "abc" can be right-shifted to "bcd" or "xyz" can be right-shifted to "yza".
Left shift: Replace every letter with the preceding letter of the English alphabet, where 'a' is replaced by 'z'. For example, "bcd" can be left-shifted to "abc" or "yza" can be left-shifted to "xyz".
We can keep shifting the string in both directions to form an endless shifting sequence.

For example, shift "abc" to form the sequence: … <-> "abc" <-> "bcd" <-> … <-> "xyz" <-> "yza" <-> …. <-> "zab" <-> "abc" <-> …
You are given an array of strings strings, group together all strings[i] that belong to the same shifting sequence. You may return the answer in any order.

Example 1:

Input: strings = ["abc","bcd","acef","xyz","az","ba","a","z"]
Output: [["acef"],["a","z"],["abc","bcd","xyz"],["az","ba"]]
Explanation: "az" can be left-shifted to "ba"

Example 2:

Input: strings = ["a"]
Output: [["a"]]

Constraints:

  • 1 <= strings.length <= 200
  • 1 <= strings[i].length <= 50
  • strings[i] consists of lowercase English letters.

Solutions:

We use a hash table g to store each string after shifting and with the first character as ‘a‘. That is, g[t] represents the set of all strings that become t after shifting.

We iterate through each string. For each string, we calculate its shifted string t, and then add it to g[t].

Finally, we take out all the values in g, which is the answer.

The time complexity is O(L) and the space complexity is O(L), where L is the sum of the lengths of all strings.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public List<List<String>> groupStrings(String[] strings) {
        Map<String, List<String>> g = new HashMap<>();
        for (var s : strings) {
            char[] t = s.toCharArray();
            int diff = t[0] - 'a';
            for (int i = 0; i < t.length; ++i) {
                t[i] = (char) (t[i] - diff);
                if (t[i] < 'a') {
                    t[i] += 26;
                }
            }
            g.computeIfAbsent(new String(t), k -> new ArrayList<>()).add(s);
        }
        return new ArrayList<>(g.values());
    }
}

lc1570-Dot Product of Two Sparse Vectors

  • difficulty: Medium
  • tags:
    • Design
    • Array
    • Hash Table
    • Two Pointers

Given two sparse vectors, compute their dot product.

Implement class SparseVector:

SparseVector(nums) Initializes the object with the vector nums
dotProduct(vec)Compute the dot product between the instance of SparseVector and vec
A sparse vector is a vector that has mostly zero values, you should store the sparse vector efficiently and compute the dot product between two SparseVector.

Follow up: What if only one of the vectors is sparse?

Example 1:

Input: nums1 = [1,0,0,2,3], nums2 = [0,3,0,4,0]
Output: 8
Explanation: v1 = SparseVector(nums1) , v2 = SparseVector(nums2)
v1.dotProduct(v2) = 1*0 + 0*3 + 0*0 + 2*4 + 3*0 = 8

Example 2:

Input: nums1 = [0,1,0,0,0], nums2 = [0,0,0,0,2]
Output: 0
Explanation: v1 = SparseVector(nums1) , v2 = SparseVector(nums2)
v1.dotProduct(v2) = 0*0 + 1*0 + 0*0 + 0*0 + 0*2 = 0

Example 3:

Input: nums1 = [0,1,0,0,2,0,0], nums2 = [1,0,0,0,3,0,4]
Output: 6

Constraints:

  • n == nums1.length == nums2.length
  • 1 <= n <= 10^5
  • 0 <= nums1[i], nums2[i] <= 100

Solutions: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class SparseVector {
    public Map<Integer, Integer> d = new HashMap<>(128);

    SparseVector(int[] nums) {
        for (int i = 0; i < nums.length; ++i) {
            // A sparse vector is a vector that has mostly zero values, you should store the sparse vector efficiently and compute the dot product between two SparseVector.
            if (nums[i] != 0) {
                d.put(i, nums[i]);
            }
        }
    }

    // Return the dotProduct of two sparse vectors
    public int dotProduct(SparseVector vec) {
        var a = d;
        var b = vec.d;
        if (b.size() < a.size()) {
            var t = a;
            a = b;
            b = t;
        }
        int ans = 0;
        for (var e : a.entrySet()) {
            int i = e.getKey(), v = e.getValue();
            ans += v * b.getOrDefault(i, 0);
        }
        return ans;
    }
}

// Your SparseVector object will be instantiated and called as such:
// SparseVector v1 = new SparseVector(nums1);
// SparseVector v2 = new SparseVector(nums2);
// int ans = v1.dotProduct(v2);

Queue

lc346-Moving Average from Data Stream

  • difficulty: Easy
  • tags:
    • Design
    • Queue
    • Array
    • Data Stream

Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.

Implement the MovingAverage class:

MovingAverage(int size) Initializes the object with the size of the window size.
double next(int val) Returns the moving average of the last size values of the stream.

Example 1:

Input:
["MovingAverage", "next", "next", "next", "next"]
[[3], [1], [10], [3], [5]]

Output:
[null, 1.0, 5.5, 4.66667, 6.0]

Explanation:
MovingAverage movingAverage = new MovingAverage(3);
movingAverage.next(1); // return 1.0 = 1 / 1
movingAverage.next(10); // return 5.5 = (1 + 10) / 2
movingAverage.next(3); // return 4.66667 = (1 + 10 + 3) / 3
movingAverage.next(5); // return 6.0 = (10 + 3 + 5) / 3

Constraints:

  • 1 <= size <= 1000
  • -105 <= val <= 105
  • At most 104 calls will be made to next.

Solution:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class MovingAverage {
    private Deque<Integer> q = new ArrayDeque<>();
    private int n;
    private int s;

    public MovingAverage(int size) {
        n = size;
    }

    public double next(int val) {
        if (q.size() == n) {
            s -= q.pollFirst();
        }
        q.offer(val);
        s += val;
        return s * 1.0 / q.size();
    }
}
/**
 * Your MovingAverage object will be instantiated and called as such:
 * MovingAverage obj = new MovingAverage(size);
 * double param_1 = obj.next(val);
 */

String

lc408-Valid Word Abbreviation

A string can be abbreviated by replacing any number of non-adjacent, non-empty substrings with their lengths. The lengths should not have leading zeros.

For example, a string such as “substitution” could be abbreviated as (but not limited to):

  • “s10n” (“s ubstitutio n”)
  • “sub4u4” (“sub stit u tion”)
  • “12” (“substitution”)
  • “su3i1u2on” (“su bst i t u ti on”)
  • “substitution” (no substrings replaced)

The following are not valid abbreviations:

  • “s55n” (“s ubsti tutio n”, the replaced substrings are adjacent)
  • “s010n” (has leading zeros)
  • “s0ubstitution” (replaces an empty substring)

Given a string word and an abbreviation abbr, return whether the string matches the given abbreviation.

A substring is a contiguous non-empty sequence of characters within a string.

Example 1:

Input: word = "internationalization", abbr = "i12iz4n"
Output: true
Explanation: The word "internationalization" can be abbreviated as "i12iz4n" ("i nternational iz atio n").

Example 2:

Input: word = "apple", abbr = "a2e"
Output: false
Explanation: The word "apple" cannot be abbreviated as "a2e".

Constraints:

  • 1 <= word.length <= 20
  • word consists of only lowercase English letters.
  • 1 <= abbr.length <= 10
  • abbr consists of lowercase English letters and digits.
  • All the integers in abbr will fit in a 32-bit integer.

Solution 1:

We can directly simulate character matching and replacement.

Assume the lengths of the string word and the string abbr are m and n respectively. We use two pointers i and j to point to the initial positions of the string word and the string abbr respectively, and use an integer variable x to record the current matched number in abbr.

Loop to match each character of the string word and the string abbr:

If the character abbr[j] pointed by the pointer j is a number, if abbr[j] is '0' and x is 0, it means that the number in abbr has leading zeros, so it is not a valid abbreviation, return false; otherwise, update x to x * 10 + abbr[j] - '0'.

If the character abbr[j] pointed by the pointer j is not a number, then we move the pointer i forward by x positions at this time, and then reset x to 0. If i greater than or equal to m or word[i] is not equal to abbr[j] at this time, it means that the two strings cannot match, return false; otherwise, move the pointer i forward by 1 position.

Then we move the pointer j forward by 1 position, repeat the above process, until i exceeds the length of the string word or j exceeds the length of the string abbr.

Finally, if i + x equals m and j equals n, it means that the string word can be abbreviated as the string abbr, return true; otherwise return false.

The time complexity is O(m + n), where m and n are the lengths of the string word and the string abbr respectively. The space complexity is O(1).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public boolean validWordAbbreviation(String word, String abbr) {
        int m = word.length(), n = abbr.length();
        int i = 0, j = 0, x = 0;
        for (; i < m && j < n; ++j) {
            char c = abbr.charAt(j);
            if (Character.isDigit(c)) {
                if (c == '0' && x == 0) {
                    return false;
                }
                x = x * 10 + (c - '0');
            } else {
                i += x;
                x = 0;
                if (i >= m || word.charAt(i) != c) {
                    return false;
                }
                ++i;
            }
        }
        return i + x == m && j == n;
    }
}

Binary Tree

lc1650-Lowest Common Ancestor of a Binary Tree III

Description:

Given two nodes of a binary tree p and q, return their lowest common ancestor (LCA).

Each node will have a reference to its parent node. The definition for Node is below:

1
2
3
4
5
6
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node parent;
}

According to the definition of LCA on Wikipedia: “The lowest common ancestor of two nodes p and q in a tree T is the lowest node that has both p and q as descendants (where we allow a node to be a descendant of itself).”

Example 1: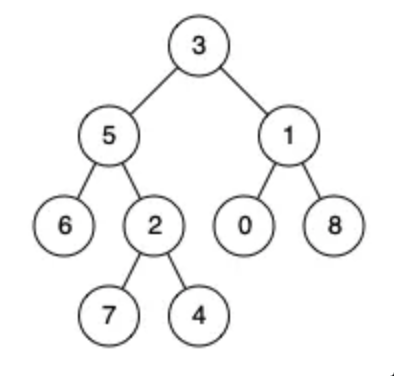
alt text

1
2
3
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
Output: 3
Explanation: The LCA of nodes 5 and 1 is 3.

Example 2: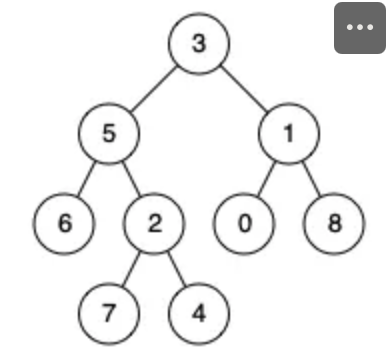
alt text

1
2
3
Input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
Output: 5
Explanation: The LCA of nodes 5 and 4 is 5 since a node can be a descendant of itself according to the LCA definition.

Example 3:

1
2
Input: root = [1,2], p = 1, q = 2
Output: 1

Constraints:

  • The number of nodes in the tree is in the range [2, 105].
  • 109 <= Node.val <= 109
  • All Node.val are unique.
  • p != q
  • p and q exist in the tree.

Solution: 

1
2
3
4
5
6
7
8
9
10
// - 其实就变成求两条链表的相交点了, refer to : https://programmercarl.com/面试题02.07.链表相交.html#其他语言版本
// - Two runners and circle track,  same as leetcode-160: https://leetcode.com/problems/intersection-of-two-linked-lists/description/
public Node lowestCommonAncestor(Node p, Node q) {
	Node a = p, b = q;
	while (a != b) {
		a = a == null? q : a.parent;
		b = b == null? p : b.parent;    
	}
	return a;
}

DFS

BFS

lc314-lc987-Binary Tree vertical order traversal

Given the root of a binary tree, return the vertical order traversal of its nodes’ values. (i.e., from top to bottom, column by column).

If two nodes are in the same row and column, the order should be from left to right.

Example 1:

Input: root = [3,9,20,null,null,15,7]
Output: [[9],[3,15],[20],[7]]
Example 2:

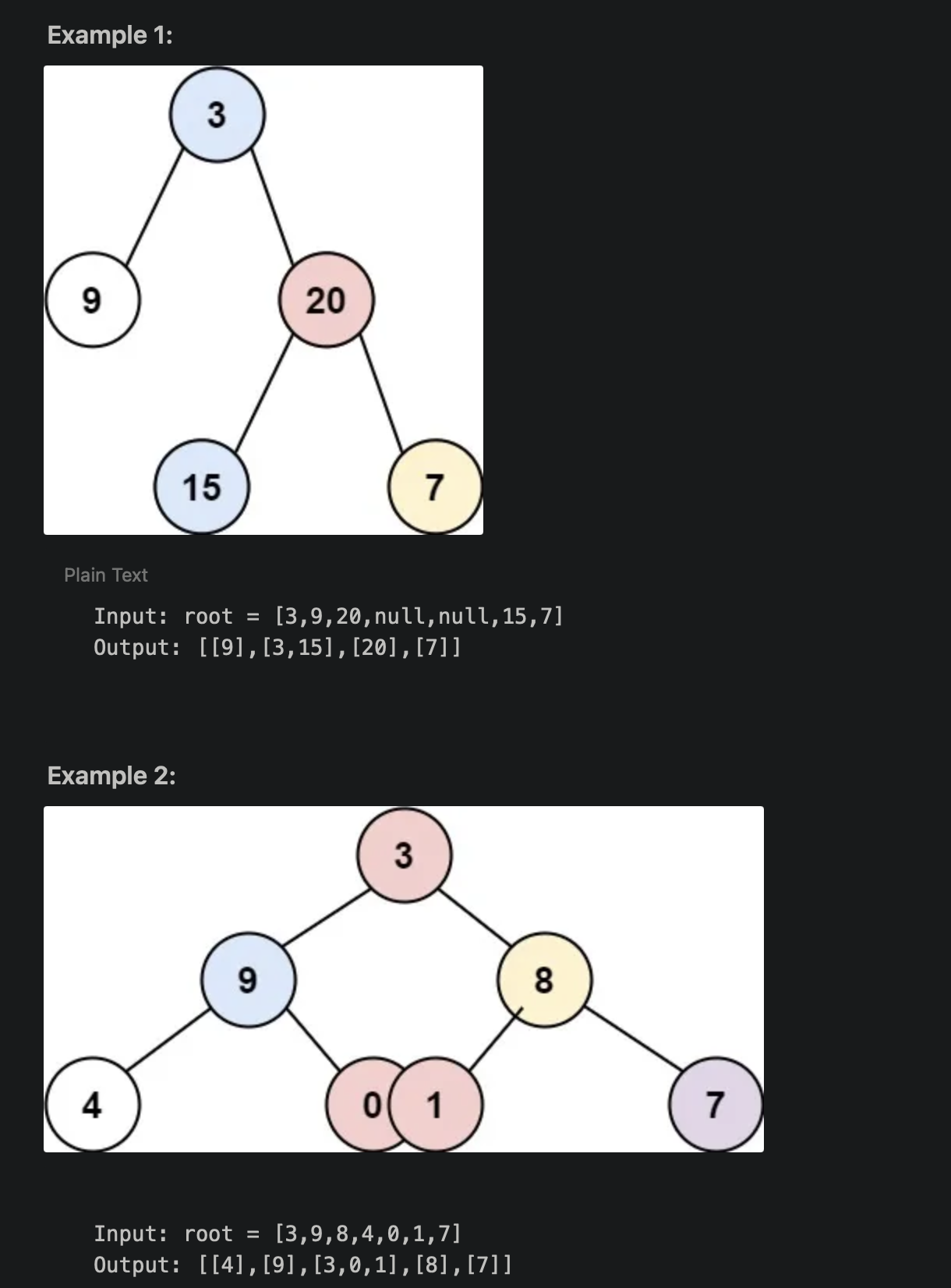
Input: root = [3,9,8,4,0,1,7]
Output: [[4],[9],[3,0,1],[8],[7]]
Example 3:

Input: root = [3,9,8,4,0,1,7,null,null,null,2,5]
Output: [[4],[9,5],[3,0,1],[8,2],[7]]

alt text

Constraints:

The number of nodes in the tree is in the range [0, 100].
-100 <= Node.val <= 100

Solution1: (最优解, 而且最好理解, 还方便对于同行同列的值排序, 参见LC987)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution {
    public static List<List<Integer>> verticalTraversal(TreeNode root) {
        List<List<Integer>> resultList = new ArrayList<>();
        if (root == null) {
            return resultList;
        }

        List<int[]> nodes = new ArrayList<>();
        int row = 0;
        Queue<TreeNode> nodeQueue = new ArrayDeque<>();
        Queue<Integer> colQueue = new ArrayDeque<>();

        nodeQueue.offer(root);
        colQueue.offer(0);

        while (!nodeQueue.isEmpty()) {
            int len = nodeQueue.size();
            row++;
            while (len > 0) {
                TreeNode tempNode = nodeQueue.poll();
                int curCol = colQueue.poll();
                nodes.add(new int[]{curCol, row, tempNode.val});  // 注意是先col再row再value, 不是先row再col
                // add children for level order traversal
                if (tempNode.left != null) {
                    nodeQueue.offer(tempNode.left);
                    colQueue.offer(curCol - 1);
                }
                if (tempNode.right != null) {
                    nodeQueue.offer(tempNode.right);
                    colQueue.offer(curCol + 1);
                }
                len--;
            }
        }

        // 如果要对于同行同列的值排序, 就取消下面这几行代码的注释
        // Sort nodes by column, row, and value
        // Collections.sort(nodes, (tuple1, tuple2) -> {
        //     if (tuple1[0] != tuple2[0]) {
        //         return tuple1[0] - tuple2[0];
        //     } else if (tuple1[1] != tuple2[1]) {
        //         return tuple1[1] - tuple2[1];
        //     } else {
        //         return tuple1[2] - tuple2[2];
        //     }
        // });


        int lastCol = Integer.MIN_VALUE;
        for (int[] node : nodes) {
            // System.out.println(Arrays.toString(node));
            int nodeCol = node[0];
            int nodeVal = node[2];
            if (nodeCol != lastCol) {
                List<Integer> newArray = new ArrayList<>();
                resultList.add(newArray);
                lastCol = nodeCol;
            }
            resultList.get(resultList.size() - 1).add(nodeVal);
        }

        return resultList;
    }
}

Solution2: (这个解法还适合用来解”top/bottom view of binary tree”, 但是无法处理LC987的’对同行同列的值排序’这种情况, 因为 colToVals 这个 map只存了col信息, 无法排序)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
// - BFS level order traversal, time O(N), space O(N)
    
//     Observation:
    
//     - The column range is continuous, from min to max
    
//     Steps
    
//     - BFS, put `node`, `col` into queue at the same time
//     - Every left child access `col - 1` while right child `col + 1`
//     - This maps `node` into different `col` buckets
//     - Get `col` boundary `min` and `max` on the fly
//     - Retrieve `result` from `cols`

import java.util.Map;
import java.util.Queue;
import java.util.Collections;
import java.util.HashMap;
import java.util.LinkedList;
import java.util.List;
import java.util.Arrays;
import java.util.ArrayList;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {}
    TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

class Solution {

    public static List<List<Integer>> verticalOrder(TreeNode root) {
        List<List<Integer>> resultList = new ArrayList<>();
        if (root == null) {
            return resultList;
        }

        Map<Integer, List<Integer>> colToVals = new HashMap<>();
        Queue<TreeNode> nodeQueue = new ArrayDeque<>();
        Queue<Integer> colQueue = new ArrayDeque<>();
        nodeQueue.offer(root);
        colQueue.offer(0);

        int minColIndex = 0;
        int maxColIndex = 0;
        while (!nodeQueue.isEmpty()) {
            int len = nodeQueue.size();
            while (len > 0) {
                TreeNode tempNode = nodeQueue.poll();
                int curCol = colQueue.poll();

                if (colToVals.containsKey(curCol)) {
                    List<Integer> curVals = colToVals.get(curCol);
                    curVals.add(tempNode.val);
                } else {
                    List<Integer> newVals = new ArrayList<>();
                    newVals.add(tempNode.val);
                    colToVals.put(curCol, newVals);
                }

                // update min, max cols and add current value to corresponding column's list
                minColIndex = Math.min(curCol, minColIndex);
                maxColIndex = Math.max(curCol, maxColIndex);

                // add children for level order traversal
                if (tempNode.left != null) {
                    nodeQueue.offer(tempNode.left);
                    colQueue.offer(curCol - 1);
                }
                if (tempNode.right != null) {
                    nodeQueue.offer(tempNode.right);
                    colQueue.offer(curCol + 1);
                }
                len--;
            }
        }

        // build result
        for (int i = minColIndex; i <= maxColIndex; i++) {
            resultList.add(colToVals.get(i));
        }

        return resultList;
    }

    public static void main(String[] args) {
        TreeNode testTree = new TreeNode(3);
        testTree.left = new TreeNode(9);
        testTree.right = new TreeNode(20);
        testTree.right.left = new TreeNode(15);
        testTree.right.right = new TreeNode(7);
        List<List<Integer>> result = verticalOrder(testTree);
        System.out.println(result);

    }
}

Solution 3: (不推荐, 但是一种思路)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    public List<List<Integer>> verticalTraversal(TreeNode root) {
        // List to store nodes with their column, row, and value
        List<int[]> nodes = new ArrayList<>();
        
        // Perform DFS traversal
        dfs(root, 0, 0, nodes);
        
        // 如果要对于同行同列的值排序, 就取消下面这几行代码的注释
        // // Sort nodes by column, row, and value
        // // 1. 
        // Collections.sort(nodes, (tuple1, tuple2) -> {
        // // 2. 
        // // Collections.sort(nodes, new Comparator<int[]>() {
        //     // public int compare(int[] tuple1, int[] tuple2) {
        // // 3. 
        // // Collections.sort(nodes, (int[] tuple1, int[] tuple2) -> {
        //     if (tuple1[0] != tuple2[0]) {
        //         return tuple1[0] - tuple2[0];
        //     } else if (tuple1[1] != tuple2[1]) {
        //         return tuple1[1] - tuple2[1];
        //     } else {
        //         return tuple1[2] - tuple2[2];
        //     }
        // });
        
        // List to store the final result (list of lists for each column)
        List<List<Integer>> ans = new ArrayList<>();
        
        // Variable to track the last column seen
        int lastcol = Integer.MIN_VALUE;
        
        // Iterate over sorted nodes and group by column
        for (int[] tuple : nodes) {
            int col = tuple[0], row = tuple[1], value = tuple[2];
            if (col != lastcol) {
                lastcol = col;
                ans.add(new ArrayList<>());
            }
            ans.get(ans.size() - 1).add(value);
        }
        
        return ans;
    }

    // DFS method to traverse the tree and collect nodes with (col, row, value)
    public void dfs(TreeNode node, int row, int col, List<int[]> nodes) {
        if (node == null) {
            return;
        }
        
        nodes.add(new int[]{col, row, node.val});
        dfs(node.left, row + 1, col - 1, nodes);
        dfs(node.right, row + 1, col + 1, nodes);
    }
}

lc199-Binary Tree Right Side View

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        List<Integer> resultList = new ArrayList<Integer>();
        if (root == null ) {
            return resultList;
        }
        Queue<TreeNode> que = new LinkedList<TreeNode>();
        que.offer(root);

        while (!que.isEmpty()) {
            int len = que.size();
            while (len > 0) {  // 注意这个len, 这里一定要使用固定大小 len，不要使用que.size()，因为que.size是不断变化的
                TreeNode tmpNode = que.poll();
                if (len == 1) {
                    // 层序遍历的时候，判断是否遍历到单层的最后面的元素，如果是，就放进result数组中，随后返回result就可以了。
                    resultList.add(tmpNode.val);
                }

                if (tmpNode.left != null) { que.offer(tmpNode.left); }
                if (tmpNode.right != null) { que.offer(tmpNode.right); }
                len--;
            }
        }

        return resultList;
    }
}

lc543-diameter-of-binary-tree

BST

lc938-range-sum-of-bst

lc426-Convert Binary Search Tree to Sorted Doubly Linked List

Convert a Binary Search Tree to a sorted Circular Doubly-Linked List in place.

You can think of the left and right pointers as synonymous to the predecessor and successor pointers in a doubly-linked list. For a circular doubly linked list, the predecessor of the first element is the last element, and the successor of the last element is the first element.

We want to do the transformation in place. After the transformation, the left pointer of the tree node should point to its predecessor, and the right pointer should point to its successor. You should return the pointer to the smallest element of the linked list.

Example 1:

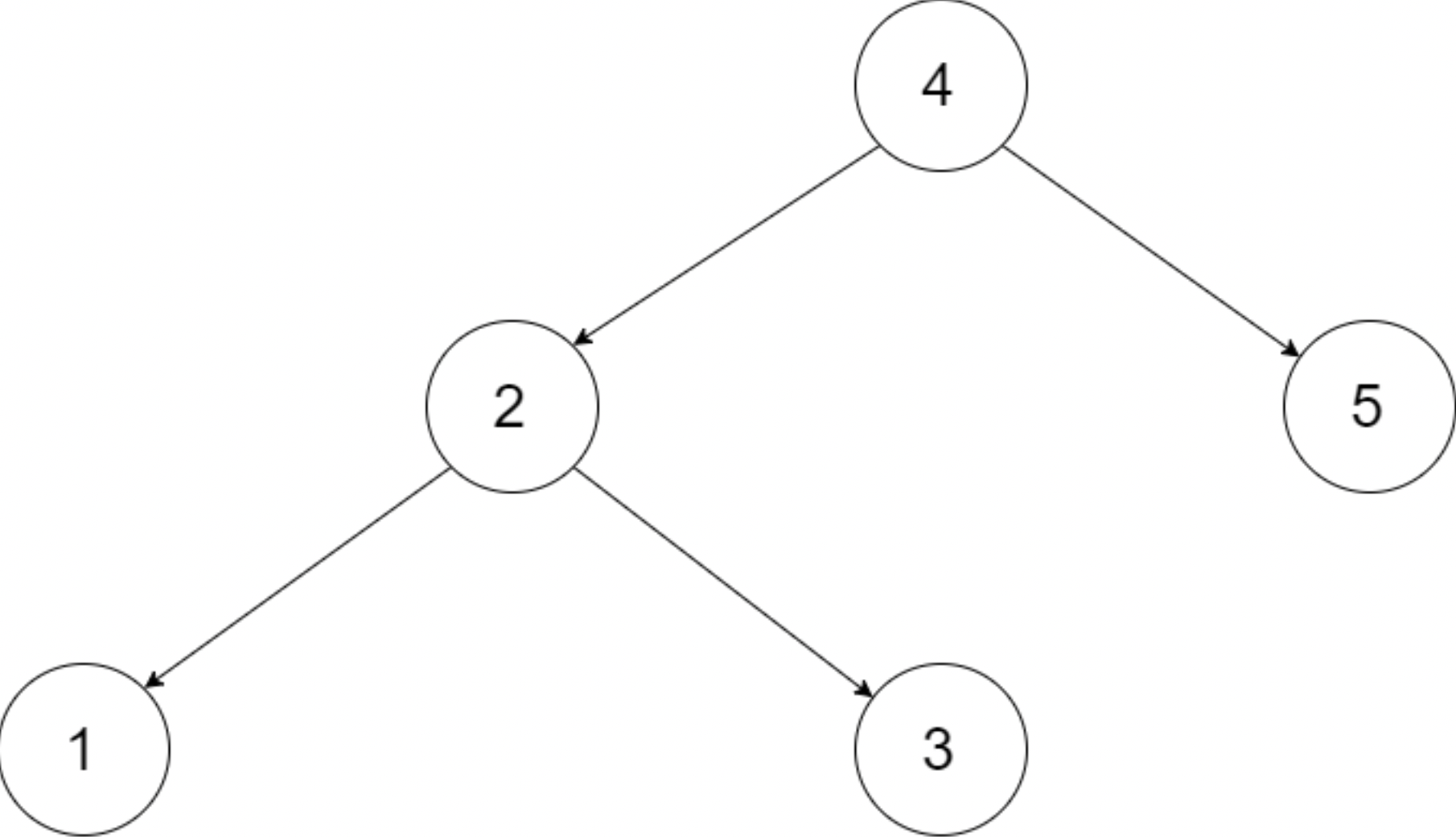
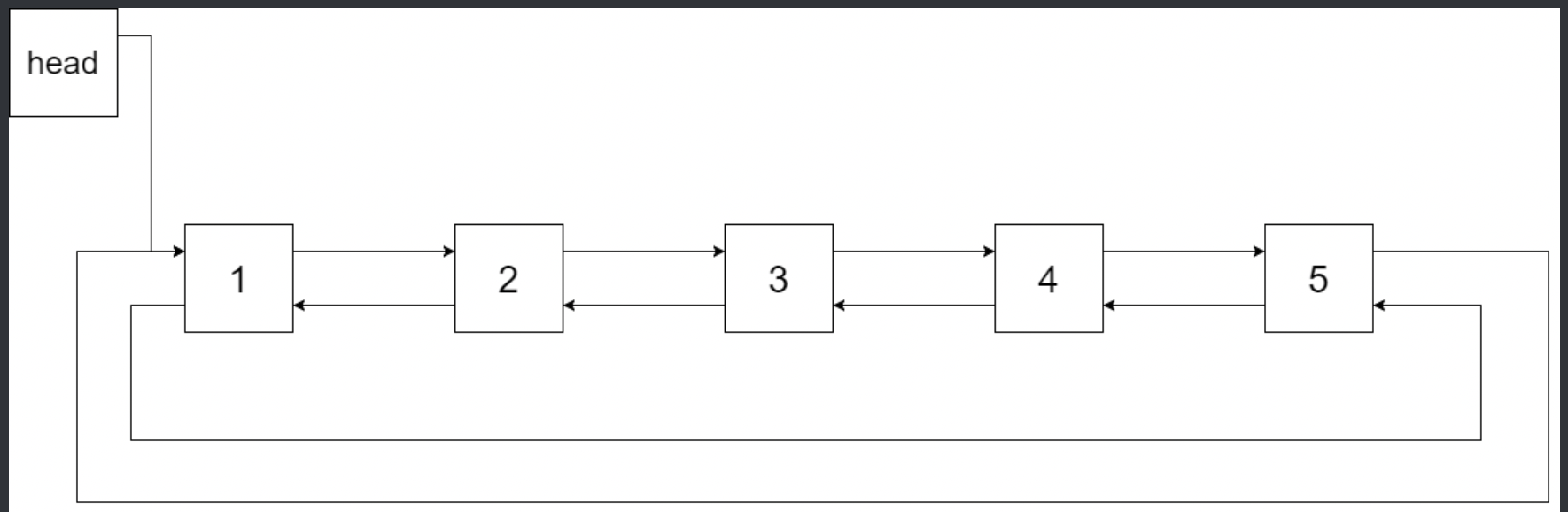
  • alt text
  • alt text
  • Input: root = [4,2,5,1,3]
  • Output: [1,2,3,4,5]
  • Explanation: The figure below shows the transformed BST. The solid line indicates the successor relationship, while the dashed line means the predecessor relationship.
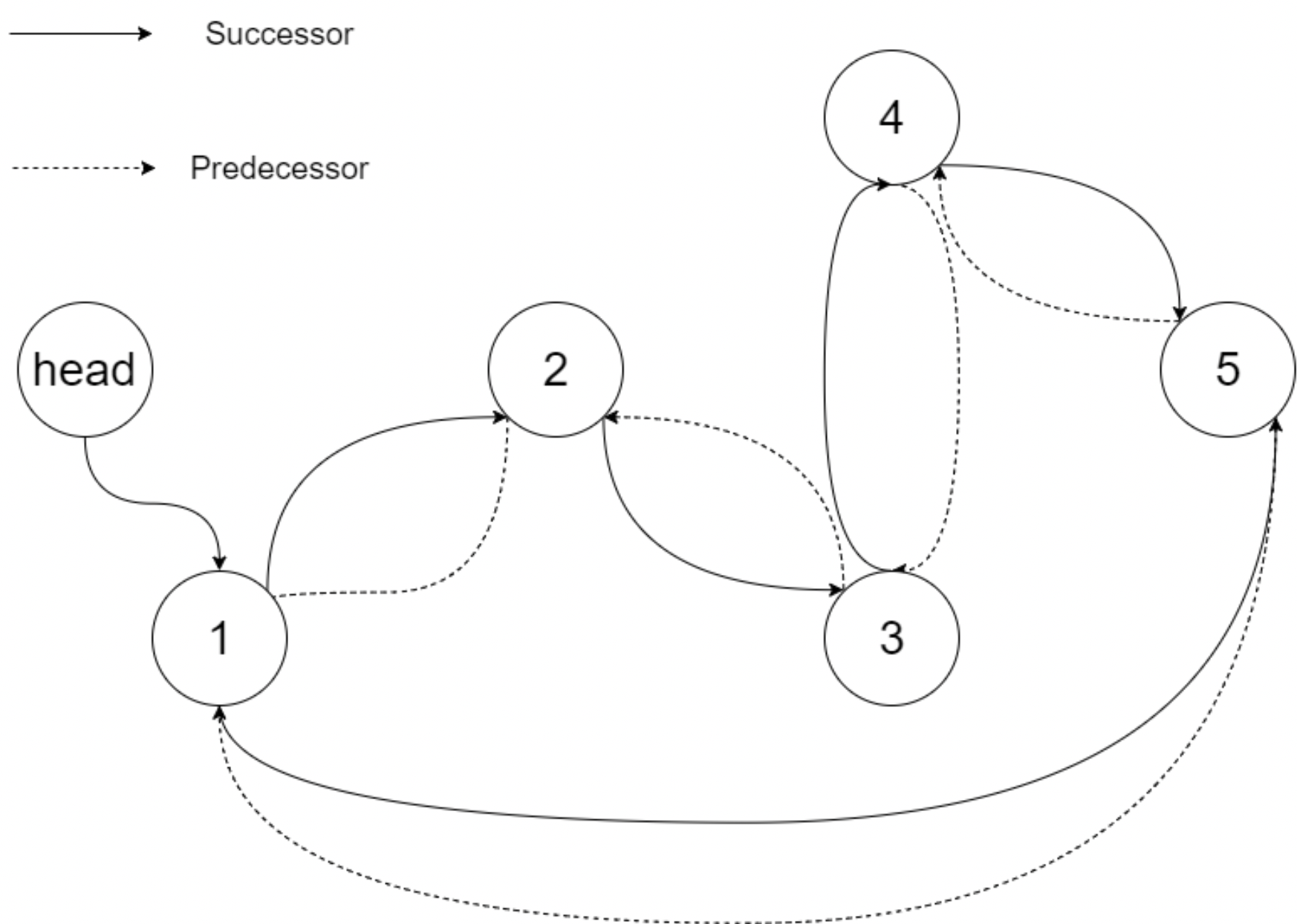
  • alt text

Example 2:

  • Input: root = [2,1,3]
  • Output: [1,2,3]

Constraints:

  • The number of nodes in the tree is in the range [0, 2000].
  • -1000 <= Node.val <= 1000
  • All the values of the tree are unique.

Solution: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
    private Node prev;
    private Node head;

    public Node treeToDoublyList(Node root) {
        if (root == null) {
            return null;
        }
        prev = null;
        head = null;
        dfs(root);
        prev.right = head;
        head.left = prev;
        return head;
    }

    private void dfs(Node root) {
        // Since an in-order traversal of a binary search tree gives us a sorted array,
        if (root == null) {
            return;
        }
        dfs(root.left);
        if (prev != null) {
            prev.right = root;
            root.left = prev;
        } else {
            head = root;
        }
        prev = root;
        dfs(root.right);
    }
}

lc270-Closest Binary Search Tree Value

Given the root of a binary search tree and a target value, return the value in the BST that is closest to the target. If there are multiple answers, print the smallest.

Example 1:

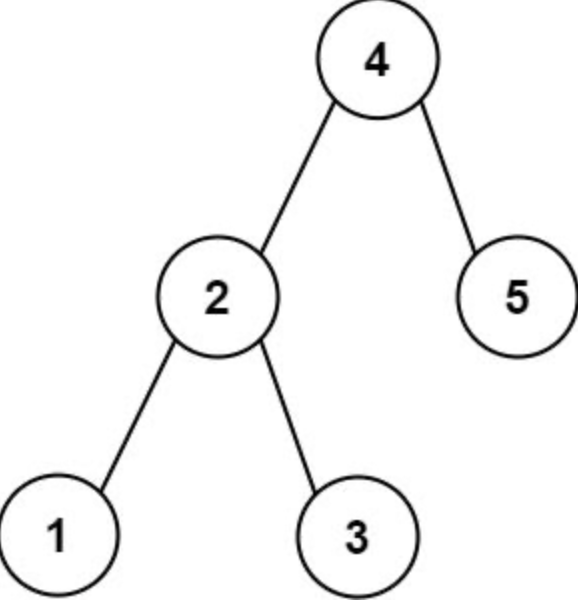
  • alt text
  • Input: root = [4,2,5,1,3], target = 3.714286
  • Output: 4

Example 2:

  • Input: root = [1], target = 4.428571
  • Output: 1

Constraints:

  • The number of nodes in the tree is in the range [1, 104].
  • 0 <= Node.val <= 109
  • -109 <= target <= 109

Solution 1: Recursion

We define a recursive function dfs(node), which starts from the current node node and finds the node closest to the target value target. We can update the answer by comparing the absolute difference between the current node’s value and the target value. If the target value is less than the current node’s value, we recursively search the left subtree; otherwise, we recursively search the right subtree.

The time complexity is O(n), and the space complexity is O(n). Where n is the number of nodes in the binary search tree.

Recursion
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    private int ans;
    private double target;
    private double diff = Double.MAX_VALUE;

    public int closestValue(TreeNode root, double target) {
        this.target = target;
        dfs(root);
        return ans;
    }

    private void dfs(TreeNode node) {
        if (node == null) {
            return;
        }
        double nxt = Math.abs(node.val - target);
        if (nxt < diff || (nxt == diff && node.val < ans)) {
            diff = nxt;
            ans = node.val;
        }
        node = target < node.val ? node.left : node.right;
        dfs(node);
    }
}

Solution 2: Iteration

We can rewrite the recursive function in an iterative form, using a loop to simulate the recursive process. We start from the root node and check whether the absolute difference between the current node’s value and the target value is less than the current minimum difference. If it is, we update the answer. Then, based on the size relationship between the target value and the current node’s value, we decide to move to the left subtree or the right subtree. The loop ends when we traverse to a null node.

The time complexity is O(n), where n is the number of nodes in the binary search tree. The space complexity is O(1).

Iteration
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public int closestValue(TreeNode root, double target) {
        int ans = root.val;
        double diff = Double.MAX_VALUE;
        while (root != null) {
            double nxt = Math.abs(root.val - target);
            if (nxt < diff || (nxt == diff && root.val < ans)) {
                diff = nxt;
                ans = root.val;
            }
            root = target < root.val ? root.left : root.right;
        }
        return ans;
    }
}