NA Algo Tricks

Posted on | In

算法白话总结

. . .

找工小队群里公司面经

  • hong:
    • 华人Wevision旗下小创业公司
      • algo: 岛屿大小LC695, LC621，LC127, LC934
      1. 第一轮就一个算法题：岛屿大小，然后聊了点项目和简历
      2. 第二轮两个算法题：LC621，LC127
      3. 第三轮一个算法一个SD：LC934，短链服务
      4. 第四轮两个SD: 设计一个数据平台，设计一个消息通知系统
  • nao:
    • DoorDash:
      • DoorDash问的leetcode 124的变种 是他家高频面经, doordash的sd也是他家高频面经 设计一个评论系统, 其实不难 你提前做一做, 研究透了就行
      • algo: 124,
      • sd: 设计一个评论系统
    • databricks:
      • databricks都是面经 题目比较复杂 这里说不清, databricks就是纯面经题库 很容易押到题, databricks的问题就是你押中原题了 也不一定能做得好 因为太难了
    • Walmart:
      • algo:
        • next permutation(题号lc31, 经典题),
        • lc68,
        • 写一个二叉搜索树, 能实现加节点和删除节点
        • 另一个给出每张图片需要处理的起始天和终点天[start, end],和每张图片处理一天需要的花费，n张图片，每天处理的总花费如果超过x，总花费就视为x，求处理所有图片的最少花费 不是lc原题 是hackerrank上的题目
      • 第一轮: lc68，先是一个简单版的 然后才是68本体，没写完本体 也给过了, 第一轮还问了一些k8s的八股 完全不会 也给过了
      • 第二轮: 问了一些微服务的八股(问的咋实现无状态？以及一些分布式基础理论对吧, 幂等idempotency, redis没问) 然后是写一个二叉搜索树, 能实现加节点和删除节点
      • 第三轮: 是lc31 和另一个给出每张图片需要处理的起始天和终点天[start, end],和每张图片处理一天需要的花费，n张图片，每天处理的总花费如果超过x，总花费就视为x，求处理所有图片的最少花费 不是lc原题 是hackerrank上的题目 第二题没写完 也过了
      • 最后一轮: 就是跟老板聊天 比较随意
    • Amazon:
      • bq: 亚麻bq大全, 答案要自己准备小故事, 16条军规 低职级的一般只考里面的10条, 4轮面试 每轮问两个不同的lp, 10选8, leadership principles, 就是军规, 其他公司的bq一般就是看你是不是个能一起工作的正常人, 亚麻是直接决定有没有offer
      • algo:
        • 都是原题, 亚麻coding很简单 主要是bq重要,
        • 店面问了一个trie
        • 两轮coding
          1. 一个是简单bfs(类似岛的数量number of islands, 经典中的经典了)
          2. 写一个能O1 add remove getrandom的set
    • okx:
      • 我还面了okx coinbase之后的炒币app第二名, payment组
      • algo: 一轮是lc49, 一轮是lc362
      • sd: sd是设计一个notification system
    • Google:
      • algo:
        • 除了google没人考dp, dp会几个经典的就行了(背包，股票，偷房子, 很多变形), dp难的是给竞赛生的,

概绍

本群的每日刷题打卡活动, 按照 GitHub 49k star的项目 https://github.com/youngyangyang04/leetcode-master 的刷题顺序.
跟着群里有个伴一起刷题或许更容易坚持达成每日一题的目标. 做完题目之后可以在群里的小程序”今日leetcode刷题打卡”里打卡.

  • 网页版: 代码随想录 https://programmercarl.com/
  • 本博客只记录那些有明显自我疑问而<<代码随想录>>没有说明清楚的题目, 会标识出来并注释

本文完整参考代码

https://github.com/no5ix/no5ix.github.io/blob/source/source/code/test_algo_na.java

Java常用接口和实现

Convert a number to a string and vice versa

1
2
3
4
5
6
int num = 123;
String str = String.valueOf(num);  // better
String str = num + ""; // worse, this method is simple but not efficient.

String str = "123";
int num = Integer.valueOf(str); // Returns an Integer object but can be unboxed to int

随机数

方法1: (推荐)

  • nextInt() 返回的是任意整数，范围包括负数和正数。
  • nextInt(bound) 返回一个随机整数，范围是从 0 到 bound（不包括 bound）。
1
2
3
4
5
6
7
8
9
10
// 如果你想生成一个 1 到 100 之间的随机整数（包括1和100），可以这样写：
Random random = new Random();
int randomNumber = random.nextInt(100) + 1; // 加1，使得范围变为 [1, 100]
System.out.println(randomNumber);

// Define the range [5, 10]
int min = 5;
int max = 10;
// Generate random number in the range [5, 10]
int randomNumber2 = random.nextInt((max - min) + 1) + min;

方法2: (不推荐)

To generate a random number within the range [3, 6], where both 3 and 6 are inclusive, you can modify the logic slightly from the [3, 6) approach: double randomNumber = 3 + (Math.random() * (6 - 3 + 1));

  1. Math.random() generates a random number in the range [0.0, 1.0).
  2. Multiplying it by (6 - 3 + 1) (which is 4) adjusts the range to [0.0, 4.0).
  3. Adding 3 shifts the range to [3.0, 7.0).
  4. Since the inclusive range is [3, 6], you’ll need to truncate or floor the result if you’re generating an integer: int picked = (int) ((high - low + 1) * Math.random()) + low;
  5. Notice: remember that int picked = (int) (high - low + 1) * Math.random() + low; is not correct, because it will cause the error “incompatible types: possible lossy conversion from double to int”, you should always convert the multiplication result ((high - low + 1) * Math.random()) to an Integer but not (high - low + 1) only

值传递

  • 记住：Java 中只有值传递！只是对于对象类型，值是对象的引用地址，这使得我们可以修改对象的内容，但不能改变对象的引用本身。
  • 基本数据类型： 方法接收变量的值，修改不会影响原始变量。
  • 对象类型：
    • 方法接收的是对象引用的副本，可以通过引用修改对象内容。
    • 方法不能改变引用本身的指向。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
//	解释：在 changeReference 方法中，person 被赋值为一个新的对象，但这只是改变了方法内的 person 引用，并不影响 main 方法中 p 的引用。
public class ReferenceReassignment {
    public static void main(String[] args) {
        Person p = new Person();
        p.name = "Alice";
        changeReference(p);
        System.out.println("Name after method call: " + p.name); // 输出 "Alice"
    }

    public static void changeReference(Person person) {
        person = new Person(); // 新建一个对象
        person.name = "Bob";  // 修改新对象的属性
    }
}

排序

普通递增排序:

1
2
3
4
5
6
7
// Arrays.sort 用于对数组进行排序（primitive 或 Object 类型）。
int[] nums = {3, 1, 4, 1, 5};
Arrays.sort(nums); // 对数组排序

// Collections.sort 用于对 List 集合进行排序（如 ArrayList、LinkedList 等）。
List<Integer> list = Arrays.asList(3, 1, 4, 1, 5);
Collections.sort(list); // 对 List 排序

举例说明自定义数字排序规则, 使用 Comparator:

  • Collections.sort
  • Arrays.sort

以下例子的这个排序逻辑首先按列 col 排序，如果列相同，则按行 row 排序，再根据节点的值进行排序。排序优先级依次是：列、行、值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// : List to store nodes with their column, row, and value
List<int[]> nodes = new ArrayList<>();
// nodes.add(new int[]{col, row, val});
nodes.add(new int[]{1, 2, 3});
nodes.add(new int[]{1, 3, 4});
nodes.add(new int[]{2, 2, 4});

// Sort nodes by column, row, and value
// 解释：
//     •	Collections.sort() 是 Java 中用于排序 List 的方法。它接受两个参数，第一个是需要排序的 List（在这里是 nodes），第二个是排序规则（通过 Comparator 来定义）。
//     •	这是一个 lambda 表达式，它实现了 Comparator<int[]> 接口。tuple1 和 tuple2 是 nodes 中的元素（即 int[] 类型的数组）。tuple1 和 tuple2 是用来比较的两个元素。
Collections.sort(nodes, (tuple1, tuple2) -> {
    // 排序规则:
    //     1.	首先比较 tuple1[0] 和 tuple2[0]：
    //          如果它们不相等（即列 col 不相同），则按列进行排序。
    //     2.	如果列相同，则比较 tuple1[1] 和 tuple2[1]：
    //          如果列相同，再按照行 row 进行排序。
    //     3.	如果列和行都相同，则比较 tuple1[2] 和 tuple2[2]：
    //          最后，如果列和行都相同，则按照节点的值进行排序。
    if (tuple1[0] != tuple2[0]) {
        // 这里的 tuple1[0] - tuple2[0] 是用来确定排序的方向。如果 tuple1[0] 小于 tuple2[0]，结果为负数，意味着 tuple1 排在 tuple2 前面；如果大于，结果为正数，tuple1 排在后面；如果相等，则继续比较后续条件。
        return tuple1[0] - tuple2[0];
    } else if (tuple1[1] != tuple2[1]) {
        return tuple1[1] - tuple2[1];
    } else {
        return tuple1[2] - tuple2[2];
    }
});

举例说明自定义字母排序规则 (比如有个 List 的list, 如何按照首字母的来排序): 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import java.util.*;

public class Main {
    public static void main(String[] args) {
        List<String> list = new ArrayList<>(Arrays.asList("apple", "banana", "cherry", "date", "grape"));

        // 按照首字母排序
        // • [推荐]	s1.charAt(0) 和 s2.charAt(0) 获取字符串的首字母。
        Collections.sort(list, (s1, s2) -> {  // 推荐这个方法
            return s1.charAt(0) - s2.charAt(0);
        });

        // • [不推荐]	Character.compare 是 Java 提供的方法，用于比较两个字符的大小。
        Collections.sort(list, (s1, s2) -> Character.compare(s1.charAt(0), s2.charAt(0))); // 不推荐, 因为Character.compare不好记

        System.out.println(list); // 输出: [apple, banana, cherry, date, grape]
    }
}

Map

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
Map<Integer, Integer> map = new HashMap<>();
map.put(1, 2);
map.put(2, 3);
map.get(1);
map.getOrDefault(1, 0);
map.containsKey(1);
map.size();
map.isEmpty();
// 如果你需要同时遍历键和值，通常会使用 Map.Entry 或 entrySet() 方法。
for (Map.Entry<Integer, Integer> es: map.entrySet()) {
    System.out.println(es.getKey());
    System.out.println(es.getValue());
}
// keySet(): 返回 Map 中所有键的 Set 视图。
for (int k : map.keySet()) {
    System.out.println(k);
}
// values(): 返回 Map 中所有值的 Collection 视图, 为啥不是valueSet, 因为value不是唯一的, 不是set
for (int v : map.values()) {
    System.out.println(v);
}
map.remove(1);
System.out.println(map);
map.clear();

Set

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Set<Integer> set = new HashSet<>();
set.add(2);
set.add(23);
set.add(231);
set.remove(231);
set.size();
set.isEmpty();
System.out.println("set.contains(2) : " + set.contains(2));
System.out.println("set.contains(231) : " + set.contains(231));
System.out.println(set);
set.clear();

// 从 Set<String> 转换为 String[]
Set<String> set = new HashSet<>(Arrays.asList("A", "B", "C"));
String[] array = set.toArray(new String[0]);
System.out.println(Arrays.toString(array));

List

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
List<Integer> list = new ArrayList<>();
list.add(11);
list.add(23);
list.add(31);
list.add(377);
list.size();
list.remove(0);  // 0 is index
list.get(0);
list.isEmpty();
for (int i : list) {
    System.out.println(i);
}
list.set(2, 33);
System.out.println("list: " + list);
list.clear();

//// 打印原生数组得
int[] ss = new int[2];
ss[0] = 2;
ss[1] = 1;

int[][] ssi = new int[2][2];
ssi[0][0] = 1;
ssi[0][1] = 2;

System.out.println(Arrays.toString(ss));  // 一维数组
System.out.println(Arrays.deepToString(ssi));  // 多维数组

//// slice operation
int[] points = {1, 2, 3, 4, 5};
int[] result = Arrays.copyOfRange(points, 0, 3); // result = {1, 2, 3}

List<Integer> list = Arrays.asList(1, 2, 3, 4, 5);
List<Integer> subList = list.subList(1, 4); // 切片：从索引 1 到 4（不包括 4）
System.out.println(subList); // 输出：[2, 3, 4]
    
///////////////////////
///  只要类实现了 Collection 接口，都支持 toArray() 方法。这包括：
//     •	List
//     •	Set
//     •	Queue
//     •	Deque
//     •	其他直接实现 Collection 的类
// 对于特定类型数组，推荐使用 toArray(T[] a) 方法，避免不必要的类型转换问题。
// List 转换为原生数组, 推荐使用这种方法，因为它直接返回指定类型的数组，避免类型转换问题。
List<String> list2 = Arrays.asList("A", "B", "C");
String[] array = list2.toArray(new String[0]); // 将集合中的元素存储到传入的数组`new String[0]`中，如果这个传入的数组容量不足(当前为0, 当然也可以写3就刚好够或者写2就不够, JVM 会自动分配合适大小的数组)，则会创建一个新数组。当然也可以直接传入合适的size (new String[list2.size()]);)
System.out.println(Arrays.toString(array));
String[] array2 = list2.toArray(new String[list2.size()]);  // 当然也可以直接传入合适的size

List<int[]> merged = new ArrayList<int[]>();
merged.toArray(new int[0][0]);

Queue

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Queue<Integer> queue = new ArrayDeque<>();  // 不要用 LinkedList(除非你要往队列里插入null, 因为ArrayDeque不准插入null, 但是LinkedList可以), ArrayDeque用circular buffer实现的, 是最高效的: https://stackoverflow.com/questions/6129805/what-is-the-fastest-java-collection-with-the-basic-functionality-of-a-queue
deque.offerFirst(1);
queue.offer(1);
queue.offer(2);
queue.isEmpty();
for (int i : queue) {
    System.out.println(i);
}
queue.poll();
System.out.println("queue: " + queue);
queue.peek();
queue.poll();
queue.size();
queue.clear();
queue.isEmpty();

Deque

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
Deque<Integer> deque = new ArrayDeque<>();  // 不要用 LinkedList(除非你要往队列里插入null, 因为ArrayDeque不准插入null, 但是LinkedList可以), ArrayDeque用circular buffer实现的, 是最高效的: https://stackoverflow.com/questions/6129805/what-is-the-fastest-java-collection-with-the-basic-functionality-of-a-queue
deque.offerFirst(1);
deque.offerLast(2);
deque.offerLast(23);
for (int i : deque) {
    System.out.println(i);
}
System.out.println(deque);
deque.pollFirst();
int resultValue = deque.pollLast();
int headValue = deque.peekFirst();
int tailValue = deque.peekLast();
System.out.println(resultValue);
System.out.println("deque: " + deque);
deque.clear();
deque.size();

Stack(一般不用因为有性能问题)

在 Java 中，如果我们希望避免使用 Stack 类以减少同步带来的性能问题，可以使用其他不包含同步的集合类实现栈（stack）的功能，例如 Deque（双端队列）。Deque 接口的实现类如 ArrayDeque 都是很好的选择。

1
2
3
4
5
6
7
Stack<Integer> stack = new Stack<>();
stack.push(1);
stack.peek();
stack.pop();
stack.isEmpty();
stack.size();
stack.clear();

String and Character

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
// Why use equals()?
// because == checks if the two objects are the same instance, whereas equals() compares the actual content of the strings.
String testStr = "aa";
if (testStr.equals("bb")) {
    System.out.println("testStr is equal to 'bb'");
}

// Character API
boolean realDigit = Character.isDigit('8');
boolean fakeDigit = Character.isDigit('u');
char testDigit = '9';
boolean res = Character.isLetterOrDigit(testDigit);
res = Character.toUpperCase(testDigit);
res = Character.toLowerCase(testDigit);

// String API
char[] charArr = {'a', 'b', 'c'};
String char2String = new String(charArr);

String str = " testString  ";
char[] charArray = str.toCharArray();
for (char c : str.toCharArray()) {
    System.out.println(c);
}
System.out.println(charArray);
System.out.println("str.length(): " + str.length());
str.charAt(2);
System.out.println("str.substring(1, 4) :" + str.substring(1, 4));  // output:tes, 因为substring不包含最后一个4索引的char
String trimedString = str.trim();
System.out.println("trimedString.substring(1, 4) :" + trimedString.substring(1, 4));  // output:est
str.isEmpty();
System.out.println(str);

// StringBuffer / StringBuilder API:
// StringBuffer / StringBuilder 的 append 方法被重载了，可以接受多种类型的参数，包括 int、long、float、double、char 等。注意事项：
// 	•	StringBuilder 是非线程安全的，但性能比 StringBuffer 更高，适用于单线程环境。
// 	•	如果需要线程安全的操作，应使用 StringBuffer。
StringBuilder sb = new StringBuilder("Hello");
// Append
sb.append(" World").append(123);
System.out.println(sb); // Hello World123
// Insert
sb.insert(5, ",");
System.out.println(sb); // Hello, World123
// Delete
sb.delete(5, 6);
System.out.println(sb); // Hello World123
// Replace
sb.replace(6, 11, "Java");
System.out.println(sb); // Hello Java123
// Reverse
sb.reverse();
System.out.println(sb); // 321avaJ olleH
String newStr = sb.toString();
System.out.println(newStr);

Quick Select

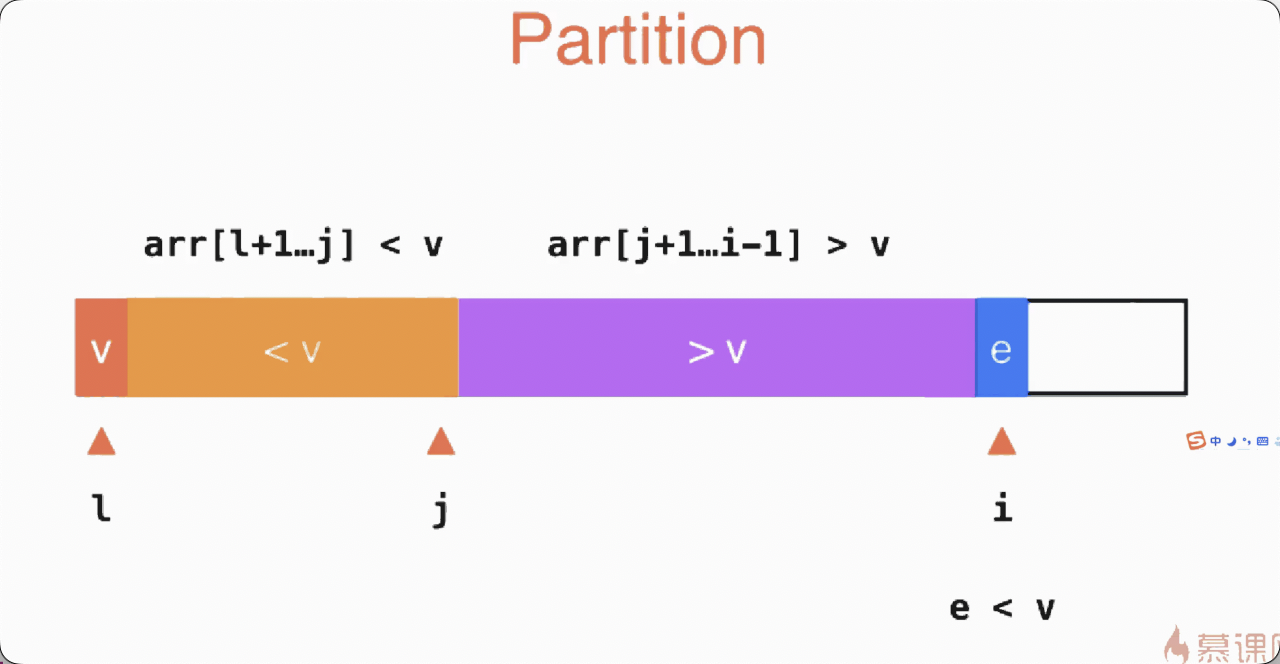
模板与诀窍

  • 适合解决 Top K 问题, 因为最快
  • 快速选择平均情况下，时间复杂度为 O(N)。
  • 空间复杂度：O(N)。哈希表的大小为 O(N)，用于排序的数组的大小也为 O(N)，快速排序的空间复杂度最好情况为 O(logN)，最坏情况为 O(N)。
  • 参考 algo_newbie.md ##普通快排 里的代码, 及其动画演示, 帮助理解
QuickSelect模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public int[] topK(int[] nums, int k) {
    int partitionIndex = 0;
    int targetIndex = nums.length - k;
    int left = 0;
    int right = pairLen - 1;
    while (true) {
        partitionIndex = quickSelect(nums, left, right);
        if (partitionIndex == targetIndex) {
            return res; 
        } else if (partitionIndex > targetIndex) {
            right = partitionIndex - 1;
        } else {
            left = partitionIndex + 1;
        }
    }
}

private int quickSelect(int[] nums, int left, int right) {
    int randIndex = (int) (Math.random() * (right - left + 1)) + left;
    swap(randIndex, left)

    Pair pivot = nums[left];
    int partitionIndex = left;  // 参考 algo_newbie.md ##普通快排 里的代码, 及其动画演示

    for (int i = left + 1; i <= right; ++i) {
        if (nums[i] < pivot) {
            swap(partitionIndex + 1, i)
            partitionIndex++;
        }
    }
    swap(left, partitionIndex);
    return partitionIndex;
}

lc347 - Top K Frequent Elements

We should solve this kind of top-level problem using the “Quick Select” approach (it’s very similar to Quick Sort). Because its time complexity of O(n) is lower, this method is more efficient than the Heap-based approach with a time complexity of O(nlogn).

Referenced this: https://www.bilibili.com/video/BV1Bz4y117Fr/

  • 时间复杂度：O(N)，其中 N 为数组的长度。
    设处理长度为 N 的数组的时间复杂度为 f(N)。由于处理的过程包括一次遍历和一次子分支的递归，最好情况下，有 f(N)=O(N)+f(N/2)，根据 主定理，能够得到 f(N)=O(N)。
  • 最坏情况下，每次取的中枢数组的元素都位于数组的两端，时间复杂度退化为 O(N)。但由于我们在每次递归的开始会先随机选取中枢元素，故出现最坏情况的概率很低。
  • 平均情况下，时间复杂度为 O(N)。
  • 空间复杂度：O(N)。哈希表的大小为 O(N)，用于排序的数组的大小也为 O(N)，快速排序的空间复杂度最好情况为 O(logN)，最坏情况为 O(N)。

链接：https://leetcode.cn/problems/top-k-frequent-elements/solutions/402568/qian-k-ge-gao-pin-yuan-su-by-leetcode-solution/

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
import java.util.Map;
import java.util.HashMap;

class Solution {

    public static void main(String[] args) {
        // int[] array = {10, 7, 8, 9, 1, 5};
        int[] array = {1, 1, 1, 1, 2, 2, 3, 3, 3, 5, 5, 5, 5, 6, 6};
        int[] res = topKFrequent(array, 2);
        // int[] array = {1};
        // int[] res = topKFrequent(array, 1);
        for (int num : res) {
            System.out.print("num: " + num + " ");
        }
    }
    
    public static int[] topKFrequent(int[] nums, int k) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        Pair[] pairs = new Pair[map.size()];
        int index = 0;
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) {
            pairs[index++] = new Pair(entry.getKey(), entry.getValue());
        }
        int partitionIndex = 0;
        int pairLen = pairs.length;
        int targetIndex = pairLen - k;
        int low = 0;
        int high = pairLen - 1;
        // System.out.println(high);
        while (true) {
            partitionIndex = quickSelect(pairs, low, high);
            if (partitionIndex == targetIndex) {
                int[] res = new int[k];
                for (int i = 0; i < k; ++i) {
                    res[i] = pairs[--pairLen].num;
                }
                return res; 
            } else if (partitionIndex > targetIndex) {
                high = partitionIndex - 1;
            } else {
                low = partitionIndex + 1;
            }
        }
    }

    private static int quickSelect(Pair[] pairs, int low, int high) {
        // System.out.println(low);
        // System.out.println(high);

        // To generate a random number within the range [3, 6], where both 3 and 6 are inclusive, you can modify the logic slightly from the [3, 6) approach:
        // double randomNumber = 3 + (Math.random() * (6 - 3 + 1));
        // 1.	Math.random() generates a random number in the range [0.0, 1.0).
        // 2.	Multiplying it by (6 - 3 + 1) (which is 4) adjusts the range to [0.0, 4.0).
        // 3.	Adding 3 shifts the range to [3.0, 7.0).
        // 4.	Since the inclusive range is [3, 6], you’ll need to truncate or floor the result if you’re generating an integer.

        int picked = (int) (Math.random() * (high - low + 1)) + low;
        Pair tempPair = pairs[low];
        pairs[low] = pairs[picked];
        pairs[picked] = tempPair;

        Pair pivot = pairs[low];
        int partitionIndex = low;  // 参考 algo_newbie.md ##普通快排 里的代码, 及其动画演示

        for (int i = low + 1; i <= high; ++i) {
            if (pairs[i].freq < pivot.freq) {
                Pair temp = pairs[i];
                pairs[i] = pairs[partitionIndex + 1];
                pairs[partitionIndex + 1] = temp;
                partitionIndex++;
            }
        }

        pairs[low] = pairs[partitionIndex];
        pairs[partitionIndex] = pivot;

        return partitionIndex;
    }

    static class Pair {
        int num;
        int freq;
        Pair(int number, int frequency) {
            num = number;
            freq = frequency;
        }
    }
}

数组

诀窍

没有思路的时候思考以下方法:

  • 口诀: “前二双排滑倒”
  • 先排个序
  • 前缀和(前缀和 在涉及计算区间和的问题时非常有用！)
  • 倒序遍历
  • 二分法(注意: int mid = left + (right - left) / 2;)
  • 双指针
  • 滑动窗口

二分法诀窍与易错点

  • 为什么要int mid = left + (right - left) / 2 ? 答案见下方代码中的注释
  • 是 while (leftIndex <= rightIndex) 还是 while (leftIndex < rightIndex) ? 答案见下方代码注释或者这里 的讲解
  • 二分查找, 当在数组中找不到对应的值, 循环完毕后的left和right的含义是什么?
    • 如果目标值不在数组中，循环结束时满足条件：right < left，循环结束后的 left 和 right 的含义如下:
    • left 的含义:
      • left 指向插入目标值的位置（满足排序要求）。
      • left 是第一个大于目标值的位置（在数组中的索引）。
      • 如果目标值比数组中所有元素都大，left 将等于数组的长度，即指向超出数组范围的位置。
    • right 的含义:
      • right 是目标值的前一个可能位置（如果目标值存在的话）。
      • right 是最后一个小于目标值的位置（在数组中的索引）。
      • 如果目标值比数组中所有元素都小，right 将等于 -1，即在数组范围之外。
    • 情况 1：目标值在数组范围内，但不存在
      • 数组为 [1, 3, 5, 7, 9]，目标值为 6。
        • • 最终状态：
        • • left = 3（第一个大于 6 的索引，值为 7）。
        • • right = 2（最后一个小于 6 的索引，值为 5）。
    • 情况 2：目标值比数组中所有元素小
      • 数组为 [3, 5, 7, 9]，目标值为 2。
        • • 最终状态：
        • • left = 0（第一个大于 2 的索引，值为 3）。
        • • right = -1（数组范围之外）。
    • 情况 3：目标值比数组中所有元素大
      • 数组为 [3, 5, 7, 9]，目标值为 10。
        • • 最终状态：
        • • left = 4（数组长度，超出范围）。
        • • right = 3（最后一个索引，值为 9）。
  • 比如说给你有序数组 nums = [1,2,2,2,3], target 为 2，如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3, 怎么做呢?
  • https://programmercarl.com/0704.二分查找.html#二分法第一种写法
  • https://leetcode.com/problems/binary-search/
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
class Solution {
    public int search(int[] numbers, int targetNumber) {
        if (targetNumber < numbers[0] || targetNumber > numbers[numbers.length - 1]) {
            return -1;
        }
        int leftIndex = 0;
        int rightIndex = numbers.length - 1;
        while (leftIndex <= rightIndex) {  // 因为我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right], 所以要使用 <= ，因为left == right是有意义的
            /*
            url: https://stackoverflow.com/questions/27167943/why-leftright-left-2-will-not-overflow
            Q: why left+(right-left)/2 can avoid overflow?
            A: 
                Suppose (to make the example easier) the maximum integer is 100, left = 50, and right = 80. If you use the naive formula:

                int mid = (left + right)/2;
                the addition will result in 130, which overflows.

                If you instead do:

                int mid = left + (right - left)/2;
                you can't overflow in (right - left) because you're subtracting a smaller number from a larger number. That always results in an even smaller number, so it can't possibly go over the maximum. E.g. 80 - 50 = 30.

                WWWWasp said: Since (right - left) is the distance between left and right, so `left + (right - left)/2` will not be larger than the right. Furthermore, it will not be larger than the maximum integer.
            */
            int midIndex = leftIndex + ((rightIndex - leftIndex) >> 1);  // >> 1 等同于 除以 2
            if (numbers[midIndex] == targetNumber) {
                return midIndex;
            } else if (numbers[midIndex] < targetNumber) {
                leftIndex = midIndex + 1;
            } else {
                rightIndex = midIndex - 1;
            }
        }
        return -1;
    }

    // 比如说给你有序数组 `nums = [1,2,2,2,3]`, target 为 2，但是如果我想得到 target 的左侧边界，即索引 1
    // 怎么做呢?
    int left_bound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] == target) {
                // 别返回，缩小右侧边界
                right = mid - 1;
            }
        }
        // 最后要检查 left 越界的情况
        if (left >= nums.length || nums[left] != target)
            return -1;
        return left;
    }

    // 比如说给你有序数组 `nums = [1,2,2,2,3]`, target 为 2，我想得到 target 的右侧边界，即索引 3, 
    // 怎么做呢?
    int right_bound(int[] nums, int target) {
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (nums[mid] < target) {
                left = mid + 1;
            } else if (nums[mid] > target) {
                right = mid - 1;
            } else if (nums[mid] == target) {
                // 别返回，缩小左侧边界
                left = mid + 1;
            }
        }
        // 最后要检查 right 越界的情况
        if (right < 0 || nums[right] != target)
            return -1;
        return right;
    }
}

二分查找扩展题-lc69-求平方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int mySqrt(int x) {
        if (x == 0 || x == 1) {
            return x;
        }
        int left = 1;
        int right = x;
        int mid = 0;
        while (left <= right) {
            mid = left + (right - left) / 2;
            if ((long)mid * mid > x) {
                right = mid - 1;
            } else if ((long)mid * mid < x) {
                left = mid + 1;
            } else {
                return mid;
            }
        }
        // 为什么返回right而不是left? 因为最后是left 大于了right才退出循环的, 所以要取小的那个, 退出循环的时候right小一些
        // 比如 x = 8, 此时 left=1, right=8, 则 [1, 2, 3, 4, 5, 6, 7, 8], 最后一轮循环是 left=3, right=3, 然后此时mid也等于3, 3*3=9 所以 right得减一, right 就等于2 了
        return right;
    }
}

前缀和诀窍

前缀和特别适合解决区间类的问题

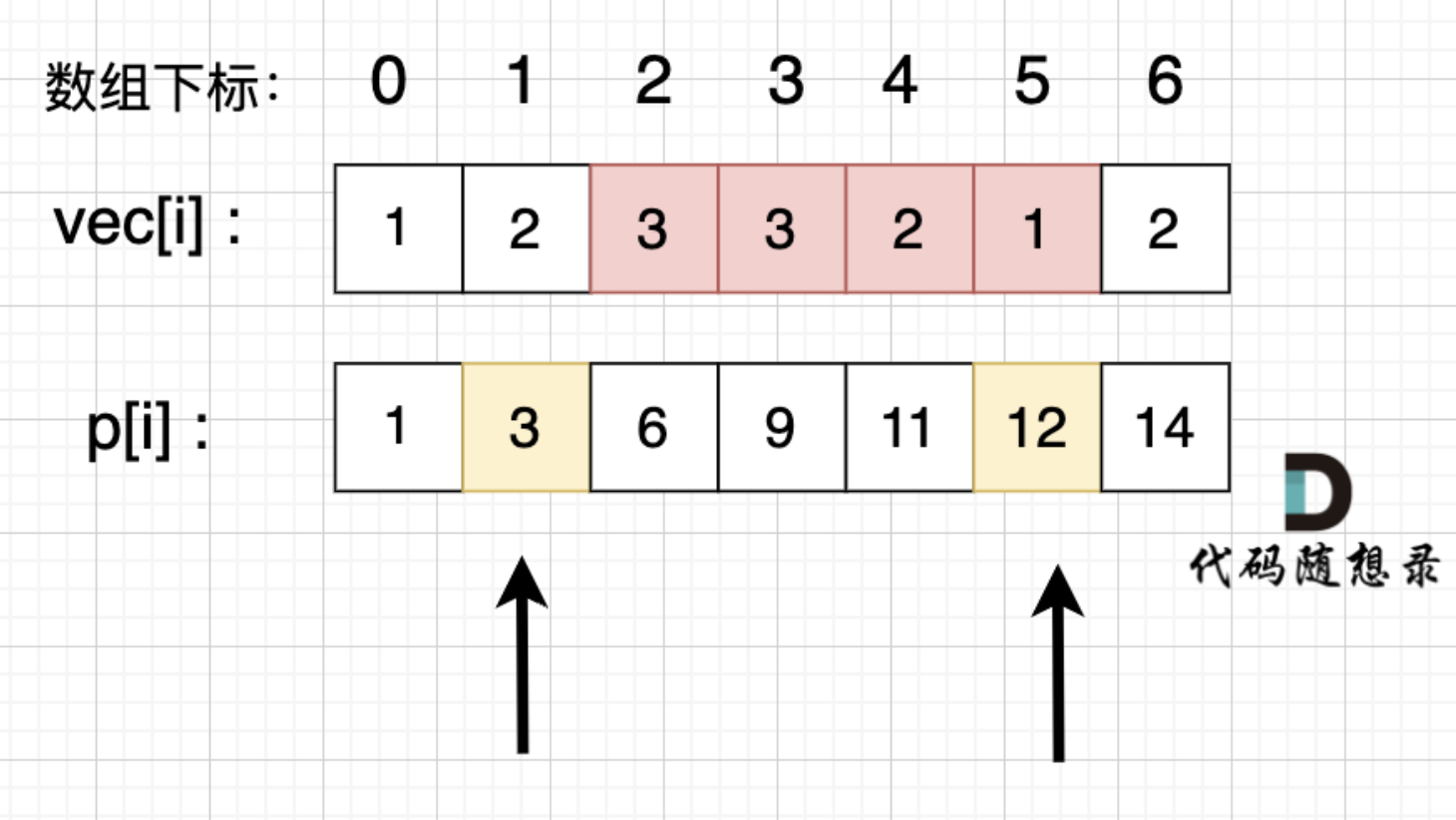
alt text

p[5] - p[1] 就是 红色部分的区间和。

而 p 数组是我们之前就计算好的累加和，所以后面每次求区间和的之后 我们只需要 O(1) 的操作。

特别注意： 在使用前缀和求解的时候，要特别注意 求解区间。

如上图，如果我们要求 区间下标 [2, 5] 的区间和，那么应该是 p[5] - p[1]，而不是 p[5] - p[2]。

「前缀和」 是从 nums 数组中的第 0 位置开始累加，到第 iii 位置的累加结果，我们常把这个结果保存到数组 preSum 中，记为 preSum[i]。

​
下面以 [1, 12, -5, -6, 50, 3] 为例，讲解一下如何求 preSum 前缀和的另一种写法(在很多题里非常有用, 比如这题):

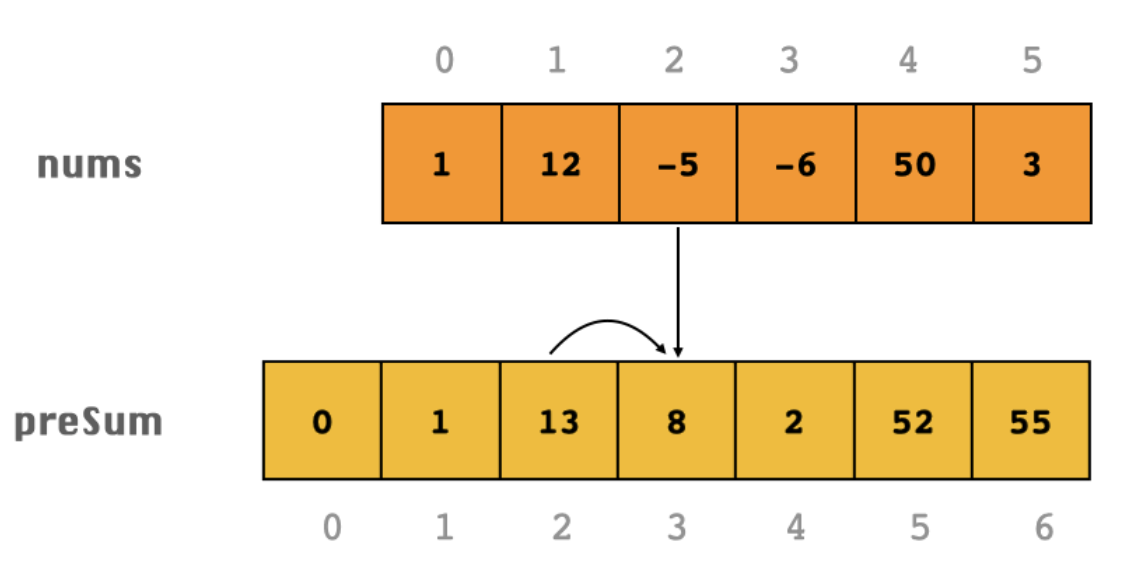
alt text

在前面计算「前缀和」的代码中，计算公式为 preSum[i] = preSum[i - 1] + nums[i] ，为了防止当 i = 0 的时候数组越界，所以加了个 if (i == 0) 的判断，即 i == 0 时让 preSum[i] = nums[i]。
​
在其他常见的写法中，为了省去这个 if 判断，我们常常把「前缀和」数组 preSum 的长度定义为 原数组的长度 + 1。preSum 的第 0 个位置，相当于一个占位符，置为 0。
那么就可以把 preSum 的公式统一为 preSum[i] = preSum[i - 1] + nums[i - 1]，此时的 preSum[i] 表示 nums 中 iii 元素左边所有元素之和（不包含当前元素 iii）。

1
2
3
4
5
6
7
for (int i = 1; i <= gain.length; i++) {
    prefixSum[i] = prefixSum[i - 1] + gain[i - 1];
}
// 或者
for (int i = 0; i < gain.length; i++) {
    prefixSum[i + 1] = prefixSum[i] + gain[i];
}

lc528-前缀和+二分

lc528 Description:

You are given a 0-indexed array of positive integers w where w[i] describes the weight of the ith index.

You need to implement the function pickIndex(), which randomly picks an index in the range [0, w.length - 1] (inclusive) and returns it. The probability of picking an index i is w[i] / sum(w).

For example, if w = [1, 3], the probability of picking index 0 is 1 / (1 + 3) = 0.25 (i.e., 25%), and the probability of picking index 1 is 3 / (1 + 3) = 0.75 (i.e., 75%).

Example 1:

  • Input
    • ["Solution","pickIndex"]
    • [[[1]],[]]
  • Output : [null,0]
  • Explanation:
    Solution solution = new Solution([1]);
    solution.pickIndex(); // return 0. The only option is to return 0 since there is only one element in w.

Example 2:

  • Input:
    • ["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"]
    • [[[1,3]],[],[],[],[],[]]
  • Output: [null,1,1,1,1,0]

  • Explanation:
    Solution solution = new Solution([1, 3]);
    solution.pickIndex(); // return 1. It is returning the second element (index = 1) that has a probability of 3/4.
    solution.pickIndex(); // return 1
    solution.pickIndex(); // return 1
    solution.pickIndex(); // return 1
    solution.pickIndex(); // return 0. It is returning the first element (index = 0) that has a probability of 1/4.

    Since this is a randomization problem, multiple answers are allowed.
    All of the following outputs can be considered correct:
    [null,1,1,1,1,0]
    [null,1,1,1,1,1]
    [null,1,1,1,0,0]
    [null,1,1,1,0,1]
    [null,1,0,1,0,0]
    ……
    and so on.

Constraints:

  • 1 <= w.length <= 104
  • 1 <= w[i] <= 105
  • pickIndex will be called at most 104 times.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
class Solution {
    int[] wSum;
    Random random = new Random();

    public Solution(int[] w) {
        for (int i = 1; i < w.length; ++i) {
            w[i] += w[i - 1];
        }
        this.wSum = w;
    }
    
    public int pickIndex() {
        return this.binarySearch();
    }

    private int binarySearch() {
        int left = 0;
        int right = this.wSum.length - 1;
        int randNum = random.nextInt(this.wSum[this.wSum.length - 1]) + 1; 
        while (left <= right) {
            int mid = left + (right - left) / 2;
            if (wSum[mid] == randNum) {
                return mid;
            } else if (wSum[mid] < randNum) {
                left = mid + 1;
            } else if (wSum[mid] > randNum) {
                right = mid - 1;
            }
        }
        // Why return left??  @see ## 二分法诀窍与易错点
        // Example Walkthrough
        // Input: w = [1, 3, 6]
        // Cumulative weights (wSum): [1, 4, 10]
        // Suppose randNum = 5.
        //     1.	Initial pointers: left = 0, right = 2.
        //     2.	First iteration:
        //     •	mid = 1 ((0 + 2) / 2).
        //     •	wSum[mid] = 4, which is less than randNum.
        //     •	Adjust left to mid + 1 → left = 2.
        //     3.	Second iteration:
        //     •	mid = 2.
        //     •	wSum[mid] = 10, which is greater than randNum.
        //     •	Adjust right to mid - 1 → right = 1.
        //     4.	Exit loop: left = 2, right = 1.
        // Result:
        //     •	left = 2, which is the correct index (wSum[2] = 10 covers randNum = 5).
        //     •	right = 1 would be incorrect because randNum is not in the range of wSum[1].
        return left;
    }
}

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(w);
 * int param_1 = obj.pickIndex();
 */

双指针诀窍

双指针和滑动窗口的一般不同点是:

  • 双指针大多数时候是left指针在首, right在尾, 然后互相逐渐靠近
  • 或者一个快一个慢, right快(去寻找合适的数), left慢的指针就处理right找到数据; 而滑动窗口一般也是right快left慢但是为了维护一个区间窗口, 一般是用来求一个区间的最大最小和之类的东西
  • 理论上滑动窗口是双指针的一种, 只是比较像一个窗口而故名

lc27-Remove Element

双指针法（快慢指针法）： 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针:

  • 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
  • 慢指针：指向更新 新数组下标的位置

诀窍: 应该想象成 slowIndex 之前的那些数组格子就是新的数组

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
    public int removeElement(int[] nums, int val) {
        int slowIndex = 0;
        int fastIndex = 0;
        for (;fastIndex < nums.length; fastIndex++) {
            if (nums[fastIndex] != val) {
                nums[slowIndex++] = nums[fastIndex];
            }
        }
        return slowIndex;
    }
}

lc977-有序数组的平方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {  // lc977
    public int[] sortedSquares(int[] nums) {
        int[] resultArray = new int[nums.length];
        int startIndex = 0;
        int endIndex = nums.length - 1;
        int resultIndex = nums.length - 1;
        while (startIndex <= endIndex) {  // 这里是 <= , 因为最后相等时候的那个元素也要处理
            if (nums[startIndex] * nums[startIndex] > nums[endIndex] * nums[endIndex]) {
                resultArray[resultIndex--] = nums[startIndex] * nums[startIndex];
                startIndex++;
            } else {
                resultArray[resultIndex--] = nums[endIndex] * nums[endIndex];
                endIndex--;
            }
        }
        return resultArray;
    }
}

public class test{
    public static void main(String[] args){
        Solution solution = new Solution();
        int[] myList = {-7, 2, 3, 5, 6};
        int[] ret = solution.sortedSquares(myList);
        System.out.println(ret);
        for (int i = 0; i < ret.length; ++i) {
            System.out.println(ret[i]);
        }
    }
}

lc15-3Sum

其实这道题目使用哈希法并不十分合适(4sum就没办法了)，因为在去重的操作中有很多细节需要注意，在面试中很难直接写出没有bug的代码。
接下来我来介绍另一个解法：双指针法(4sum也是这种思路)，这道题目使用双指针法 要比哈希法高效一些，那么来讲解一下具体实现的思路。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        Arrays.sort(nums);
	    // 找出a + b + c = 0
        // a = nums[i], b = nums[left], c = nums[right]
        for (int i = 0; i < nums.length; i++) {
	    // 排序之后如果第一个元素已经大于零，那么无论如何组合都不可能凑成三元组，直接返回结果就可以了
            if (nums[i] > 0) { 
                // return result;  用 return不好, 用break好些, 和4sum用break统一了
                break;
            }

            if (i > 0 && nums[i] == nums[i - 1]) {  // 去重a
                continue;
            }

            int left = i + 1;
            int right = nums.length - 1;
            while (right > left) {
                int sum = nums[i] + nums[left] + nums[right];
                if (sum > 0) {
                    right--;
                } else if (sum < 0) {
                    left++;
                } else {
                    result.add(Arrays.asList(nums[i], nums[left], nums[right]));
		    // 去重逻辑应该放在找到一个三元组之后，对b 和 c去重
                    while (right > left && nums[right] == nums[right - 1]) right--;
                    while (right > left && nums[left] == nums[left + 1]) left++;
                    
                    right--; 
                    left++;
                }
            }
        }
        return result;
    }
}

lc18-4Sum

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
    public static List<List<Integer>> fourSum(int[] nums, int target) {
        Arrays.sort(nums);
        List<List<Integer>> resultList = new ArrayList<>();

        for (int i = 0; i < nums.length; ++i) {
            if (nums[i] >= 0 && nums[i] > target) {
                break;
            }
            if (i > 0 && nums[i] == nums[i - 1]) {
                continue;
            }
            for (int j = i + 1; j < nums.length; ++j) {
                if (nums[i] + nums[j] >= 0 && nums[i] + nums[j] > target) {
                    System.out.println("i:" + i + ", j:" + j);
                    // return resultList; // return resultList;  // can't return here, considering [-3,-2,-1,0,0,1,2,3] , i = 1, j = 7, would lose [-1, 0, 0, 1]
                    break;
                }
                if (j > i + 1 && nums[j] == nums[j - 1]) {
                    continue;
                }
                int left = j + 1;
                int right = nums.length - 1;
                while (left < right) {
                    long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
                    if (sum > target) {
                        right--;
                    } else if (sum < target) {
                        left++;
                    } else {
                        resultList.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
                        while (left < right && nums[left + 1] == nums[left]) {
                            left++;
                        }
                        while (left < right && nums[right - 1] == nums[right]) {
                            right--;
                        }
                        right--;
                        left++;
                    }
                }
            }
        }
        return resultList;
    }

    public static void main(String[] args) {
        // int[] testArr = {2, 2, 2, 2, 2};
        int[] testArr = {-3,-2,-1,0,0,1,2,3};
        // int[] testArr = {2, 3, 1, 2, 2};
        // int target = 8;
        // int[] testArr = {1,0,-1,0,-2,2};
        int target = 0;
        List<List<Integer>> result = fourSum(testArr, target);
        for (List<Integer> arr : result) {
            System.out.println(arr);
        }
    }
}

滑动窗口模板与生动理论

  • https://leetcode.cn/problems/max-consecutive-ones-iii/solutions/609055/fen-xiang-hua-dong-chuang-kou-mo-ban-mia-f76z/
  • 《挑战程序设计竞赛》这本书中把滑动窗口叫做「虫取法」，我觉得非常生动形象。因为滑动窗口的两个指针移动的过程和虫子爬动的过程非常像：前脚不动，把后脚移动过来；后脚不动，把前脚向前移动。
  • 滑动窗口中用到了左右两个指针，它们移动的思路是：以右指针作为驱动，拖着左指针向前走。右指针每次只移动一步，而左指针在内部 while 循环中每次可能移动多步。右指针是主动前移，探索未知的新区域；左指针是被迫移动，负责寻找满足题意的区间。

滑动窗口的模板，能解决大多数的滑动窗口问题：

滑动窗口的模板
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def findSubArray(nums):
    N = len(nums) # 数组/字符串长度
    left, right = 0, 0 # 双指针，表示当前遍历的区间[left, right]，闭区间
    sums = 0 # 用于统计 子数组/子区间 是否有效，根据题目可能会改成求和/计数
    res = 0 # 保存最大的满足题目要求的 子数组/子串 长度
    while right < N: # 当右边的指针没有搜索到 数组/字符串 的结尾
        sums += nums[right] # 增加当前右边指针的数字/字符的求和/计数
        while 区间[left, right]不符合题意: # 此时需要一直移动左指针，直至找到一个符合题意的区间
            sums -= nums[left] # 移动左指针前需要从counter中减少left位置字符的求和/计数
            left += 1 # 真正的移动左指针，注意不能跟上面一行代码写反
        # 到 while 结束时，我们找到了一个符合题意要求的 子数组/子串
        res = max(res, right - left + 1) # 需要更新结果
        right += 1 # 移动右指针，去探索新的区间
    return res

lc1004-Max Consecutive Ones III

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int longestOnes(int[] A, int K) {
        int left = 0;
        int right = 0;
        int zeroCount = 0;
        int result = 0;
        while (right < A.length) {
            if (A[right] == 0) {
                zeroCount++;
            }
            while (zeroCount > K) {
                if (A[left] == 0) {
                    zeroCount--;
                }
                left++;
            }
            result = Math.max(result, right - left + 1);
            right++;
        }
        return result;
    }
}

链表

诀窍

  • 没有思路的时候想想快慢指针, 能解决大部分链表问题
  • 单链表弄个虚拟头结点, 可以很省事
  • 双链表弄个虚拟头结点和虚拟尾结点, 刚开始就让虚拟头尾相连, 可以很省事, 参见LRU里的那个, 如下: 
    1
    2
    3
    4
    this.head = new DLinkedNode();  // dummy
    this.tail = new DLinkedNode();  // dummy
    head.next = tail;
    tail.pre = head;  // 刚开始初始化的时候虚拟首尾节点的中间没有实际节点, 所以虚拟首尾节点是相连的.

lc206 - 链表反转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 双指针
class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode cur = head;
        ListNode prev = null;
        ListNode temp = null;
        while (cur != null) {
            temp = cur.next;// 保存下一个节点
            cur.next = prev;
            prev = cur;
            cur = temp;
        }
        return prev;
    }
}

lc24 - 两两交换链表中的节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 将步骤 2,3 交换顺序，这样不用定义 temp 节点
public ListNode swapPairs(ListNode head) {
    ListNode dummy = new ListNode(0, head);
    ListNode cur = dummy;
    while (cur.next != null && cur.next.next != null) {
        ListNode node1 = cur.next;// 第 1 个节点
        ListNode node2 = cur.next.next;// 第 2 个节点
        cur.next = node2; // 步骤 1
        node1.next = node2.next;// 步骤 3
        node2.next = node1;// 步骤 2
        cur = cur.next.next;
    }
    return dummy.next;
}

字符串

lc28 - 实现strStr() - 20240923

暴力解法-掌握这个暴力解法即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int strStr(String haystack, String needle) {
        int hLen = haystack.length();
        int nLen = needle.length();
        // 0, 1, 2, 3, 4, 5
        for (int i = 0; i + nLen <= hLen; ++i) {
            boolean flag = true;
            for (int j = 0; j < nLen; ++j) {
                if (haystack.charAt(i + j) != needle.charAt(j)) {
                    flag = false;
                    break;
                }
            }
            if (flag == true) {
                return i;
            }
        }
        return -1;
    }
}

KMP不要求-面试基本不会出的-背代码就没意思了

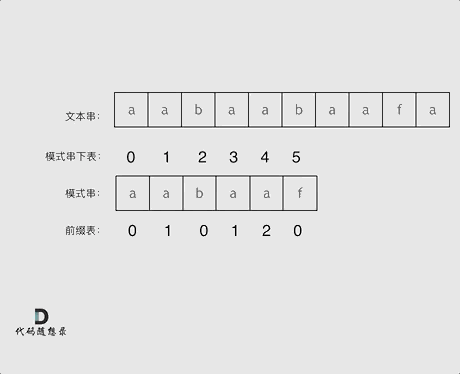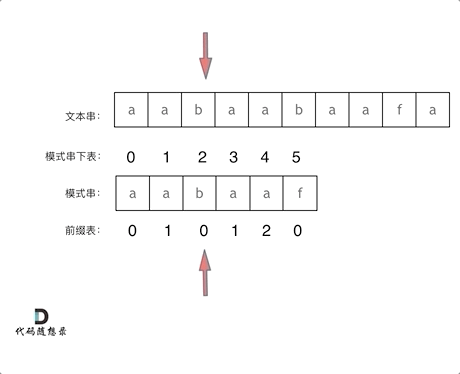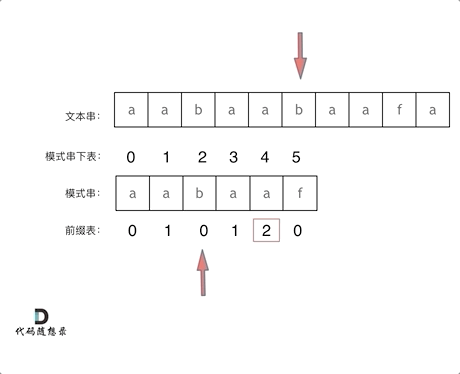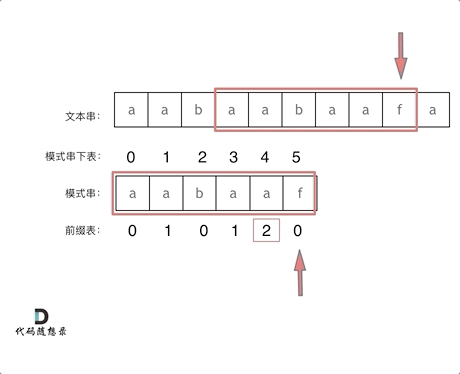
看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如上动画所示：

找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。

为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀。

所以要看前一位的 前缀表的数值。

前一个字符的前缀表的数值是2， 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。

最后就在文本串中找到了和模式串匹配的子串了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    //前缀表（不减一）Java实现
    public int strStr(String haystack, String needle) {
        if (needle.length() == 0) return 0;
        int[] next = new int[needle.length()];  // 前缀表
        getNext(next, needle);

        int j = 0;  // 此处 j 指向 基于模式串 needle 的 内部的起始位置
        for (int i = 0; i < haystack.length(); i++) {  // i 指向 基于文本串 haystack 内部的起始位置。
            while (j > 0 && needle.charAt(j) != haystack.charAt(i)) 
                j = next[j - 1];  // strStr 里匹配过程里的寻找前一位来继续匹配; 不懂的话看视频 https://www.bilibili.com/video/BV1PD4y1o7nd/?vd_source=8a83b38420b65ac33aa101b7754630f6 里的 "使用前缀表的匹配过程" 环节
            if (needle.charAt(j) == haystack.charAt(i)) 
                j++;
            if (j == needle.length())  // 当 j 等于needle 长度的时候, 说明 j 指向了模式串t的末尾的后面，那么就说明模式串t完全匹配文本串s里的某个子串了。
                return i - needle.length() + 1;
        }
        return -1;

    }
    
    private void getNext(int[] next, String s) {
        int j = 0;  // 此处 j 是 前缀 的末尾位置, 也是前缀的长度
        next[0] = 0;
        for (int i = 1; i < s.length(); i++) {  // i 是后缀的末尾位置
            while (j > 0 && s.charAt(j) != s.charAt(i))  // 此时前后缀不相等; (j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1];  // 注意这里，是要找前一位的对应的回退位置了; 为什么这里要找前一位的对应的回退位置呢? 因为和 上面 strStr 里匹配过程里的寻找前一位来继续匹配是一样一样的
            if (s.charAt(j) == s.charAt(i))   // 此时前后缀相等
                j++;
            next[i] = j;  // 因为 j 既是前缀 的末尾位置, 又是前缀的长度, 所以此处直接在 next 表里存下 j
        }
    }
}

lc459 - 重复的子字符串-暴力解法-掌握这个暴力解法即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
// 作者：力扣官方题解
// 链接：https://leetcode.cn/problems/repeated-substring-pattern/solutions/386481/zhong-fu-de-zi-zi-fu-chuan-by-leetcode-solution/
class Solution {
    public boolean repeatedSubstringPattern(String s) {
        int n = s.length();
        for (int i = 1; i * 2 <= n; ++i) {  // 这个 i 并不是 字符串的index, 而是子串长度; 并且注意到一个小优化是，因为子串至少需要重复一次，所以子串长度 i 不会大于 n 的一半，
            if (n % i == 0) {  // s 的长度一定是子串长度的倍数
                boolean match = true;
                for (int j = i; j < n; ++j) {
                    int offset = j % i;  // 子串肯定是 s 的前缀, 这里是拿字符串的子串前缀的index
                    if (s.charAt(j) != s.charAt(offset)) {
                        match = false;
                        break;
                    }
                }
                if (match) {
                    return true;
                }
            }
        }
        return false;
    }
}

栈与队列

诀窍

  • 当遇到这类问题就要用栈了:
    • 栈在系统中的路径问题, 如: 简化路径 cd a/b/c/../../
    • 括号匹配问题, 如: 给定一个只包括'('，')'，'{'，'}'，'['，']'的字符串，判断字符串是否有效。
    • 字符串去重问题, 如: lc1047. 删除字符串中的所有相邻重复项
  • 队列反而是在树的层序遍历里用的较多

lc239 - Sliding Window Maximum

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//利用双端队列手动实现单调队列
/**
 * 用一个单调队列来存储对应的下标，每当窗口滑动的时候，直接取队列的头部指针对应的值放入结果集即可
 * 单调队列类似 （tail -->） 3 --> 2 --> 1 --> 0 (--> head) (右边为头结点，元素存的是下标)
 */
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        Deque<Integer> deque = new ArrayDeque<>();
        int n = nums.length;
        int[] res = new int[n - k + 1];
        int j = 0;
        for (int i = 0; i < n; ++i) {
            // 根据题意，i为nums下标，是要在[i - k + 1, i] 中选到最大值，只需要保证两点
            // 1.队列头结点需要在[i - k + 1, i]范围内，不符合则要弹出
            while (!deque.isEmpty() && deque.peekFirst() < i - k + 1) {
                deque.pollFirst();
            }
            // 2.既然是单调，就要保证每次放进去的数字要比末尾的都大，否则也弹出
            while (!deque.isEmpty() && nums[i] > nums[deque.peekLast()]) {
                deque.pollLast();
            }
            deque.addLast(i);

            // 因为单调，当i增长到符合第一个k范围的时候，每滑动一步都将队列头节点放入结果就行了
            if (i >= k - 1 ) {
                res[j++] = nums[deque.peekFirst()];
            }
        }
        return res;
    }
}

二叉树

诀窍

  • 一共只有三种题目:
    • 直接通过 dfs/bfs 可以计算的类型
    • 路径类
    • 最小祖先类
  • 二叉树最重要的是层序遍历的模板, 可以解决 70% 的二叉树题目
  • 路径题和公共祖先题和深度高度的题一般才会用到 递归, 其他大多数时候都可以层序遍历 / 前中序遍历的迭代法解决
  • 二叉树递归写法诀窍, 递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

层序(相当重要)

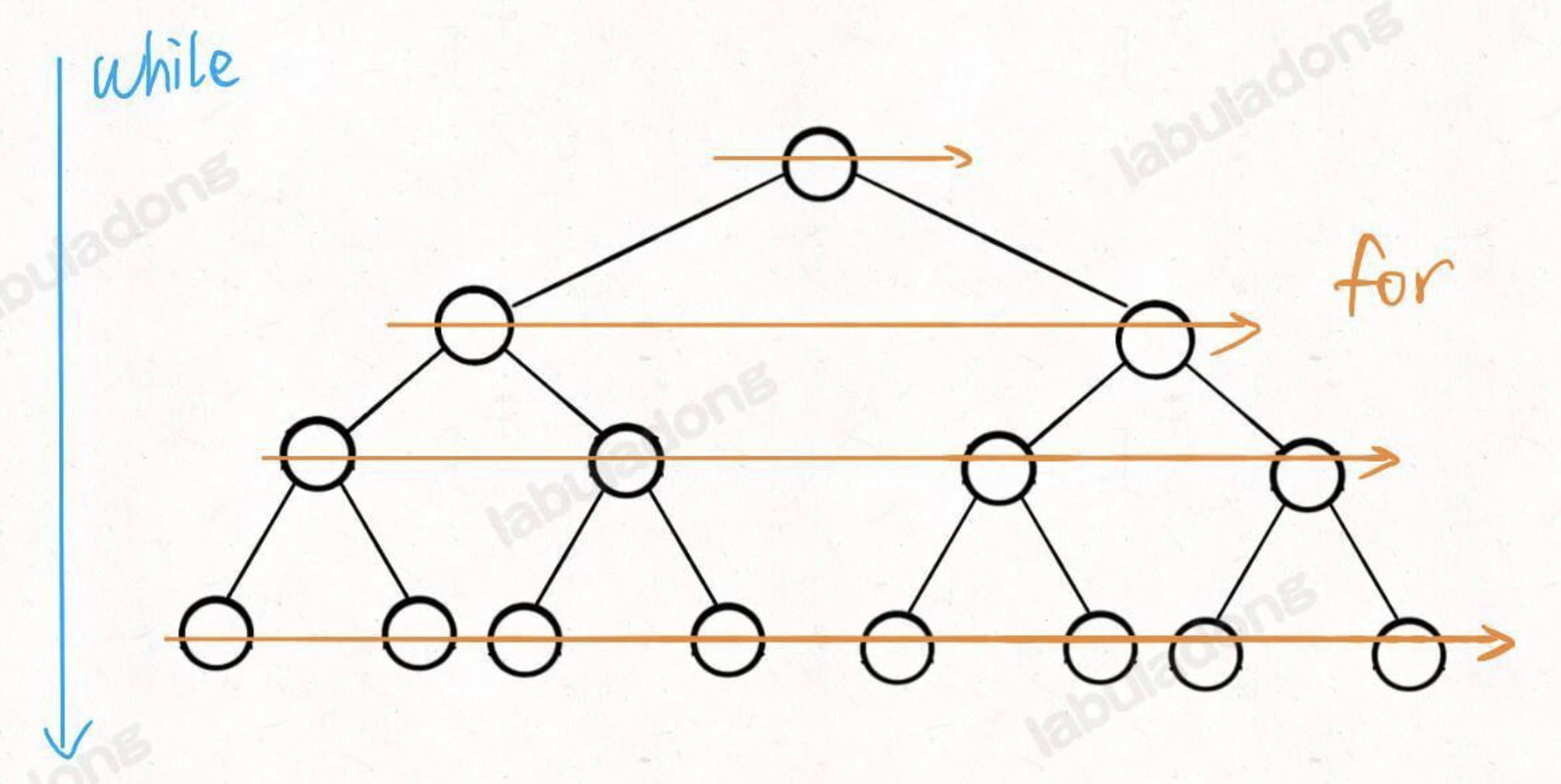
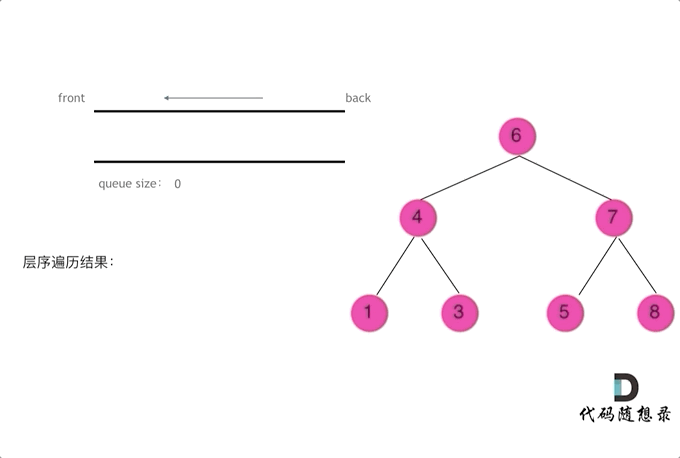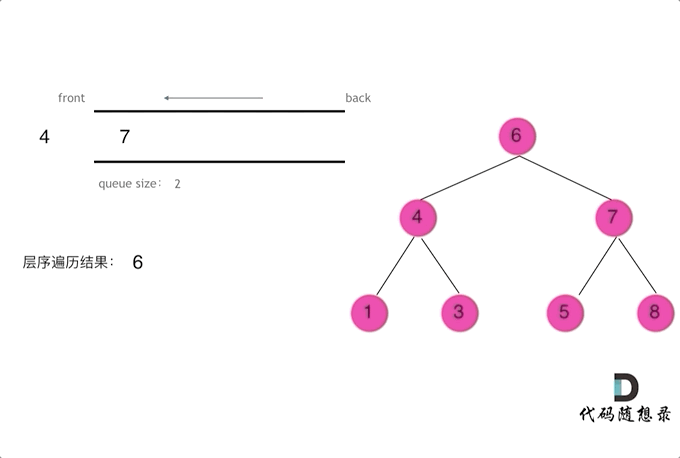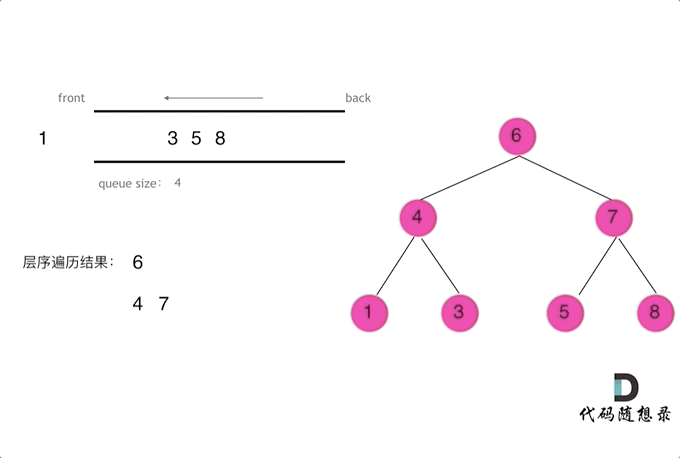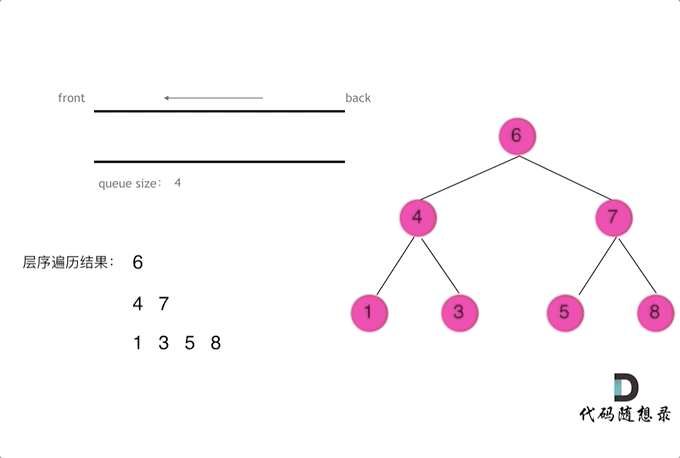
  • 注意 while (len > 0) { } 这个代码块里的就是同一层的结点处理
  • 掌握了这个模板, 可以解决 70% 的二叉树题目
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    // // 注意返回值是List<List<Integer>>不是单List<Integer>, 因为层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树, 每一层都是一个 List<Integer>, 所以每一层加起来组成一个大的 List<List<Integer>>
    public List<List<Integer>> levelOrder(TreeNode root) {  
        List<List<Integer>> resultList = new ArrayList<List<Integer>>();
        if (root == null ) {
            return resultList;
        }
        Queue<TreeNode> que = new LinkedList<TreeNode>();
        que.offer(root);  // 循环外就第一次 push了root
        int depth = 0;  // 深度, 非常实用
        while (!que.isEmpty()) {
            List<Integer> itemList = new ArrayList<Integer>();
            int len = que.size();  // 注意这个len, 这里一定要使用固定大小 len，不要使用que.size()，因为que.size是不断变化的
            depth++;
            while (len > 0) {  // 这个代码块里的就是同一层的结点处理
                TreeNode tmpNode = que.poll();
                itemList.add(tmpNode.val);

                if (tmpNode.left != null) { que.offer(tmpNode.left); }
                if (tmpNode.right != null) { que.offer(tmpNode.right); }
                len--;
            }
            resultList.add(itemList);
        }

        return resultList;
    }
}

前序(迭代法重要)

  • 普通二叉树常用
  • 前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。
  • 为什么要先加入 右孩子，再加入左孩子呢？ 因为这样出栈的时候才是中左右的顺序。
  • 掌握了之后可以求 路径 问题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) { return result; }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);  // 和中序不同: 循环外就第一次 push了root
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(node.val);
            // 为什么要先加入 右孩子，再加入左孩子呢？ 因为这样出栈的时候才是中左右的顺序。
            if (node.right != null) { stack.push(node.right); }
            if (node.left != null) { stack.push(node.left); }
        }
        return result;
    }
}

中序(迭代法重要)

  • 二叉搜索树BST常用, 因为 BST 的 中序遍历 出来是个有序的递增数组)
  • 中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。
  • 那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {  // 和前序迭代法不同: 这里多判断了cur不等于null
            if (cur != null) {
                stack.push(cur);  // 和前序迭代法不同: 循环内才第一次 push了root
                cur = cur.left;  // 左
            } else {
                cur = stack.pop();
                result.add(cur.val);  // 中
                cur = cur.right;  // 右
            }
        }
        return result;
    }
}

后序(迭代法不重要)

  • 后序迭代法很少用到, 会前序按照以下方法就会写后序:
    1. 先序遍历是中左右
    2. 调整代码左右循序
    3. 变成中右左 -> 反转result数组 -> 左右中
    4. 后序遍历是左右中
  • 后序遍历的递归法用得着, 那种需要从树底下往上走来统计信息的就用得到, 如 公共祖先 这种题就需要后序遍历递归法

路径(重要)

https://leetcode.com/problems/path-sum-ii/description/

Given the root of a binary tree and an integer targetSum, return all root-to-leaf paths where the sum of the node values in the path equals targetSum. Each path should be returned as a list of the node values, not node references.

A root-to-leaf path is a path starting from the root and ending at any leaf node. A leaf is a node with no children.

  • 要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。
  • 注意其中的回溯, 特别是 count 的回溯注释, 方便深刻的理解回溯
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    List<List<Integer>> result;
    LinkedList<Integer> path;

    public List<List<Integer>> pathSum (TreeNode root,int targetSum) {
        result = new LinkedList<>();
        path = new LinkedList<>();
        travesal(root, targetSum);
        return result;
    }

    private void travesal(TreeNode root,  int count) { // 这个版本最好, 最容易想得到, 符合直觉
        if (root == null) return;
        path.offer(root.val);
        count -= root.val;
        if (root.left == null && root.right == null && count == 0) {
            result.add(new LinkedList<>(path));
        }
        travesal(root.left, count);
        travesal(root.right, count);
        path.removeLast(); // 回溯
        count += root.val;  // 按道理说, 这一行不能注释, 这里返回上一层递归是应该要回溯的, 但是因为 count 只是个int, 不是全局变量, 不会影响上一层的 count, 所以这一行其实可以注释
    }
}

高度

  • 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数
  • 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数
  • 根节点的高度就是二叉树的最大深度

深度

  • 求深度用层序遍历是最适合的最直观容易理解
  • 二叉树的深度: 根节点到最远叶子节点的最长路径上的节点数。
  • 叶子节点: 是指没有子节点的节点。

最大深度

使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。
在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，

迭代法

层序遍历:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int depth = 0;
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        while (!que.isEmpty()) {
            int len = que.size();
            depth++;
            while (len > 0) {
                TreeNode tmpNode = que.poll();
                if (tmpNode.left != null) { que.offer(tmpNode.left); }
                if (tmpNode.right != null) { que.offer(tmpNode.right); }
                len--;
            }
        }
        return depth;
    }
}

递归法1-回溯(重要)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    
    int maxNum = 0; // 定义最大深度 

    public int maxDepth(TreeNode root) {
        ans(root, 0);
        return maxNum;
    }
    
    // 递归解法1: 
    void ans(TreeNode tr, int depth){
        if(tr == null) return;
        // 递归开始，深度增加
        depth++;
        maxNum = maxNum < depth ? depth : maxNum;
        ans(tr.left, depth);
        ans(tr.right, depth);
        // 递归结束, 得回溯，深度减少
        depth--;
    }
    
    //递归解法2: 
    void ans(TreeNode tr, int depth){
        if(tr == null) return;
        maxNum = maxNum < depth + 1 ? depth + 1 : maxNum;
        ans(tr.left, depth + 1);  // 隐含了回溯, 因为depth实际上自身没有变, 这里并不是
        ans(tr.right, depth + 1);
    }
}

递归法2

后序遍历, 掌握后可以解 树的最大直径 lc543: https://leetcode.com/problems/diameter-of-binary-tree/description/):

1
2
3
4
5
6
7
8
9
10
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0; // 访问到空节点了，返回0
        }
        int leftDepth = maxDepth(root.left);
        int rightDepth = maxDepth(root.right);
        return Math.max(leftDepth, rightDepth) + 1;  // 这个 +1 的 1 是指当前层自己本身这个结点
    }
}

最小深度

最小深度: 是从根节点到最近叶子节点的最短路径上的节点数量。

迭代法

层序遍历:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int depth = 0;
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        while (!que.isEmpty()) {
            int len = que.size();
            depth++;
            while (len > 0) {
                TreeNode tmpNode = que.poll();
                if (tmpNode.left == null && tmpNode.right == null) {
                    // 当左右孩子都为空的时候，说明是最低点的一层了，退出
                    return depth;
                }
                if (tmpNode.left != null) { que.offer(tmpNode.left); }
                if (tmpNode.right != null) { que.offer(tmpNode.right); }
                len--;
            }
        }
        return depth;
    }
}

递归法-回溯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
    /**
     * 递归法（思路来自二叉树最大深度的递归法）
     * 该题求最小深度，最小深度为根节点到叶子节点的深度，所以在迭代到每个叶子节点时更新最小值。
     */
    int depth = 0;
    // 定义最小深度，初始化最大值
    int minDepth = Integer.MAX_VALUE;

    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        dep(root);
        return minDepth;
    }

    void dep(TreeNode root){
        if(root == null) return ;
        // 递归开始，深度增加
        depth++;
        // 该位置表示递归到叶子节点了，需要更新最小深度minDepth.( 最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。什么是叶子节点，左右孩子都为空的节点才是叶子节点！)
        if(root.left == null && root.right == null)
            minDepth = Math.min(minDepth , depth);
        dep(root.left);
        dep(root.right);
        // 递归结束，深度减小
        depth--;
    }
}

最近公共祖先(重要)

  • https://programmercarl.com/0236.二叉树的最近公共祖先.html#算法公开课
  • 自底向上查找就好了，这样就可以找到公共祖先了。那么二叉树如何可以自底向上查找呢？回溯啊，二叉树回溯的过程就是从低到上。后序遍历（左右中）就是天然的回溯过程，可以根据左右子树的返回值，来处理中节点的逻辑。
  • 如何判断一个节点是节点q和节点p的公共祖先呢? 判断逻辑是 如果递归遍历遇到q，就将q返回，遇到p 就将p返回，那么如果 左右子树的返回值都不为空，说明此时的中节点，一定是q 和p 的最近祖先。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) { 
            return null;  // 递归结束条件: found nothing
        }
        if (root == p || root == q) {
            return root;  // // 递归结束条件 found p or q
        }
        // post order traverse
        TreeNode leftResult = lowestCommonAncestor(root.left, p, q);  // search left subtree
        TreeNode rightResult = lowestCommonAncestor(root.right, p, q);  // search right subtree
         
        if (leftResult != null && rightResult != null) {
            return root; // Found both p and q in the left subtree and the right subtree.
        } else if (leftResult != null && rightResult == null) {
            return leftResult; // Found p or q int the right subtree
        } else if (leftResult == null && rightResult != null) {
            return rightResult; 
        } else {
            return null;  // found nothing in left subtree and right subtree
        }
    }
}

二叉搜索树-诀窍(重要)

  • 二叉搜索树的中序遍历是个递增有序数组, 利用好这一点非常方便解题
  • 二叉搜索树的迭代遍历很好写, 大多数时候用不到递归方式来解题
  • 空二叉树是二叉搜索树

回溯

诀窍与模板

  • 回溯本质是dfs, 所以回溯的模板和图论的dfs模板极为类似
  • https://programmercarl.com/回溯算法理论基础.html#理论基础
  • 起名: 在回溯算法中，我的习惯是函数起名字为backtrack，这个起名大家随意。
  • 返回值: 回溯算法中函数返回值一般为void。
  • 参数: 因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。
1
2
3
4
5
6
7
8
9
10
11
12
void backtrack(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合

没有剪枝的版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
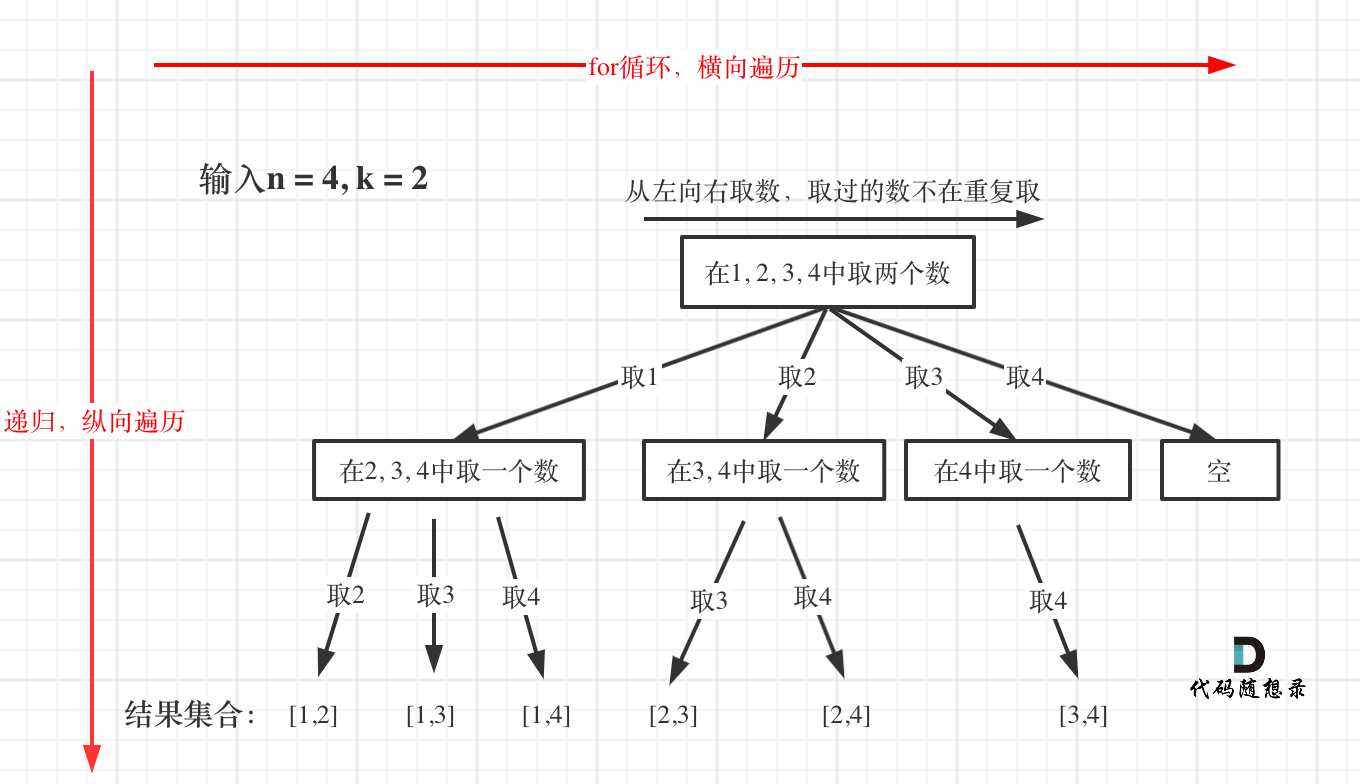
50
class Solution {
    // ArrayList<ArrayList<Integer>> resultArr = new ArrayList<>();和    ArrayList<ArrayList<Integer>> resultArr = new ArrayList<ArrayList<Integer>>();有啥区别? 
    // 完全等价的, `ArrayList<ArrayList<Integer>> resultArr = new ArrayList<>();`
    // - 这是Java 7引入的“钻石操作符”的用法。
    // - 使用钻石操作符可以简化泛型类型的实例化，特别是当构造函数右侧的类型已经由变量声明时。
    // - 它允许编译器自动推断出泛型类型参数，从而使代码更简洁、易读。//解法2：基于小顶堆实现
    public int[] topKFrequent2(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>(); //key为数组元素值,val为对应出现次数
        for (int num : nums) {
            map.put(num, map.getOrDefault(num, 0) + 1);
        }
        //在优先队列中存储二元组(num, cnt),cnt表示元素值num在数组中的出现次数
        //出现次数按从队头到队尾的顺序是从小到大排,出现次数最低的在队头(相当于小顶堆)
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair1[1] - pair2[1]);
        for (Map.Entry<Integer, Integer> entry : map.entrySet()) { //小顶堆只需要维持k个元素有序
            if (pq.size() < k) { //小顶堆元素个数小于k个时直接加
                pq.add(new int[]{entry.getKey(), entry.getValue()});
            } else {
                if (entry.getValue() > pq.peek()[1]) { //当前元素出现次数大于小顶堆的根结点(这k个元素中出现次数最少的那个)
                    pq.poll(); //弹出队头(小顶堆的根结点),即把堆里出现次数最少的那个删除,留下的就是出现次数多的了
                    pq.add(new int[]{entry.getKey(), entry.getValue()});
                }
            }
        }
        int[] ans = new int[k];
        for (int i = k - 1; i >= 0; i--) { //依次弹出小顶堆,先弹出的是堆的根,出现次数少,后面弹出的出现次数多
            ans[i] = pq.poll()[0];
        }
        return ans;
    }
}
    ArrayList<ArrayList<Integer>> resultArr = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public ArrayList<ArrayList<Integer>> combine(int n, int k) {
        backTracking(n, k, 1);
        return resultArr;
    }

    void backTracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            resultArr.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n; ++i) {
            path.add(i);
            backTracking(n, k, i+1);
            path.removeLast();
        }
    }
}

剪枝的版本

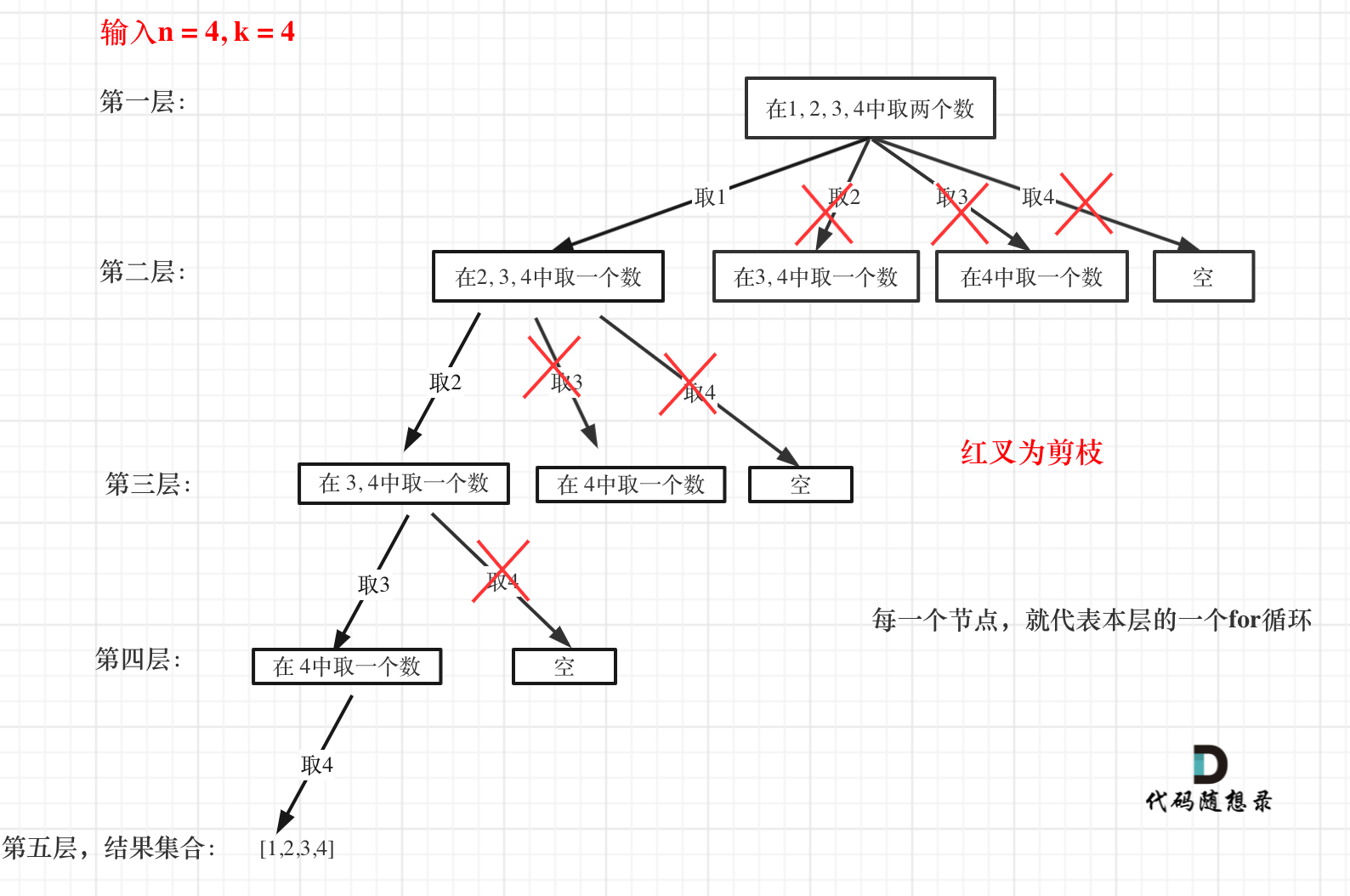
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

注意代码中i，就是for循环里选择的起始位置。

for (int i = startIndex; i <= n; i++) {

接下来看一下优化过程如下：

  • 已经选择的元素个数：path.size();
  • 还需要的元素个数为:k - path.size();
  • 在集合n中i最大可以从该起始位置开始遍历 : n - (k - path.size()) + 1 (备注: n - (k - path.size()) 就是表示从已经最大的数n往回退几个数再开始搜索遍历, 退几个数呢? 退 k - path.size() 个数, 后面多出来的那个 +1是因为要包括起始位置，我们要是一个左闭的集合)

那为什么 n - (k - path.size()) + 1 有个+1呢? 因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0个（即path.size()为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。从”3”开始就不合理了, 因为只能[3, 4, ?], “4”后面没有了, 只有2个数字”3”和”4”能用.

这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。

所以优化之后的for循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

优化后整体代码 diff 如下：

java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    ArrayList<ArrayList<Integer>> resultArr = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public ArrayList<ArrayList<Integer>> combine(int n, int k) {
        backTracking(n, k, 1);
        return resultArr;
    }
    void backTracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            resultArr.add(new ArrayList<>(path));
            return;
        }
-       for (int i = startIndex; i <= n; ++i) {
+       for (int i = startIndex; i <= n - (k - path.size()) + 1; ++i) {
            path.add(i);
            backTracking(n, k, i+1);
            path.removeLast();
        }
    }
}

图论

诀窍

  • dfs一般用来解决 求所有可达路径 问题

    • 代码框架很类似回溯的代码框架, 因为回溯其实就是在做dfs
      图论dfs框架
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      void dfs(参数) {
          if (终止条件) {
              存放结果;
              return;
          }

          for (选择：本节点所连接的其他节点) {
              处理节点;
              dfs(图，选择的节点); // 递归
              回溯，撤销处理结果
          }
      }

  • bfs一般用来解决 求最短路径 问题

    • 只要BFS只要搜到终点一定是一条最短路径, 因为是一层一层一圈一圈来搜的, 搜到的就一定是最短的
    • 代码框架很类似二叉树的bfs, 如下:
      图论bfs框架
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
      // grid 是地图，也就是一个二维数组
      // visited标记访问过的节点，不要重复访问
      // x,y 表示开始搜索节点的下标
      void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
          queue<pair<int, int>> que; // 定义队列
          que.push({x, y}); // 起始节点加入队列
          visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
          while(!que.empty()) { // 开始遍历队列里的元素
              pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
              int curx = cur.first;
              int cury = cur.second; // 当前节点坐标
              for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
                  int nextx = curx + dir[i][0];
                  int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
                  if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过
                  if (!visited[nextx][nexty]) { // 如果节点没被访问过
                      que.push({nextx, nexty});  // 队列添加该节点为下一轮要遍历的节点
                      visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
                  }
              }
          }
      }