algo na

Posted on | In

算法白话总结

参考: https://programmercarl.com/
推荐参考本博客总结的 algo_newbie , 和本文对照着看

概绍

本群的每日刷题打卡活动, 按照 GitHub 49k star的项目 https://github.com/youngyangyang04/leetcode-master 的刷题顺序.
跟着群里有个伴一起刷题或许更容易坚持达成每日一题的目标. 做完题目之后可以在群里的小程序”今日leetcode刷题打卡”里打卡.

  • 网页版: 代码随想录 https://programmercarl.com/
  • 本博客只记录那些有明显自我疑问而<<代码随想录>>没有说明清楚的题目, 会标识出来并注释

本文完整参考代码

https://github.com/no5ix/no5ix.github.io/blob/source/source/code/test_algo_na.java

. . .

数组

lc704 - 二分查找 - 20240814

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
    public int search(int[] numbers, int targetNumber) {
        if (targetNumber < numbers[0] || targetNumber > numbers[numbers.length - 1]) {
            return -1;
        }
        int leftIndex = 0;
        int rightIndex = numbers.length - 1;
        while (leftIndex <= rightIndex) {  // 因为我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right], 所以要使用 <= ，因为left == right是有意义的
        
            /*
            url: https://stackoverflow.com/questions/27167943/why-leftright-left-2-will-not-overflow
            Q: why left+(right-left)/2 can avoid overflow?
            A: 
                Suppose (to make the example easier) the maximum integer is 100, left = 50, and right = 80. If you use the naive formula:

                int mid = (left + right)/2;
                the addition will result in 130, which overflows.

                If you instead do:

                int mid = left + (right - left)/2;
                you can't overflow in (right - left) because you're subtracting a smaller number from a larger number. That always results in an even smaller number, so it can't possibly go over the maximum. E.g. 80 - 50 = 30.

                WWWWasp said: Since (right - left) is the distance between left and right, so `left + (right - left)/2` will not be larger than the right. Furthermore, it will not be larger than the maximum integer.
            */
            int midIndex = leftIndex + ((rightIndex - leftIndex) >> 1);  // >> 1 等同于 除以 2
            if (numbers[midIndex] == targetNumber) {
                return midIndex;
            } else if (numbers[midIndex] < targetNumber) {
                leftIndex = midIndex + 1;
            } else {
                rightIndex = midIndex - 1;
            }
        }
        return -1;
    }
}

public class test{
    public static void main(String[] args){
        Solution solution = new Solution();
        int[] myList = {1, 2, 3, 5, 6, 7, 8, 9, 11};
        int ret = solution.search(myList, 7);
        System.out.println(ret);
    }
}

lc977 - 有序数组的平方 - 20240916

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {  // lc977
    public int[] sortedSquares(int[] nums) {
        int[] resultArray = new int[nums.length];
        int startIndex = 0;
        int endIndex = nums.length - 1;
        int resultIndex = nums.length - 1;
        while (startIndex <= endIndex) {  // 这里是 <= , 因为最后相等时候的那个元素也要处理
            if (nums[startIndex] * nums[startIndex] > nums[endIndex] * nums[endIndex]) {
                resultArray[resultIndex--] = nums[startIndex] * nums[startIndex];
                startIndex++;
            } else {
                resultArray[resultIndex--] = nums[endIndex] * nums[endIndex];
                endIndex--;
            }
        }
        return resultArray;
    }
}

public class test{
    public static void main(String[] args){
        Solution solution = new Solution();
        int[] myList = {-7, 2, 3, 5, 6};
        int[] ret = solution.sortedSquares(myList);
        System.out.println(ret);
        for (int i = 0; i < ret.length; ++i) {
            System.out.println(ret[i]);
        }
    }
}

字符串

lc28 - 实现strStr() - 20240923 - KMP

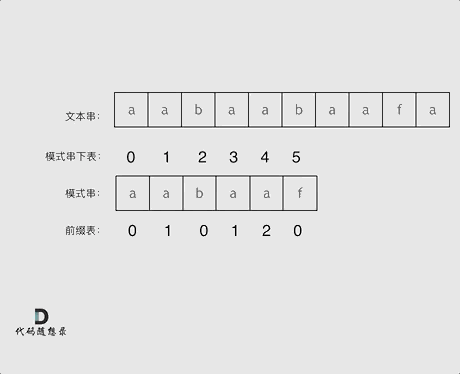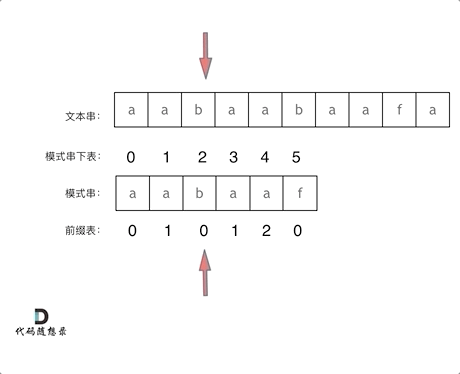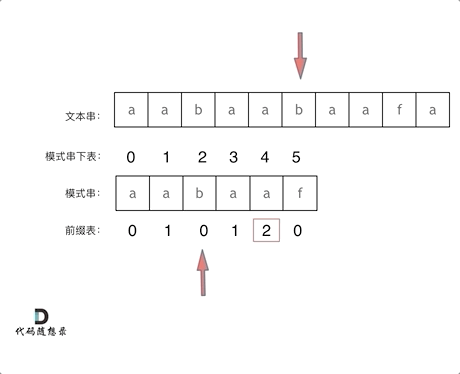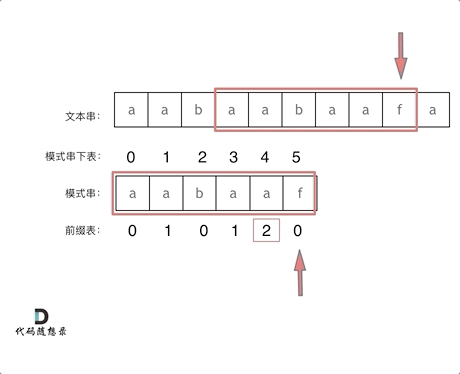
看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如上动画所示：

找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。

为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀。

所以要看前一位的 前缀表的数值。

前一个字符的前缀表的数值是2， 所以把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。

最后就在文本串中找到了和模式串匹配的子串了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
class Solution {
    //前缀表（不减一）Java实现
    public int strStr(String haystack, String needle) {
        if (needle.length() == 0) return 0;
        int[] next = new int[needle.length()];  // 前缀表
        getNext(next, needle);

        int j = 0;  // 此处 j 指向 基于模式串 needle 的 内部的起始位置
        for (int i = 0; i < haystack.length(); i++) {  // i 指向 基于文本串 haystack 内部的起始位置。
            while (j > 0 && needle.charAt(j) != haystack.charAt(i)) 
                j = next[j - 1];  // strStr 里匹配过程里的寻找前一位来继续匹配; 不懂的话看视频 https://www.bilibili.com/video/BV1PD4y1o7nd/?vd_source=8a83b38420b65ac33aa101b7754630f6 里的 "使用前缀表的匹配过程" 环节
            if (needle.charAt(j) == haystack.charAt(i)) 
                j++;
            if (j == needle.length())  // 当 j 等于needle 长度的时候, 说明 j 指向了模式串t的末尾的后面，那么就说明模式串t完全匹配文本串s里的某个子串了。
                return i - needle.length() + 1;
        }
        return -1;

    }
    
    private void getNext(int[] next, String s) {
        int j = 0;  // 此处 j 是 前缀 的末尾位置, 也是前缀的长度
        next[0] = 0;
        for (int i = 1; i < s.length(); i++) {  // i 是后缀的末尾位置
            while (j > 0 && s.charAt(j) != s.charAt(i))  // 此时前后缀不相等; (j要保证大于0，因为下面有取j-1作为数组下标的操作
                j = next[j - 1];  // 注意这里，是要找前一位的对应的回退位置了; 为什么这里要找前一位的对应的回退位置呢? 因为和 上面 strStr 里匹配过程里的寻找前一位来继续匹配是一样一样的
            if (s.charAt(j) == s.charAt(i))   // 此时前后缀相等
                j++;
            next[i] = j;  // 因为 j 既是前缀 的末尾位置, 又是前缀的长度, 所以此处直接在 next 表里存下 j
        }
    }
}

二叉树

二叉树递归解法的写法窍门

再来看返回值，递归函数什么时候需要返回值？什么时候不需要返回值？这里总结如下三点：

前序

前序遍历是中左右，每次先处理的是中间节点，那么先将根节点放入栈中，然后将右孩子加入栈，再加入左孩子。

为什么要先加入 右孩子，再加入左孩子呢？ 因为这样出栈的时候才是中左右的顺序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) { return result; }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(node.val);
            if (node.right != null) { stack.push(node.right); }
            if (node.left != null) { stack.push(node.left); }
        }
        return result;
    }
}

中序

中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问，直到到达树左面的最底部，再开始处理节点（也就是在把节点的数值放进result数组中），这就造成了处理顺序和访问顺序是不一致的。

那么在使用迭代法写中序遍历，就需要借用指针的遍历来帮助访问节点，栈则用来处理节点上的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()) {
            if (cur != null) {
                stack.push(cur);
                cur = cur.left;  // 左
            } else {
                cur = stack.pop();
                result.add(cur.val);  // 中
                cur = cur.right;  // 右
            }
        }
        return result;
    }
}

后序

  1. 先序遍历是中左右
  2. 调整代码左右循序
  3. 变成中右左 -> 反转result数组 -> 左右中
  4. 后序遍历是左右中

层序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
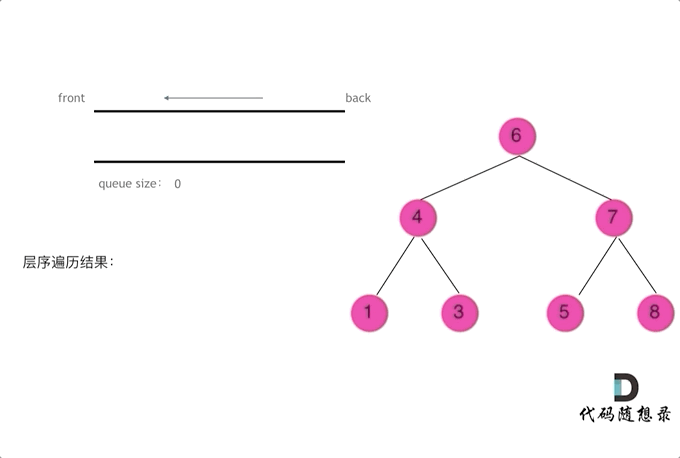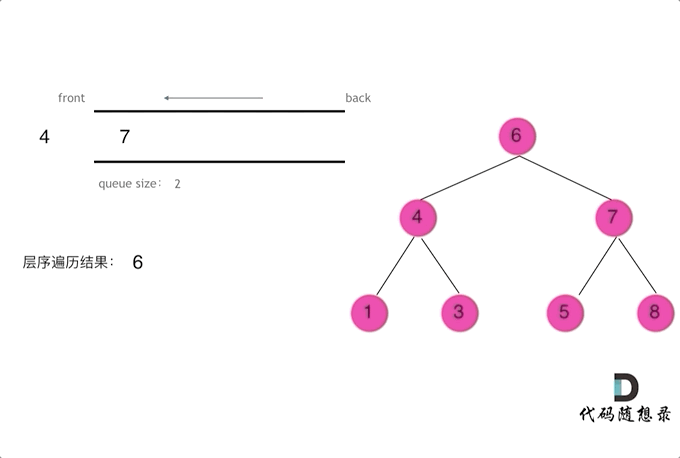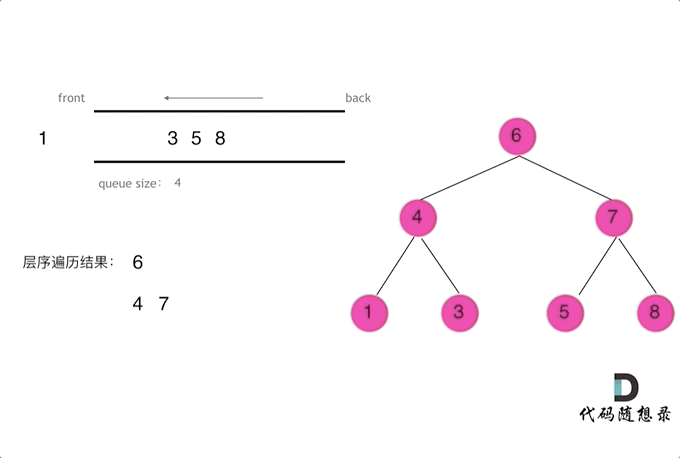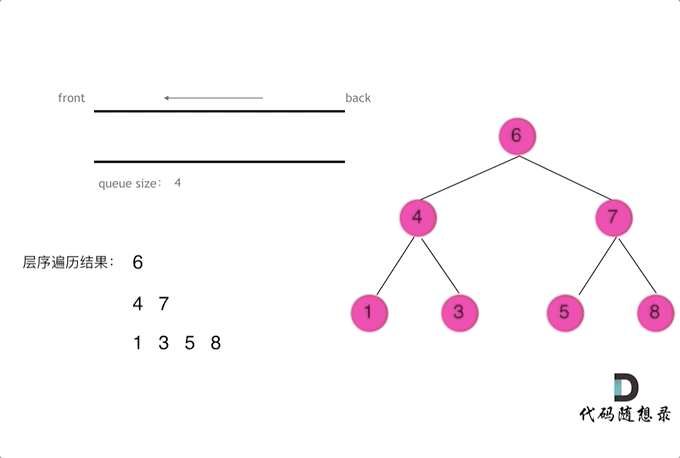
28
class Solution {
    // // 注意返回值是List<List<Integer>>不是单List<Integer>, 因为层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树, 每一层都是一个 List<Integer>, 所以每一层加起来组成一个大的 List<List<Integer>>
    public List<List<Integer>> levelOrder(TreeNode root) {  
        List<List<Integer>> resultList = new ArrayList<List<Integer>>();
        if (root == null ) {
            return resultList;
        }
        Queue<TreeNode> que = new LinkedList<TreeNode>();
        que.offer(root);

        while (!que.isEmpty()) {
            List<Integer> itemList = new ArrayList<Integer>();
            int len = que.size();  // 注意这个len, 这里一定要使用固定大小 len，不要使用que.size()，因为que.size是不断变化的

            while (len > 0) {
                TreeNode tmpNode = que.poll();
                itemList.add(tmpNode.val);

                if (tmpNode.left != null) { que.offer(tmpNode.left); }
                if (tmpNode.right != null) { que.offer(tmpNode.right); }
                len--;
            }
            resultList.add(itemList);
        }

        return resultList;
    }
}

高度

  • 二叉树节点的高度：指从该节点到叶子节点的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）
  • 二叉树节点的深度：指从根节点到该节点的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
  • 而根节点的高度就是二叉树的最大深度

深度

  • 求深度用层序遍历是最适合的最直观容易理解
  • 二叉树的深度: 根节点到最远叶子节点的最长路径上的节点数。
  • 叶子节点: 是指没有子节点的节点。

最大深度

使用迭代法的话，使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。
在二叉树中，一层一层的来遍历二叉树，记录一下遍历的层数就是二叉树的深度，

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int depth = 0;
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        while (!que.isEmpty()) {
            int len = que.size();
            depth++;
            while (len > 0) {
                TreeNode tmpNode = que.poll();
                if (tmpNode.left != null) { que.offer(tmpNode.left); }
                if (tmpNode.right != null) { que.offer(tmpNode.right); }
                len--;
            }
        }
        return depth;
    }
}

最小深度

最小深度: 是从根节点到最近叶子节点的最短路径上的节点数量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int depth = 0;
        Queue<TreeNode> que = new LinkedList<>();
        que.offer(root);
        while (!que.isEmpty()) {
            int len = que.size();
            depth++;
            while (len > 0) {
                TreeNode tmpNode = que.poll();
                if (tmpNode.left == null && tmpNode.right == null) {
                    // 当左右孩子都为空的时候，说明是最低点的一层了，退出
                    return depth;
                }
                if (tmpNode.left != null) { que.offer(tmpNode.left); }
                if (tmpNode.right != null) { que.offer(tmpNode.right); }
                len--;
            }
        }
        return depth;
    }
}

回溯

模板

1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

组合

没有剪枝的版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
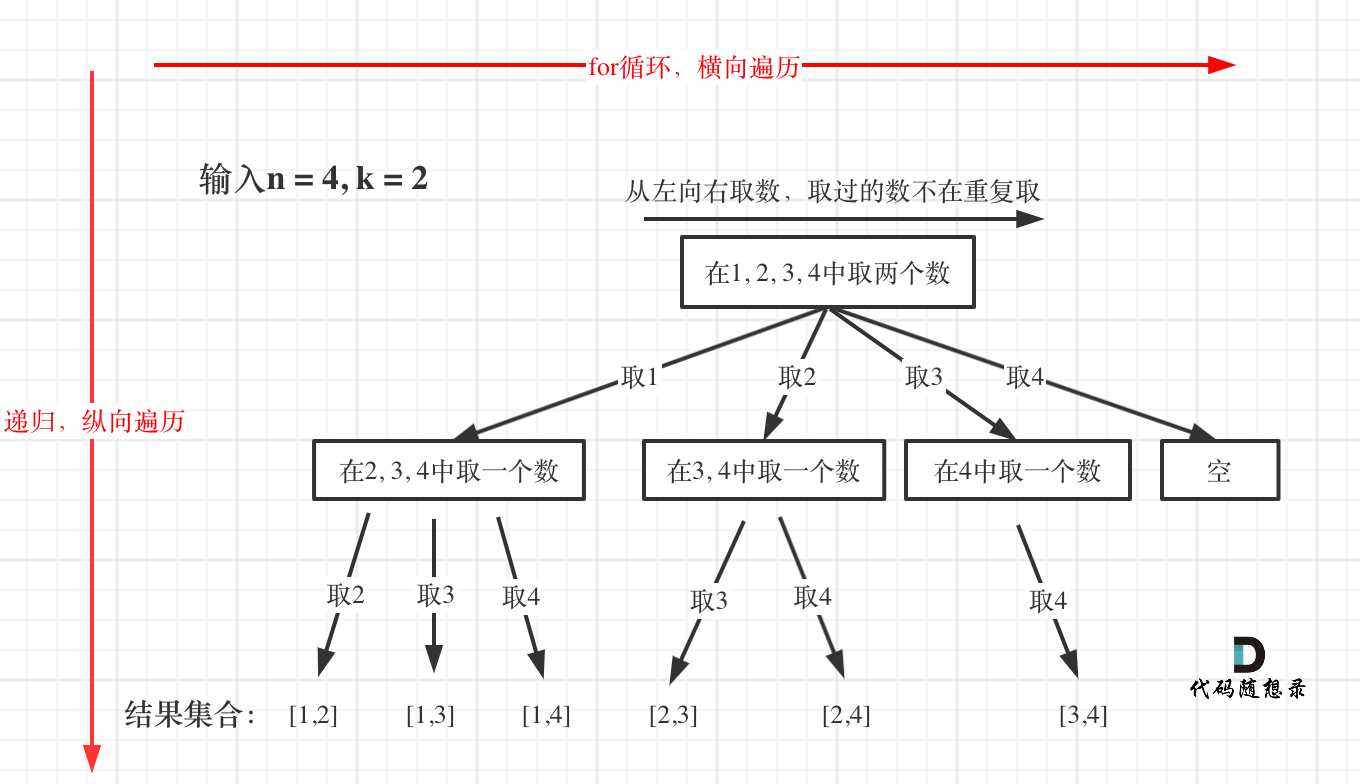
25
class Solution {
    // ArrayList<ArrayList<Integer>> resultArr = new ArrayList<>();和    ArrayList<ArrayList<Integer>> resultArr = new ArrayList<ArrayList<Integer>>();有啥区别? 
    // 完全等价的, `ArrayList<ArrayList<Integer>> resultArr = new ArrayList<>();`
    // - 这是Java 7引入的“钻石操作符”的用法。
    // - 使用钻石操作符可以简化泛型类型的实例化，特别是当构造函数右侧的类型已经由变量声明时。
    // - 它允许编译器自动推断出泛型类型参数，从而使代码更简洁、易读。
    ArrayList<ArrayList<Integer>> resultArr = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public ArrayList<ArrayList<Integer>> combine(int n, int k) {
        backTracking(n, k, 1);
        return resultArr;
    }

    void backTracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            resultArr.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= n; ++i) {
            path.add(i);
            backTracking(n, k, i+1);
            path.removeLast();
        }
    }
}

剪枝的版本

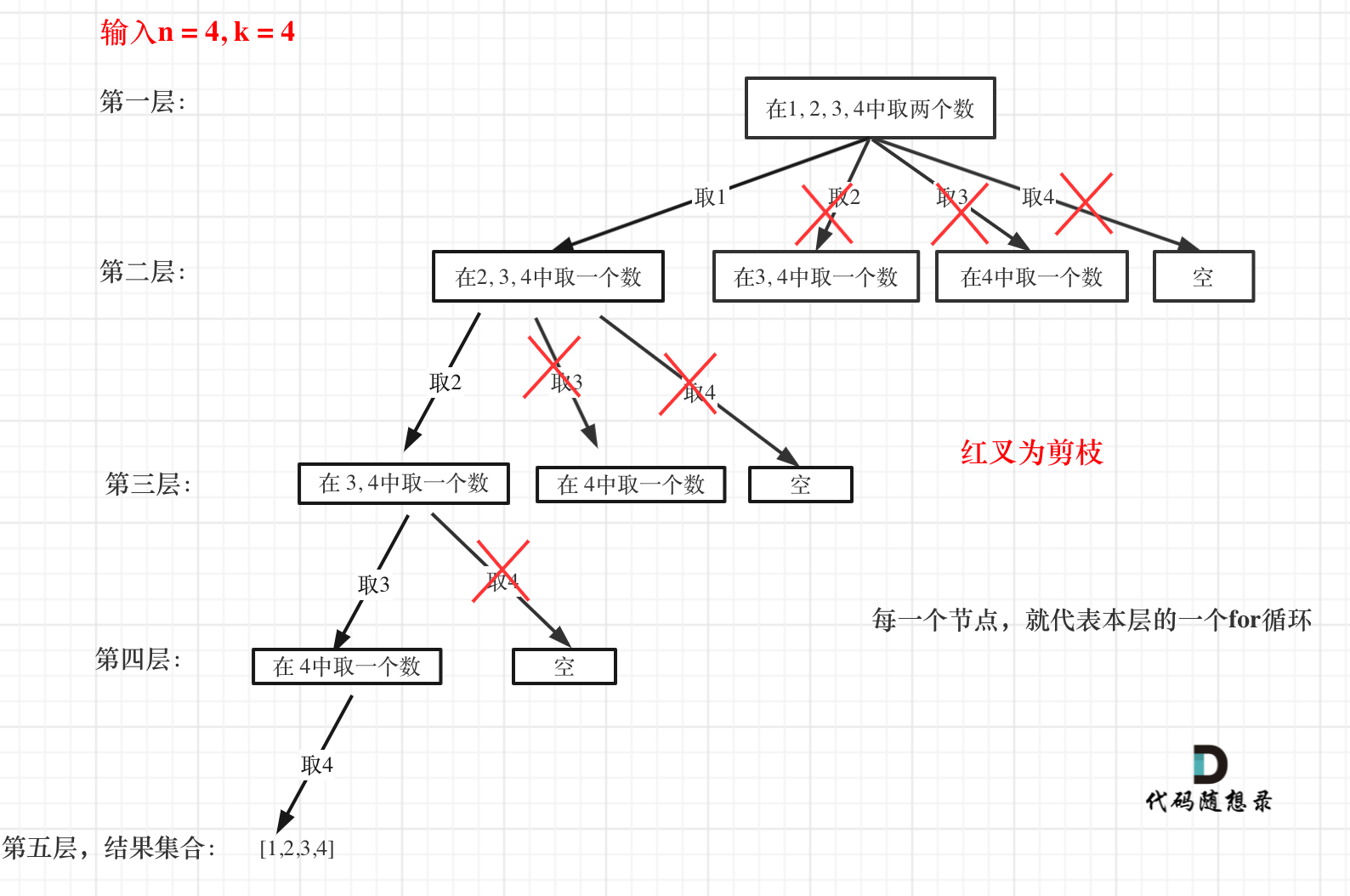
图中每一个节点（图中为矩形），就代表本层的一个for循环，那么每一层的for循环从第二个数开始遍历的话，都没有意义，都是无效遍历。

所以，可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。

如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了，那么就没有必要搜索了。

注意代码中i，就是for循环里选择的起始位置。

for (int i = startIndex; i <= n; i++) {

接下来看一下优化过程如下：

  • 已经选择的元素个数：path.size();
  • 还需要的元素个数为:k - path.size();
  • 在集合n中i最大可以从该起始位置开始遍历 : n - (k - path.size()) + 1 (备注: n - (k - path.size()) 就是表示从已经最大的数n往回退几个数再开始搜索遍历, 退几个数呢? 退 k - path.size() 个数, 后面多出来的那个 +1是因为要包括起始位置，我们要是一个左闭的集合)

那为什么 n - (k - path.size()) + 1 有个+1呢? 因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0个（即path.size()为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。从”3”开始就不合理了, 因为只能[3, 4, ?], “4”后面没有了, 只有2个数字”3”和”4”能用.

这里大家想不懂的话，建议也举一个例子，就知道是不是要+1了。

所以优化之后的for循环是：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置

优化后整体代码 diff 如下：

java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    ArrayList<ArrayList<Integer>> resultArr = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public ArrayList<ArrayList<Integer>> combine(int n, int k) {
        backTracking(n, k, 1);
        return resultArr;
    }
    void backTracking(int n, int k, int startIndex) {
        if (path.size() == k) {
            resultArr.add(new ArrayList<>(path));
            return;
        }
-       for (int i = startIndex; i <= n; ++i) {
+       for (int i = startIndex; i <= n - (k - path.size()) + 1; ++i) {
            path.add(i);
            backTracking(n, k, i+1);
            path.removeLast();
        }
    }
}