算法企业真题实战练习

发表于 | 分类于

算法白话总结

推荐参考本博客总结的 algo_newbie

本文完整参考代码

https://github.com/no5ix/no5ix.github.io/blob/source/source/code/test_algo_practice.py

实战练习 pending_fini

  • 比狗线程排列题
  • 刷完剑指offer
  • 回溯法递归强化

  • 二叉树递归强化

  • lc4题-两个排序数组找中位数, 困难

  • 一个桶里面有白球. 黑球各 100 个，现在按下述的规则取球：
    i . 每次从桶里面拿出来两个球；
    ii. 如果取出的是两个同色的球，就再放入一个黑球；
    iii. 如果取出的是两个异色的球，就再放入一个白球。
    问：最后桶里面只剩下一个黑球的概率是多少？

  • 公司有内部 bbs，员工都会在上面发帖交流。据统计，有三个员工 ID 发帖很多，他们各自的发帖量都超过帖子总数 N 的 1/4。如果给到你所有帖子的发帖人 ID 列表，请写代码找出这三个 ID，要求时间复杂度 O（n），空间复杂度 O（1）。

finished

  • leetcode64题最短路径和
  • 判断是否有一个数num在有序数组中出现次数多于数组长度的一半
    • 判断num是否等于中间的数即可
  • 数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。
    • 根据数组特点得到时间复杂度为O(n)的算法。根据数组特点，数组中有一个数字出现的次数超过数组长度的一半，也就是说它出现的次数比其他所有数字出现的次数之和还要多。因此，我们可以在遍历数组的时候设置两个值：一个是数组中的数result，另一个是出现次数times。当遍历到下一个数字的时候，如果与result相同，则次数加1,不同则次数减一，当次数变为0的时候说明该数字不可能为多数元素，将result设置为下一个数字，次数设为1。这样，当遍历结束后，最后一次设置的result的值可能就是符合要求的值（如果有数字出现次数超过一半，则必为该元素，否则不存在），因此，判断该元素出现次数是否超过一半即可验证应该返回该元素还是返回0。这种思路是对数组进行了两次遍历，复杂度为O(n)。
  • 给定一个含有n个元素的整型数组a，其中只有一个元素出现奇数次，找出这个元素。
    • 解决问题的关键是要想明白，按位异或运算满足结合律，偶数个异或结果是0，奇数个异或结果是本身，如1 ^ 2 ^ 3 ^ 1 ^ 2 ^ 3 ^ 3 = (3 ^ 3 ^ 3) ^ (1 ^ 1) ^ (2 ^ 2) = 3^ 0 ^ 0 = 3。
  • 一个无序数组找其子序列构成的和最大，要求子序列中的元素在原数组中两两都不相邻, 和是多少?具体是哪个子序列?
  • lc445, 两个单向链表，返回求和后的链表结构, 例如2->3->1->5，和3->6，结果返回2->3->5->1
    • 用栈
    • 反转链表再相加

  • 现有一个随机数生成器可以生成0到4的数，现在要让你用这个随机数生成器生成0到6的随机数，要保证生成的数概率均匀。

    • 别被这个题目唬住了, 其实很简单
    • 大多数利用一个等概率随机数构造另外一个等概率随机数的题目，只需两次使用概率函数即可
    • 代码如下:
      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      def rand4():
      	# 这是题目给的
      	pass

      def rand6():
      	res = rand4()
      	# 只要0和1和2, 注意这个0不可少, 不然`res + rand4()`生成的数至少为1
      	while res > 2:
      		res = rand4()
      	# 这样就能保证是等概率0到4 , 等概率的加(0, 1, 2), 得到等概率的0-6
      	return res + rand4()

  • 连续整数求和(leetcode第829题, hard实际有思路就easy)，要求时间复杂度小于O(N)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    class Solution:
       def consecutiveNumbersSum(self, N: int) -> int:
           # 1个数时，必然有一个数可构成N
           # 2个数若要构成N，第2个数与第1个数差为1，N减掉这个1能整除2则能由商与商+1构成N
           # 3个数若要构成N，第2个数与第1个数差为1，第3个数与第1个数的差为2，N减掉1再减掉2能整除3则能由商、商+1与商+2构成N
           # 依次内推，当商即第1个数小于等于0时结束
           res, i = 0, 1
           while N > 0:
               res += N % i == 0
               N -= i
               i += 1
           return res

智力题

  • 有 64 匹马，赛场只有 8 条赛道，请问最少需要比赛多少场才能确定跑得最快的那 4 匹马，不可以借助计时器给每一匹马一一计时；
  • 有 N 枚棋子，每个人一次可以拿1到 M 个，谁拿完后棋子的数量为0谁就获胜。现在有1000颗棋子，每次最多拿8个，A 先拿，那么 A 有必胜的拿法吗？
    • 这个是个智力题不是算法题, 是倍数的思想
    • 这类题得先求得 N % (M+1) 的余数, 此处为 1000 % (8+1) = 1, 求得此余数Y后, 先拿的人第一次就拿Y个, 然后假如B同学第二次拿X个比如是4个, 不管B拿多少个, A之后都拿 (M+1)-X个即 (8+1)-4=5个和B同学拿的4个凑成(8+1)=9个, 这样就保证了A是最后一个拿完棋子的人

misc

寻找第K大

有一个整数数组，请你根据快速排序的思路，找出数组中第K大的数。
给定一个整数数组a,同时给定它的大小n和要找的K(K在1到n之间)，请返回第K大的数，保证答案存在。

测试样例：
[1,3,5,2,2],5,3
返回：2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution_find_top_k_num(object):
    def find_top_k_num(self, nums_arr, nums_arr_len, top_k):
        assert nums_arr, "nums is empty."
        assert nums_arr_len > 0, "nums is empty."
        if top_k > nums_arr_len or top_k < 0:
            return None
        left_index = 0
        right_index = nums_arr_len - 1
        _p_index = self._partition(nums_arr, left_index, right_index)
        while _p_index != top_k-1:
            _p_index = self._partition(nums_arr, left_index, right_index)
            if _p_index < top_k-1:
                left_index = _p_index + 1
            elif _p_index > top_k-1:
                right_index = _p_index - 1
        return nums_arr[_p_index]

    def _partition(self, nums_arr, left_index, right_index):
        pivot_index = left_index
        _partition_index = pivot_index
        for i in range(pivot_index+1, right_index+1):
            if nums_arr[i] <= nums_arr[pivot_index]:
                nums_arr[_partition_index+1], nums_arr[i] = \
                    nums_arr[i], nums_arr[_partition_index+1]
                _partition_index += 1
        nums_arr[_partition_index], nums_arr[pivot_index] = \
            nums_arr[pivot_index], nums_arr[_partition_index]
        return _partition_index

leetcode

lc41-缺失的第一个正数

lc41, hard 缺失的第一个正数（leetcode第41题）
给你一个未排序的整数数组，请你找出其中没有出现的最小的正整数。
示例 1:
输入: [1,2,0]
输出: 3

示例 2:
输入: [3,4,-1,1]
输出: 2

示例 3:
输入: [7,8,9,11,12]
输出: 1

提示：你的算法的时间复杂度应为O(n)，并且只能使用常数级别的额外空间。

参考
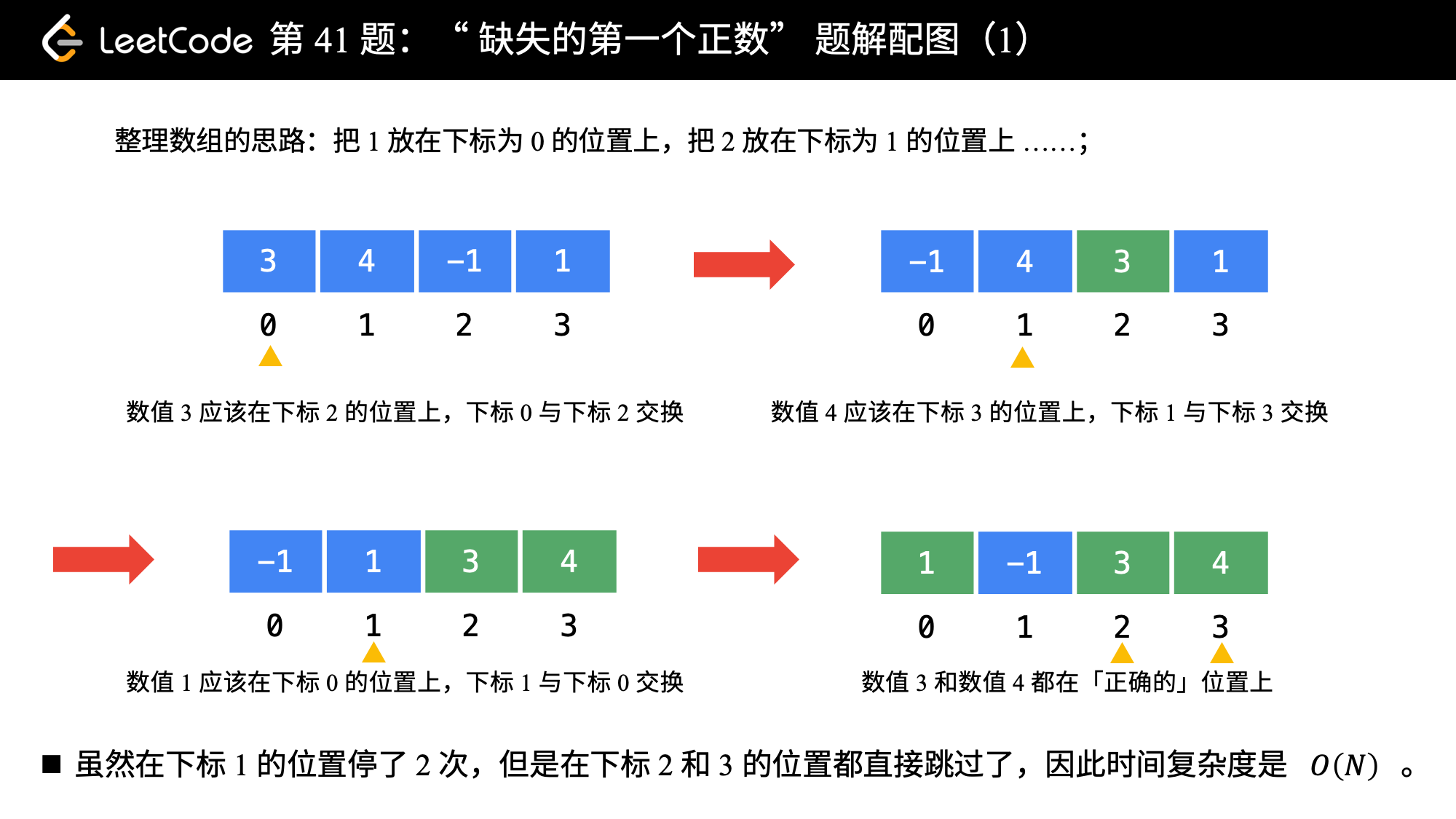
我们可以采取这样的思路：就把 11 这个数放到下标为 00 的位置， 22 这个数放到下标为 11 的位置，按照这种思路整理一遍数组。然后我们再遍历一次数组，第 11 个遇到的它的值不等于下标的那个数，就是我们要找的缺失的第一个正数。
这个思想就相当于我们自己编写哈希函数，这个哈希函数的规则特别简单，那就是数值为 i 的数映射到下标为 i - 1 的位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution_lc41(object):
    def firstMissingPositive(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        思路: 使用座位交换法
        根据题意可知，缺失的第一个整数是在 [1, len + 1] 之间，
        那么我们可以遍历数组，然后将对应的数据填充到对应的位置上去，比如 1 就填充到 nums[0] 的位置， 2 就填充到 nums[1]
        如果填充过程中， nums[i] < 1 && nums[i] > len，那么直接舍弃
        填充完成，我们再遍历一次数组，如果对应的 nums[i] != i + 1，那么这个 i + 1 就是缺失的第一个正数

        比如 nums = [7, 8, 9, 10, 11], len = 5
        我们发现数组中的元素都无法进行填充，直接舍弃跳过，
        那么最终遍历数组的时候，我们发现 nums[0] != 0 + 1，即第一个缺失的是 1 

        比如 nums = [3, 1, 2], len = 3
        填充过后，我们发现最终数组变成了 [1, 2, 3]，每个元素都对应了自己的位置，那么第一个缺失的就是 len + 1 == 4
        """ 
        if not nums:
            return 1
        n = len(nums)
        for i in range(n):
            _pending_swap_index = nums[i] - 1
            # 只有在 nums[i] 是 [1, len] 之间的数，并且不在自己应该呆的位置， nums[i] != i + 1 ，
            # 并且 它应该呆的位置没有被相同的值占有（即存在重复值占有）	nums[nums[i] - 1] != nums[i] 的时候才进行交换
            # 为什么使用 while ？ 因为交换后，原本 i 位置的 nums[i] 已经交换到了别的地方，
            # 交换后到这里的新值不一定是适合这个位置的，因此需要重新进行判断交换
            # 如果使用 if，那么进行一次交换后，i 就会 +1 进入下一个循环，那么交换过来的新值就没有去找到它该有的位置
            # 比如 nums = [3, 4, -1, 1] 当 3 进行交换后， nums 变成 [-1，4，3，1]，
            # 此时 i == 0，如果使用 if ，那么会进入下一个循环， 这个 -1 就没有进行处理
            while(n >= nums[i] >= 1 and nums[i] != i+1 and \
                    nums[i] != nums[_pending_swap_index]):
                # `nums[i] != nums[_pending_swap_index]` 是为了防止
                # nums[i] 和 nums[_pending_swap_index] 这两个数是相等的导致
                # while死循环
                self._swap(nums, i, _pending_swap_index)
                _pending_swap_index = nums[i] - 1

        for i in range(n):
            if nums[i] != i + 1:
                return i + 1                
        return n + 1
        
    def _swap(self, arr, index1, index2):
        arr[index1], arr[index2] = arr[index2], arr[index1]