algo_newbie

Cache和DB一致性

算法企业真题实战练习

实战练习

推荐参考本博客总结的 算法企业真题实战练习

本文完整参考代码

https://github.com/no5ix/no5ix.github.io/blob/source/source/code/test_algo_newbie.py

. . .

python解题常用标准库模块与函数

• sorted函数, 用来排序, 注意sorted不会更改原有数组, 返回的才是排序好的数组

  • 基本操作: num1 = [2, 1, 3]; sorted_num1 = sorted(num1)
  • 按key排序:

    nums = [ [3,4,5], [3,2,6], [2,2,1] ] 
    sorted_nums = sorted(nums, key=lambda x: x[0])
    # out: [[2, 2, 1], [3, 4, 5], [3, 2, 6]]

• heapq模块, 最小堆

  • heapq有两种方式创建堆，
    • 一种是使用一个空列表，然后使用heapq.heappush(test_heap_list, test_num)函数把值加入堆中，
    • 另外一种就是使用heap.heapify(test_list) 转换列表成为堆结构
  • 如果只是想获取最小值而不是弹出，使用test_heap_list[0]
  • 弹出使用heapq.heappop(test_heap_list)

    import heapq
    
    # 第一种
    """
    函数定义：
    heapq.heappush(heap, item)
        - Push the value item onto the heap, maintaining the heap invariant.
    heapq.heappop(heap)
        - Pop and return the smallest item from the heap, maintaining the heap invariant.
        If the heap is empty, IndexError is raised. To access the smallest item without popping it, use heap[0].
    """
    nums = [2, 3, 5, 1, 54, 23, 132]
    heap = []
    for num in nums:
        heapq.heappush(heap, num)  # 加入堆
    
    print(heap[0])  # 如果只是想获取最小值而不是弹出，使用heap[0]
    print([heapq.heappop(heap) for _ in range(len(nums))])  # 堆排序结果
    # out: [1, 2, 3, 5, 23, 54, 132]
    
    
    # 第二种
    nums = [2, 3, 5, 1, 54, 23, 132]
    heapq.heapify(nums)
    print([heapq.heappop(nums) for _ in range(len(nums))])  # 堆排序结果
    # out: [1, 2, 3, 5, 23, 54, 132]

数据结构

哈希表

发生碰撞的时候的解决方案:

• 拉链表法
• 开放寻址法
  • 
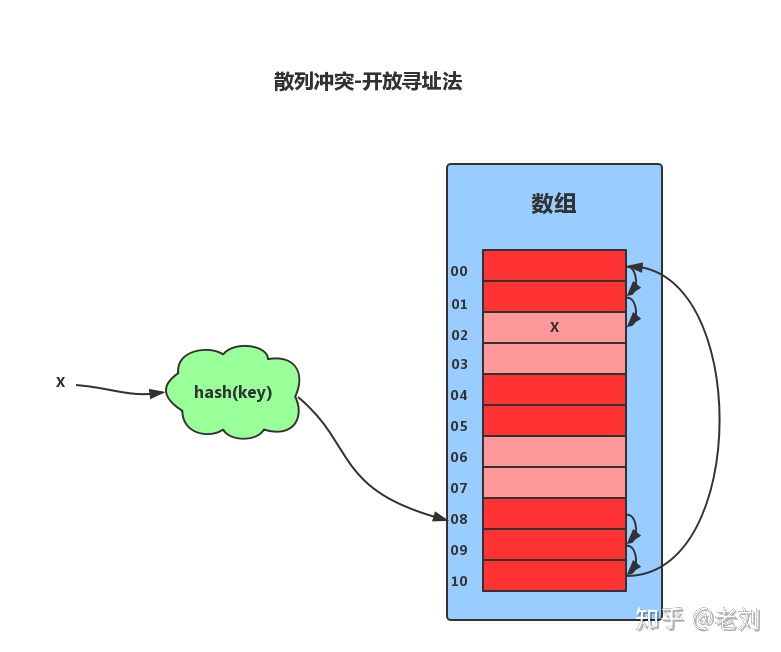
  • 线性探查法, 此法并不好（Linear Probing）：di = 1,2,3,…,m-1
    • 简单地说，就是以当前冲突位置为起点，步长为1循环查找，直到找到一个空的位置，如果循环完了都占不到位置，就说明容器已经满了。举个栗子，就像你在饭点去街上吃饭，挨家去看是否有位置一样。如果遍历到尾部都没有找到空闲的位置，那么我们就再从表头开始找，直到找到为止。
    • 散列表中查找元素的时候，我们通过散列函数求出要查找元素的键值对应的散列值，然后比较数组中下标为散列值的元素和要查找的元素。如果相等，则说明就是我们要找的元素；否则就顺序往后依次查找。如果遍历到数组中的空闲位置还没有找到，就说明要查找的元素并没有在散列表中。
    • 对于删除操作稍微有些特别，不能单纯地把要删除的元素设置为空。因为在查找的时候，一旦我们通过线性探测方法，找到一个空闲位置，我们就可以认定散列表中不存在这个数据。但是，如果这个空闲位置是我们后来删除的，就会导致原来的查找算法失效。这里我们可以将删除的元素，特殊标记为 deleted。当线性探测查找的时候，遇到标记为 deleted 的空间，并不是停下来，而是继续往下探测。
    • 线性探测法存在很大问题。当散列表中插入的数据越来越多时，其散列冲突的可能性就越大，极端情况下甚至要探测整个散列表,因此最坏时间复杂度为O(N)
  • 平方探测法（Quadratic Probing）：di = ±1², ±2², ±3²…，±k²（k≤m/2）
    相对于线性探查法，这就相当于的步长为di = i²来循环查找，直到找到空的位置。以上面那个例子来看，现在你不是挨家去看有没有位置了，而是拿手机算去第i²家店，然后去问这家店有没有位置。
  • 伪随机探测法：di = 伪随机数序列, 这个就是取随机数来作为步长
• 再哈希法
  Hi = RHi(key), 其中i=1,2,…,k
  RHi()函数是不同于H()的哈希函数，用于同义词发生地址冲突时，计算出另一个哈希函数地址，直到不发生冲突位置。这种方法不容易产生堆集，但是会增加计算时间。
  所以再哈希法的缺点是：增加了计算时间。

负载因子与rehash

负载因子计算公式为: 负载因子 = 哈希表已保存节点数量 / 哈希表大小
比如说当前的容器初始容量initCapacity是16，负载因子是0.75(这个负载因子是口语中的负载因子, 实际上指的是该扩容了的负载因子临界值), 根据
元素数量的扩容临界值（threshold） = 负载因子（loadFactor） * 初始容量(initCapacity)
则16*0.75=12，也就是说，当容器中元素数量达到了12的时候就会进行扩容操作。
他的作用很简单，相当于是一个扩容机制的阈值。当超过了这个阈值，就会触发扩容机制。

为什么java的HashMap(使用开放寻址法解决碰撞)负载因子一定是0.75？而不是0.8，0.6？

• loadFactor太大，比如等于1，也就意味着，只有当容器全部填充了，才会发生扩容。那么就会有很高的哈希冲突的概率，会大大降低查询速度。
• loadFactor太小，比如等于0.5，那么频繁扩容没，就会大大浪费空间。

开放寻址法与链表法比较

• 对于开放寻址法解决冲突的散列表:
  • 优势: 由于数据都存储在数组中，因此可以有效地利用 CPU 缓存加快查询速度(数组占用一块连续的空间)。
  • 缺点: 但是删除数据的时候比较麻烦，需要特殊标记已经删除掉的数据。而且，在开放寻址法中，所有的数据都存储在一个数组中，比起链表法来说，冲突的代价更高。所以，使用开放寻址法解决冲突的散列表，负载因子的上限不能太大。这也导致这种方法比链表法更浪费内存空间。
• 对于链表法解决冲突的散列表:
  • 优势:
    • 对内存的利用率比开放寻址法要高。因为链表结点可以在需要的时候再创建，并不需要像开放寻址法那样事先申请好。
    • 链表法比起开放寻址法，对大装载因子的容忍度更高。开放寻址法只能适用装载因子小于1的情况。接近1时，就可能会有大量的散列冲突，性能会下降很多。但是对于链表法来说，只要散列函数的值随机均匀，即便装载因子变成10，也就是链表的长度变长了而已，虽然查找效率有所下降，但是比起顺序查找还是快很多。
  • 缺点: 但是，链表因为要存储指针，所以对于比较小的对象的存储，是比较消耗内存的，而且链表中的结点是零散分布在内存中的，不是连续的，所以对CPU缓存是不友好的，这对于执行效率有一定的影响。

跳表

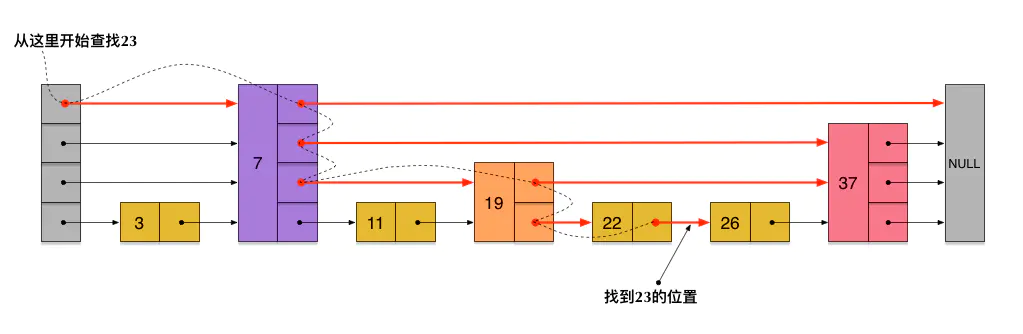
跳表增加数据时索引怎么变化

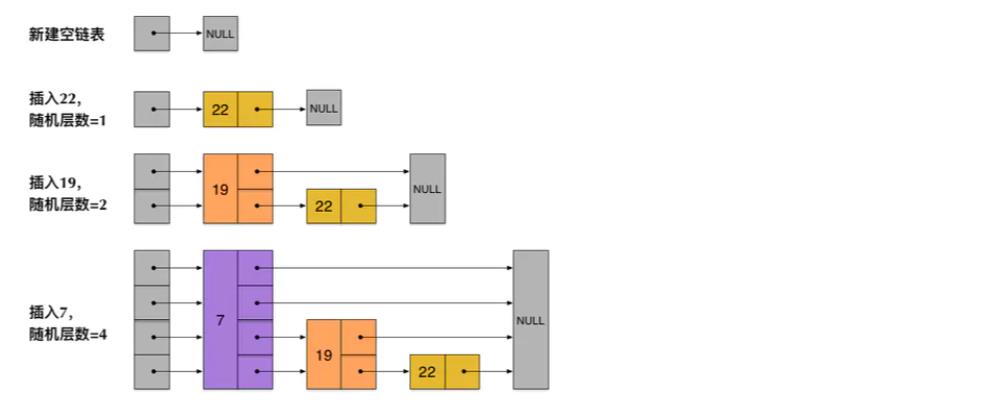
从上面skiplist的创建和插入过程可以看出，每一个节点的层数（level）是随机出来的，而且新插入一个节点不会影响其它节点的层数。因此，插入操作只需要修改插入节点前后的指针，而不需要对很多节点都进行调整。这就降低了插入操作的复杂度。实际上，这是skiplist的一个很重要的特性，这让它在插入性能上明显优于平衡树的方案。这在后面我们还会提到。

执行插入操作时计算随机数的过程，是一个很关键的过程，它对 skiplist 的统计特性有着很重要的影响。这并不是一个普通的服从均匀分布的随机数，它的计算过程如下：

• 首先，每个节点肯定都有第 1 层指针（每个节点都在第 1 层链表里）。
• 如果一个节点有第 i 层 (i>=1) 指针（即节点已经在第 1 层到第 i 层链表中），那么它有第 (i+1) 层指针的概率为 p。
• 节点最大的层数不允许超过一个最大值，记为 MaxLevel。

这个计算随机层数的伪码如下所示：

randomLevel()
    level := 1
    // random()返回一个[0...1)的随机数
    while random() < p and level < MaxLevel do
        level := level + 1
    return level

randomLevel() 的伪码中包含两个参数，一个是 p，一个是 MaxLevel。在 Redis 的 skiplist 实现中，这两个参数的取值为：

p = 1/4
MaxLevel = 32

跳表怎么支持查询排名的

跳表数据结构里存了一个span值, 它表示当前的指针跨越了多少个节点。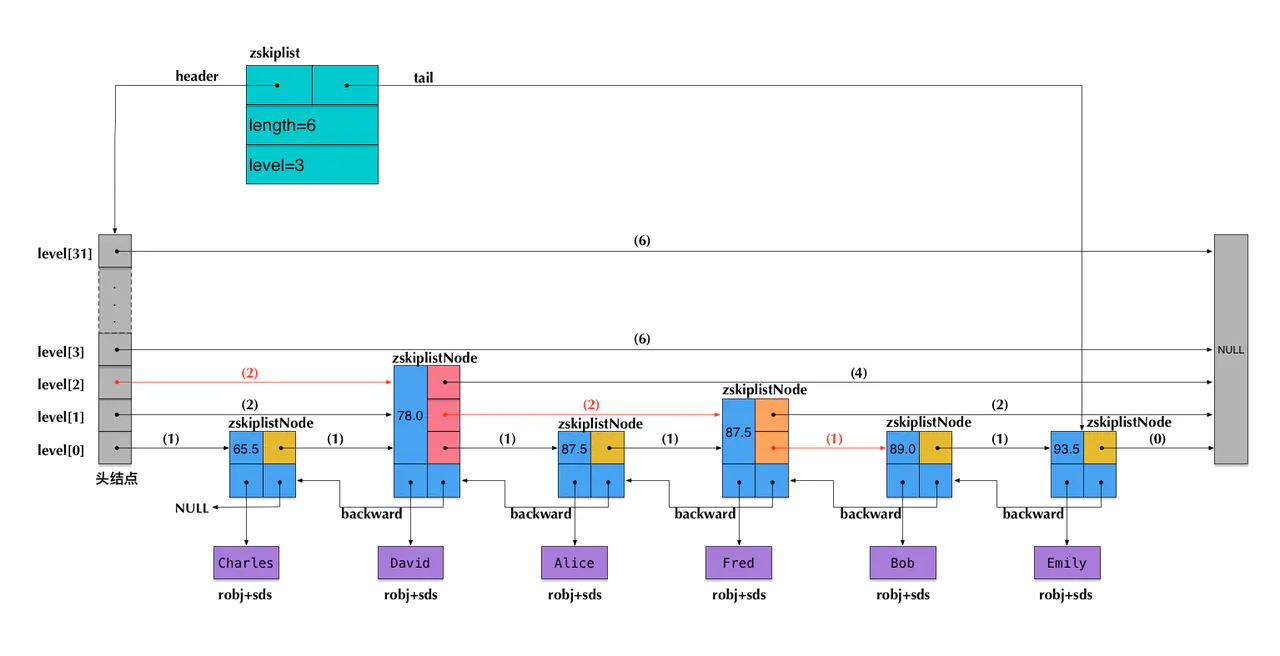

注意：图中前向指针上面括号中的数字，表示对应的span的值。即当前指针跨越了多少个节点，这个计数不包括指针的起点节点，但包括指针的终点节点。
假设我们在这个skiplist中查找score=89.0的元素（即Bob的成绩数据），在查找路径中，我们会跨域图中标红的指针，这些指针上面的span值累加起来，就得到了Bob的排名(2+2+1)-1=4（减1是因为rank值以0起始）。需要注意这里算的是从小到大的排名，而如果要算从大到小的排名，只需要用skiplist长度减去查找路径上的span累加值，即6-(2+2+1)=1。
可见，在查找skiplist的过程中，通过累加span值的方式，我们就能很容易算出排名。相反，如果指定排名来查找数据（类似zrange和zrevrange那样），也可以不断累加span并时刻保持累加值不超过指定的排名，通过这种方式就能得到一条O(log n)的查找路径。

AVL树

AVL树是带有平衡条件的二叉严格平衡查找树，一般是用平衡因子差值判断是否平衡并通过旋转来实现平衡，左右子树树高不超过1，和红黑树相比，它是严格的平衡二叉树，平衡条件必须满足（所有节点的左右子树高度差不超过1）。不管我们是执行插入还是删除操作，只要不满足上面的条件，就要通过旋转来保持平衡，而旋转是非常耗时的，由此我们可以知道AVL树适合用于插入删除次数比较少，但查找多的情况。

红黑树

一种二叉弱平衡查找树，但在每个节点增加一个存储位表示节点的颜色，可以是red或black。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制，红黑树确保没有一条路径会比其它路径长出两倍。它是一种弱平衡二叉树(由于是若平衡，可以推出，相同的节点情况下，AVL树的高度低于红黑树)，相对于要求严格的AVL树来说，它的旋转次数变少，所以对于搜索、插入、删除操作多的情况下，我们就用红黑树。实际应用如下:

• 广泛用于C++的STL中，Map和Set都是用红黑树实现的；
• 著名的Linux进程调度Completely Fair Scheduler，用红黑树管理进程控制块，进程的虚拟内存区域都存储在一颗红黑树上，每个虚拟地址区域都对应红黑树的一个节点，左指针指向相邻的地址虚拟存储区域，右指针指向相邻的高地址虚拟地址空间；
• IO多路复用epoll的实现采用红黑树组织管理sockfd，以支持快速的增删改查；
• Nginx中用红黑树管理timer，因为红黑树是有序的，可以很快的得到距离当前最小的定时器；

B树和B+树

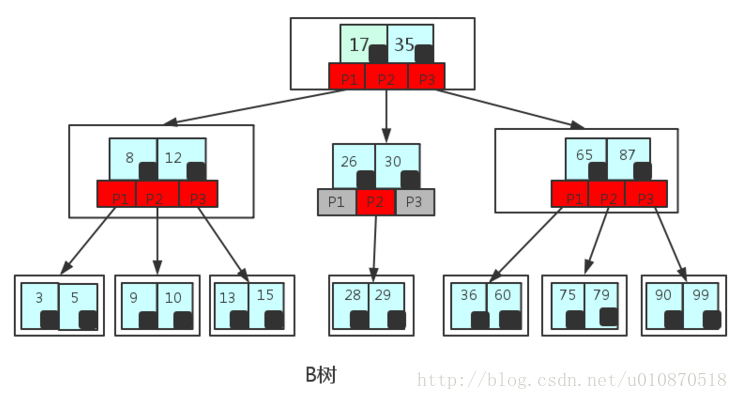
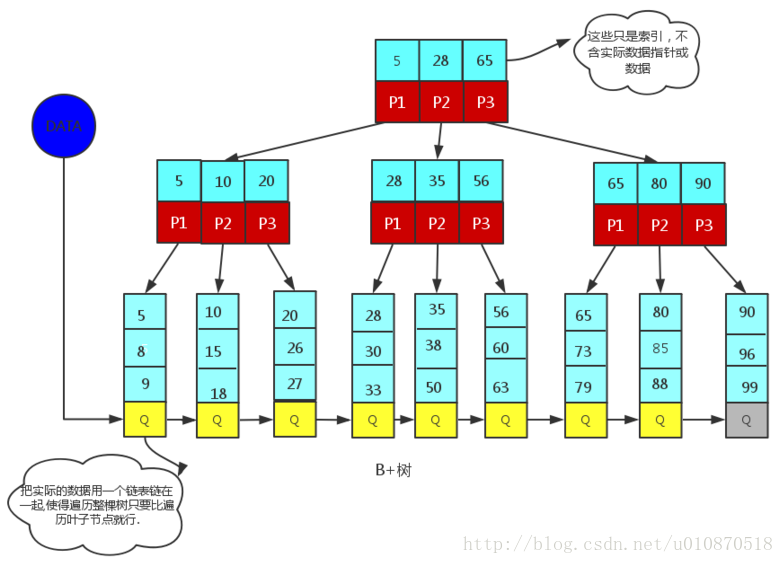
• B树(也叫B-树, 这个-只是个符号…不是B减树哈)
• B+树: B+树是应文件系统所需而产生的一种B树的变形树（文件的目录一级一级索引，只有最底层的叶子节点（文件）保存数据）非叶子节点只保存索引，不保存实际的数据，数据都保存在叶子节点中，所有叶子节点都有一个链表指针把实际的数据用链表连在一起使得遍历整棵树只需要遍历叶子节点就行.

为什么说B类树更适合数据库索引

参考: 为什么MySQL数据库索引选择使用B+树?

• 为什么说B类树更适合数据库索引
  • 我们可以根据B类树的特点，构造一个多阶的B类树，然后在尽量多的在结点上存储相关的信息，保证层数尽量的少，以便后面我们可以更快的找到信息，磁盘的I/O操作也少一些，而且B类树是平衡树，每个结点到叶子结点的高度都是相同，这也保证了每个查询是稳定的。
  • 总的来说，B/B+树是为了磁盘或其它存储设备而设计的一种平衡多路查找树(相对于二叉，B树每个内节点有多个分支)，与红黑树相比，在相同的的节点的情况下，一颗B/B+树的高度远远小于红黑树的高度(在下面B/B+树的性能分析中会提到)。B/B+树上操作的时间通常由存取磁盘的时间和CPU计算时间这两部分构成，而CPU的速度非常快，所以B树的操作效率取决于访问磁盘的次数，关键字总数相同的情况下B树的高度越小，磁盘I/O所花的时间越少。
• 为什么说B+树比B树更适合数据库索引
  • B+树的磁盘读写代价更低：B+树的内部节点并没有指向关键字具体信息的指针，因此其内部节点相对B树更小，如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多，一次性读入内存的需要查找的关键字也就越多，相对IO读写次数就降低了。
  • B+树的查询效率更加稳定：由于b+树非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
  • 由于B+树的数据都存储在叶子结点中，分支结点均为索引，方便扫库，只需要扫一遍叶子结点即可，但是B树因为其分支结点同样存储着数据，我们要找到具体的数据，需要对b树进行一次中序遍历按序来扫，所以B+树更加适合在区间查询的情况，所以通常B+树用于数据库索引。
  • B树在提高了IO性能的同时并没有解决元素遍历的效率低下的问题，正是为了解决这个问题，B+树应用而生。B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作或者说效率太低。

二叉树

• 遍历
  • 深度优先遍历dfs
    • 前序非递归
    • 中序非递归
    • 后序非递归
  • 广度优先遍历bfs
    • 层序遍历
• 非递归反转
• 找普通二叉树的两个结点的最近公共祖先LCA问题
• 二叉搜索树:
  • 它的左、右子树也分别为二叉排序树
  • 其中序遍历是个从小到大的有序序列
  • 找二叉搜索树的任意两个结点的最近公共祖先
    • 在遍历过程中，遇到的第一个值介于n1和n2之间的节点n，也即n1 =< n <= n2, 就是n1和n2的LCA。
    • 在遍历过程中，如果节点的值比n1和n2都大，那么LCA在节点的左子树。
    • 在遍历过程中，如果节点的值比n1和n2都小，那么LCA在节点的右子树。
  • 记住一点, 其中序遍历是一个有序数组, 所以涉及到各种二叉搜索树(如AVL树/红黑树/B树/B+树)总是说要中序遍历扫描结点啥的
    • 类似于 给你一棵所有节点为非负值的二叉搜索树，请你计算树中任意两节点的差的绝对值的最小值 这种题目就可以中序遍历之后得到一个有序数组然后遍历此数组求相邻元素的最小差值即可

二叉树的代码表示:

class TreeNode(object):
    def __init__(self, val):
        self.left = None
        self.right = None
        self.val = val

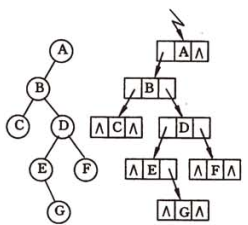
如上图得到的相应的三种深度优先遍历的序列分别为 ：

• 先(根)序遍历 ： ABCDEGF
• 中(根)序遍历 ： CBEGDFA
• 后(根)序遍历 ： CGEFDBA

而得到的广度优先遍历的序列为 : ABCDEFG

统一形式的二叉树前中后序迭代遍历

cpp版本

class TreeNode{
public:
  TreeNode(int _val): val(_val), left(nullptr), right(nullptr) {}
  char val;
  TreeNode *left, *right;
};


void swap_tree(TreeNode *tn){
//   if(tn == nullptr)
//     return;
//   std::cout << tn->val << std::endl;
//   pre_order_traverse(tn->left);
//   pre_order_traverse(tn->right);

//   std::stack<std::pair<const char*, TreeNode*>> st = stack<std::pair<const char*, TreeNode*>>();
  auto st = std::stack<std::tuple<const char*, TreeNode*>>();
  st.push(make_tuple("go", tn));  // todo std::tuple
// //   st.push(make_pair("go", tn));
// 
  while(!st.empty()){
//     auto [cmd, tree_node] = st.top();
//     const char *cmd;
//     TreeNode* tree_node;
//     std::tie(cmd, tree_node) = st.top();
    auto poped_elem = st.top();
    st.pop();
    auto elem = std::get<1>(poped_elem);
    if(strcmp(std::get<0>(poped_elem), "print") == 0){
//       std::cout << std::get<1>(poped_elem)->val << std::endl;
      auto temp = elem->left;
      elem->left = elem->right;
      elem->right = temp;
      continue;
    }
    if(elem->right)
      st.push(make_pair("go", elem->right));
    if(elem->left)
      st.push(make_pair("go", elem->left));
    st.push(make_pair("print", elem));
  }

}


void bfs(TreeNode* tn){
  auto qu = std::queue<TreeNode*>();
  qu.push(tn);

  while (!qu.empty())
  {
    auto front_elem = qu.front();
    qu.pop();
    std::cout << front_elem->val << std::endl;
    if(front_elem->left)
      qu.push(front_elem->left);
    if (front_elem->right)
    {
      qu.push(front_elem->right);
    }
  }
}

python版本

def binary_tree_preorder_traversal(root):
    _result_arr = []
    if not root:
        return _result_arr
    _temp_stack = []
    _temp_stack.append(("go", root))
    while _temp_stack:
        _cmd, _cur_node = _temp_stack.pop(-1)
        if _cmd == "print":
            _result_arr.append(_cur_node.val)
            continue
        if _cur_node.right:
            _temp_stack.append(("go", _cur_node.right))
        if _cur_node.left:
            _temp_stack.append(("go", _cur_node.left))
        _temp_stack.append(("print", _cur_node))
    return _result_arr


def binary_tree_inorder_traversal(root):
    _result_arr = []
    if not root:
        return _result_arr
    _temp_stack = []
    _temp_stack.append(("go", root))
    while _temp_stack:
        _cmd, _cur_node = _temp_stack.pop(-1)
        if _cmd == "print":
            _result_arr.append(_cur_node.val)
            continue
        if _cur_node.right:
            _temp_stack.append(("go", _cur_node.right))
        _temp_stack.append(("print", _cur_node))
        if _cur_node.left:
            _temp_stack.append(("go", _cur_node.left))
    return _result_arr


def binary_tree_postorder_traversal(root):
    _result_arr = []
    if not root:
        return _result_arr
    _temp_stack = []
    _temp_stack.append(("go", root))
    while _temp_stack:
        _cmd, _cur_node = _temp_stack.pop(-1)
        if _cmd == "print":
            _result_arr.append(_cur_node.val)
            continue
        _temp_stack.append(("print", _cur_node))
        if _cur_node.right:
            _temp_stack.append(("go", _cur_node.right))
        if _cur_node.left:
            _temp_stack.append(("go", _cur_node.left))
    return _result_arr

二叉树层序遍历

注意看上图中的文字思路

cpp版本

void bfs(TreeNode* tn){
  auto qu = std::queue<TreeNode*>();
  qu.push(tn);

  while (!qu.empty())
  {
    auto front_elem = qu.front();
    qu.pop();
    std::cout << front_elem->val << std::endl;
    if(front_elem->left)
      qu.push(front_elem->left);
    if (front_elem->right)
    {
      qu.push(front_elem->right);
    }
  }
}

与

python版本

def binary_tree_levelorder_traversal(root):
    _result_arr = []
    if not root:
        return _result_arr
    _temp_queue = []
    _temp_queue.append(root)
    while _temp_queue:
        _cur_node = _temp_queue.pop(0)
        _result_arr.append(_cur_node.val)
        if _cur_node.left:
            _temp_queue.append(_cur_node.left)
        if _cur_node.right:
            _temp_queue.append(_cur_node.right)
    return _result_arr

二叉树反转

值得一提的是，如果把交换左右子节点的代码放在后序遍历的位置也是可以的，但是放在中序遍历的位置是不行的，请你想一想为什么？
因为中序遍历换节点 根据左根右的遍历顺序 相当于左侧节点交换了两次 右侧节点没换 因为遍历根的时候交换了左右节点 遍历右侧的时候还是之前那个左节点, 所以右子树没有被翻转, 以下是递归写法:

def binary_tree_swap_recursive(root):
    if not root:
        return
    root.left, root.right = root.right, root.left
    binary_tree_swap(root.left)
    binary_tree_swap(root.right)

可以看到二叉树反转的递归写法跟前序遍历的递归写法很像,
所以反转的迭代写法也可以对着前序遍历的迭代写法如法炮制:

def binary_tree_swap_iterative(root):
    if not root:
        return
    _temp_stack = []
    _temp_stack.append(("go", root))
    while _temp_stack:
        _cmd, _cur_node = _temp_stack.pop(-1)
        if _cmd == "print":
            # 参考前序遍历的迭代写法, 就只有这里改成了swap操作
            _cur_node.left, _cur_node.right = _cur_node.right, _cur_node.left
            continue
        if _cur_node.right:
            _temp_stack.append(("go", _cur_node.right))
        if _cur_node.left:
            _temp_stack.append(("go", _cur_node.left))
        _temp_stack.append(("print", _cur_node))

链表

链表的代码表示:

class LinkList(object):
    def __init__(self, val):
        self.next = None
        self.val = val

虚头结点的优点:

• 虚头结点是为了操作的统一与方便而设立的，放在第一个元素结点之前，其数据域一般无意义（当然有些情况下也可存放链表的长度、用做监视哨等等）。
• 有了虚头结点后，对在第一个元素结点前插入结点和删除第一个结点，其操作与对其它结点的操作统一了。

常见考题与解题思路

• 可以使用虚头结点来处理问题
• 链表反转
• 虚头节点方便处理问题的思想
• 双指针思想, 适用于下面这种题:
  • 打印倒数第n个结点: 比如链表长度为6, 求打印倒数第3个结点, 则指针p1先走, 走到4的时候, 指针p2才开始走, 这样p1到尾结点的时候, p2刚好再倒数第三个结点
• 快慢指针的思想:
  • 判断链表中是否有环
  • 找一个单链表的中间结点
• 判断两个链表是否相交, 假设两个链表均不带环
  • 最后一个元素必相同
• 给定一个头结点h和结点指针p, 怎么删除该结点
  • 判断是否只有一个结点, 即判断if h == p and not h.next
  • 判断是否为末尾结点, 即判断if not p.next, 是的话还是得从头遍历找到p的前一个结点
  • 如果都不是, 则直接删除p后面的节点b, 并把b的内容复制到p上即可

链表反转

思路:

1. 先设置一个虚头节点 pre,
2. 先暂存好cur的next为temp_next
3. 然后开始用cur去连接他即cur.next = pre,
4. 把暂存好的 temp_next 赋值给 cur, 继续下一轮 while cur: 循环

cpp版本

struct LinkedList;
typedef shared_ptr<LinkedList> llp;

typedef struct LinkedList{
  LinkedList(char _val): val(_val), next(nullptr) {}
  char val;
  llp next;
} ll;

llp reverse_linked_list(llp test_ll){
  if(test_ll == nullptr)
    return test_ll;

  llp head = nullptr;
  auto cur = test_ll;
  while(cur){
    auto temp_next = cur->next;
    cur->next = head;
    head = cur;
    cur = temp_next;
  }
  return head;
}

与

python版本

def linklist_reverse(head):
    if not head:
        return
    _pre = None
    _cur = head
    _temp_next = head.next
    while _cur:
        #先用_temp_next保存_cur的下一个节点的信息，
        #保证单链表不会因为失去_cur节点的next而就此断裂
        _temp_next = _cur.next
        #保存完_temp_next，就可以让_cur的next指向_pre了
        _cur.next = _pre
        #让_pre，_cur依次向后移动一个节点，继续下一次的指针反转
        _pre = _cur
        _cur = _temp_next
    return _pre

图论

• 广度优先遍历dfs可以得到最短路径
• 深度优先遍历bfs有啥用? 图的深度优先遍历dfs

图的表示

下面这个图结构就有三个连通分量: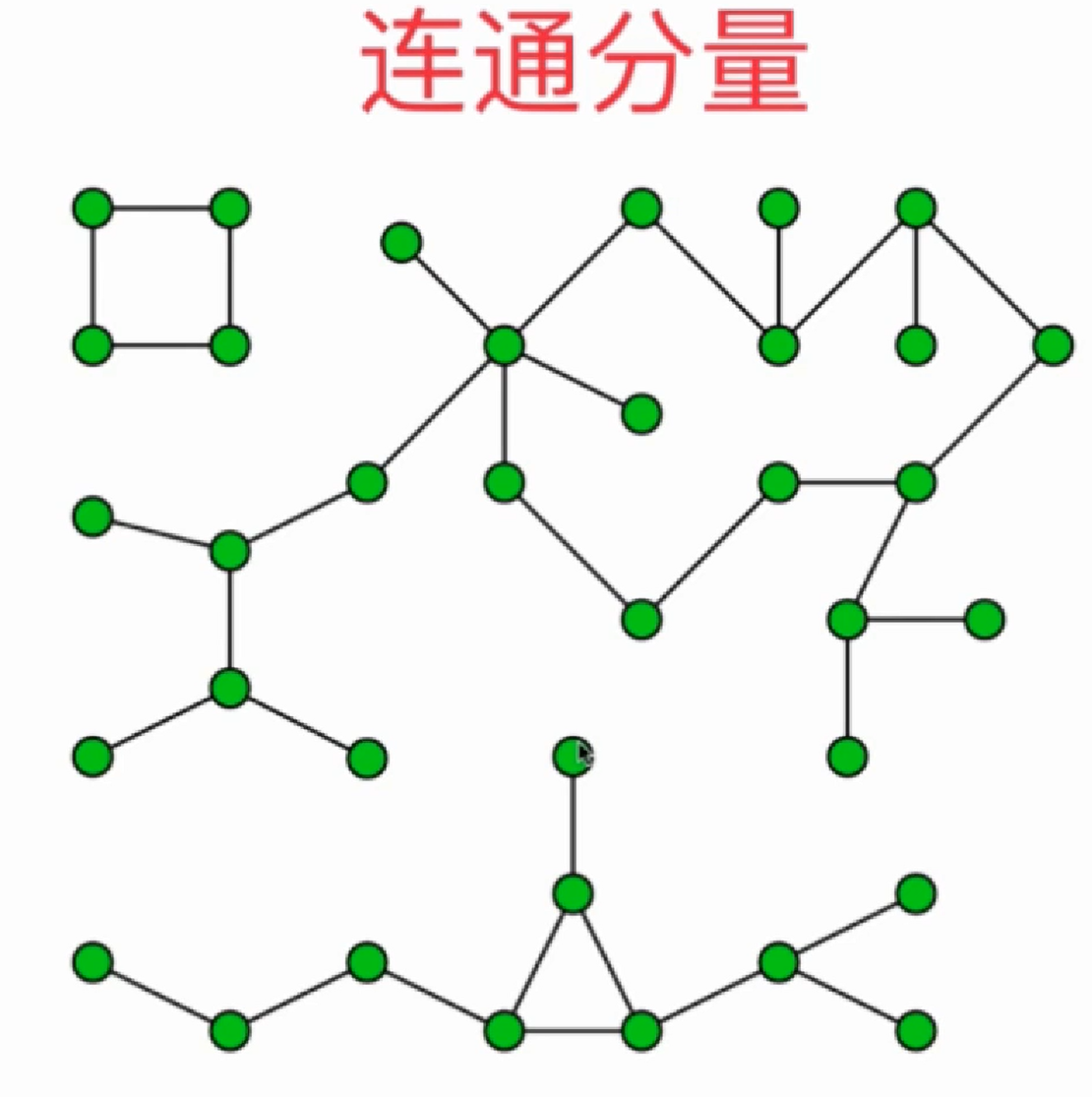

邻接表适合表示稀疏图(Sparse Graph):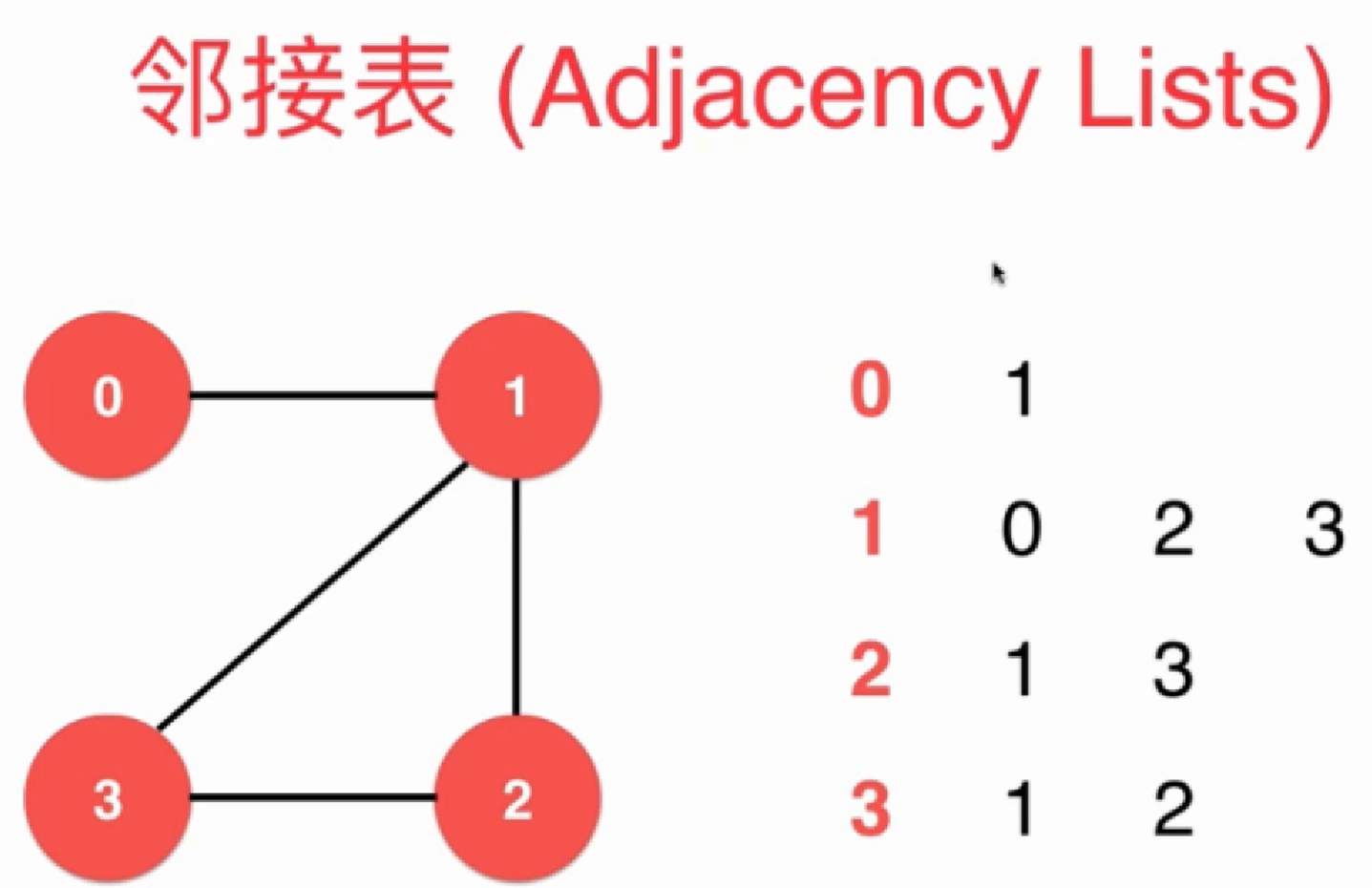

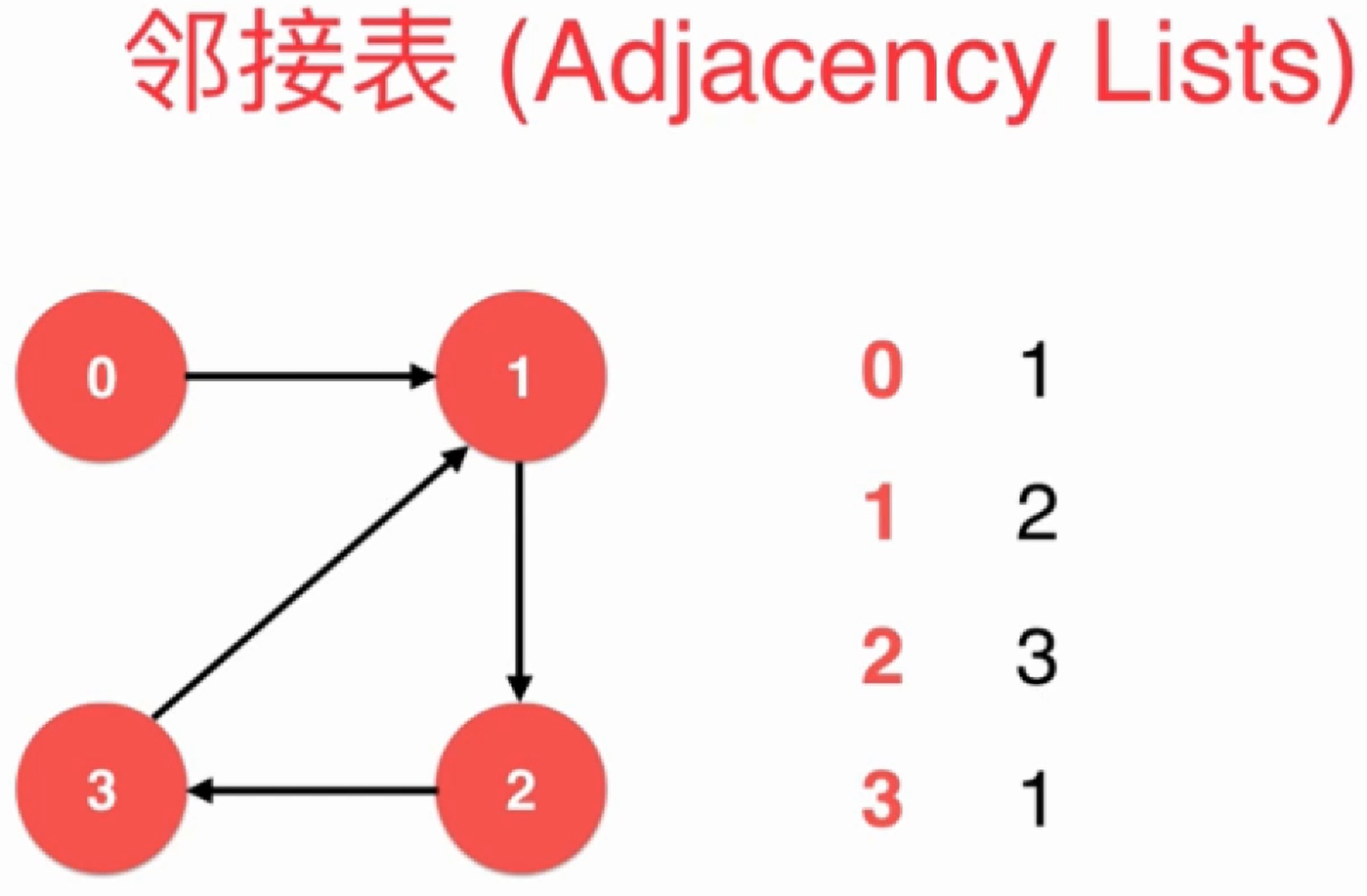
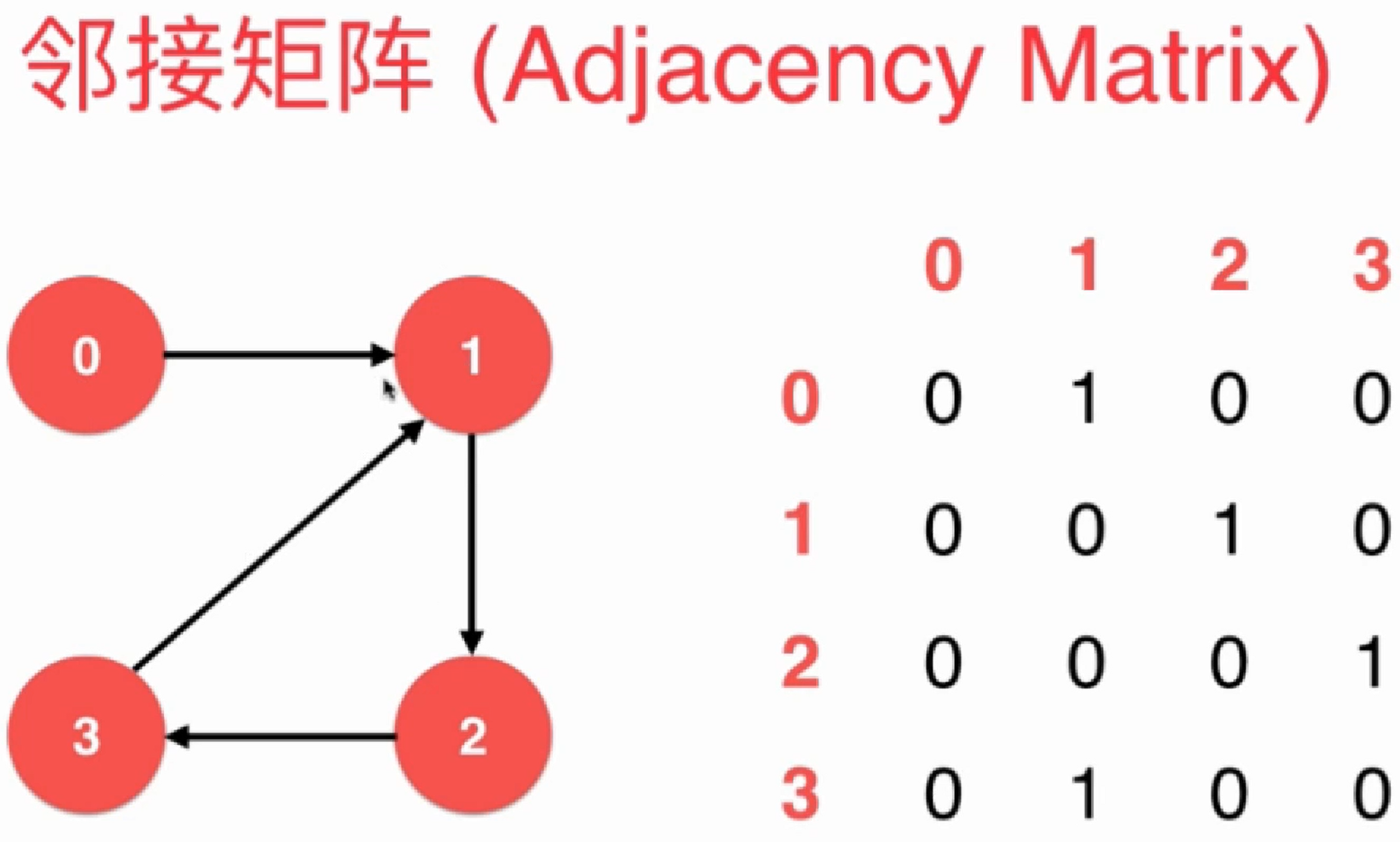
邻接矩阵适合表示稠密图(Dense Graph):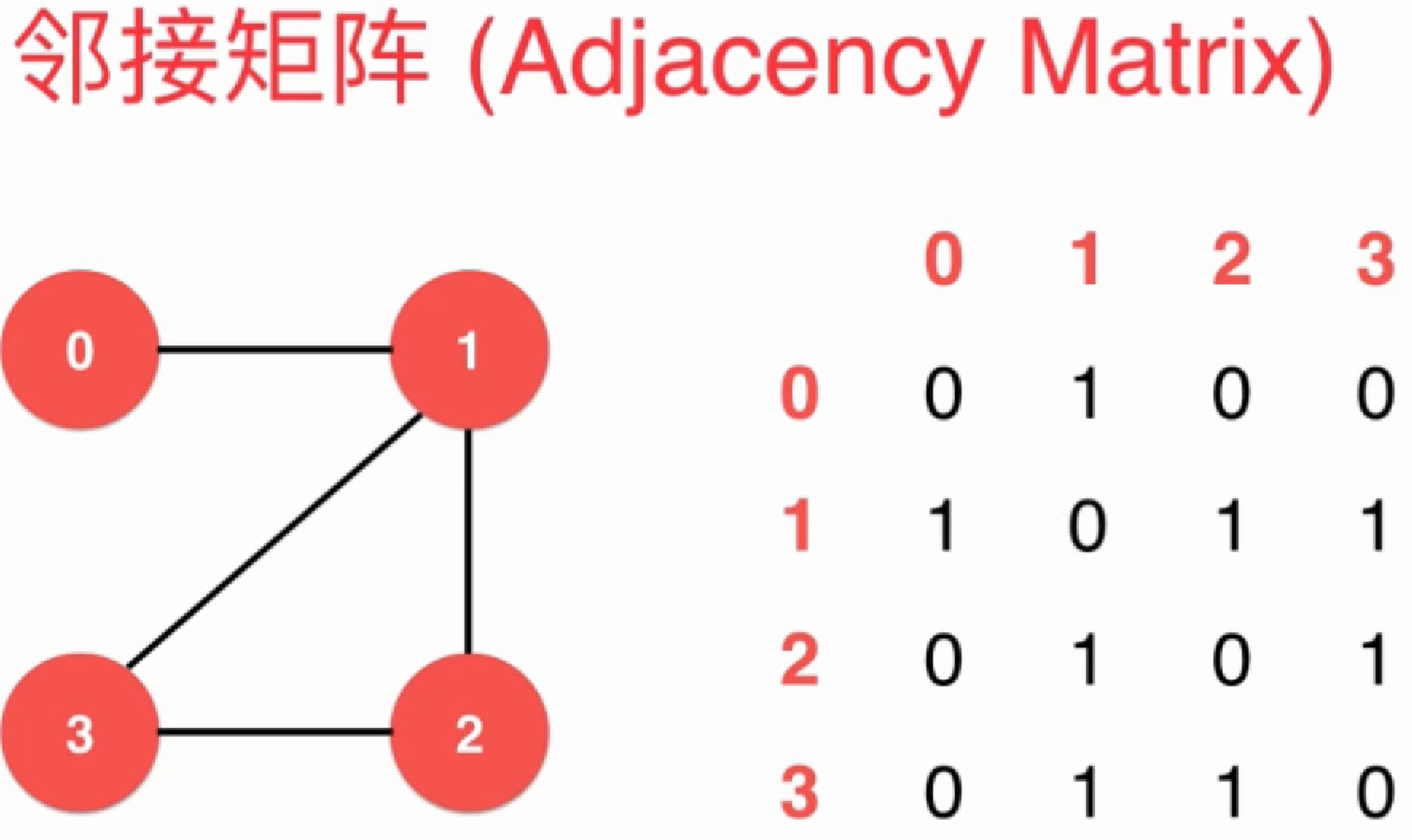

图的代码实现

代码如下:

class GraphBase(object):
    # 图的基类

    def __init__(self, point_count, is_directed):
        # 因为稀疏图一般用邻接表来保存图的顶点数据,
        # 而稠密图一般用邻接矩阵来表示, 所以他们的保存邻接点容器是不同的,
        # 留给具体子类来指定, 此处用 `self.adjacency_container = None`表示即可
        self.adjacency_container = None
        self.is_directed = is_directed  # 是否为有向图
        self.connected_components_count = 0  # 连通分量个数
        self.point_count = point_count

    def graph_dfs(self):
        """
        图的深度优先遍历（DFS）, 深度优先遍历尽可能优先往深层次进行搜索；
        1. 首先访问出发点v，并将其标记为已访问过；
        2. 然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点均已被访问为止。
        3. 若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点为新的源点重复上述过程，直至图中所有的顶点均已被访问为止。
        """
        visited_arr = []
        for _cur_point_index in xrange(0, len(self.adjacency_container)):
            if _cur_point_index not in visited_arr:
                self._dfs_by_point(_cur_point_index, visited_arr)
                # 运行到此处, 说明已经把所有和_cur_point_index 相连接的点都遍历完了,
                # A-B-C 也算作 A和C相连接的,
                # 其他的点肯定在另一个连接分量中
                self.connected_components_count += 1
        return visited_arr

    def _dfs_by_point(self, cur_point_index, visited_arr):
        visited_arr.append(cur_point_index)
        for _next_point_index in self._iter_adjacent_points(cur_point_index):
            if _next_point_index not in visited_arr:
                self._dfs_by_point(_next_point_index, visited_arr)

    def graph_bfs(self):
        """
        图的广度优先遍历, 也可以称为图的层序遍历, 广度优先遍历按层次优先搜索最近的结点，一层一层往外搜索:
        1. 首先访问出发点v，接着依次访问v的所有邻接点w1、w2......wt，
        2. 然后依次访问w1、w2......wt邻接的所有未曾访问过的顶点。
        3. 以此类推，直至图中所有和源点v有路径相通的顶点都已访问到为止。此时从v开始的搜索过程结束。
        4. 若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点为新的源点重复上述过程，直至图中所有的顶点均已被访问为止。
        """
        result_arr = []
        visited_set = set()  # 用来记录某个顶点是否已经访问过
        _temp_queue = []
        for _cur_point_index in xrange(0, len(self.adjacency_container)):
            if _cur_point_index not in visited_set:
                _temp_queue.append(_cur_point_index)
                visited_set.add(_cur_point_index)
            while _temp_queue:
                _pt = _temp_queue.pop(0)
                result_arr.append(_pt)
                for _next_pt_index in self._iter_adjacent_points(_pt):
                    if _next_pt_index not in visited_set:
                        _temp_queue.append(_next_pt_index)
                        visited_set.add(_next_pt_index)
        return result_arr

    def _iter_adjacent_points(self, cur_point_index):
        """
        因为稀疏图一般用邻接表来保存图的顶点数据,
        而稠密图一般用邻接矩阵来表示,
        所以他们的遍历邻接点的方式是不同的, 留给具体的子类来实现.
        """
        raise NotImplementedError

    def add_edge(self, start_point_index, end_point_index):
        raise NotImplementedError


class SparseGraph(GraphBase):
    # 稀疏图

    def __init__(self, point_count, is_directed):
        super(SparseGraph, self).__init__(point_count, is_directed)
        self.adjacency_container = [[] for _ in xrange(point_count)]  # 邻接表
        self.indegree_list = [ 0 for _ in range(point_count) ]  # 每个顶点的入度, 初始化为0

    def set_adjacency_list(self, adjacency_list):
        self.adjacency_container = adjacency_list

    def _iter_adjacent_points(self, cur_point_index):
        for _adjacent_point_index in self.adjacency_container[cur_point_index]:
            yield _adjacent_point_index

    def add_edge(self, start_point_index, end_point_index):
        self.adjacency_container[start_point_index].append(end_point_index)
        self.indegree_list[end_point_index] += 1
        if not self.is_directed:
            self.adjacency_container[end_point_index].append(start_point_index)

    def topologic_sort(self):
        result_arr = []
        zero_indegree_list = []
        for point_index, cur_indegree in enumerate(self.indegree_list):
            if cur_indegree == 0:
                zero_indegree_list.append(point_index)  # 将所有入度为0的顶点加入列表
        while zero_indegree_list:
            cur_point_index = zero_indegree_list.pop()  # 从列表中取出一个顶点
            result_arr.append(cur_point_index)
            # 将所有v指向的顶点的入度减1，并将入度减为0的顶点加入列表
            for j in self.adjacency_container[cur_point_index]:
                self.indegree_list[j] -= 1
                if self.indegree_list[j] == 0:
                    zero_indegree_list.append(j)  # 若入度为0，则加入列表
        if len(result_arr) != self.point_count:
            return False, result_arr  # 没有输出全部顶点，说明有向图中有回路
        else:
            return True, result_arr
            

class DenseGraph(GraphBase):
    # 稠密图

    def __init__(self, point_count, is_directed):
        super(DenseGraph, self).__init__(point_count, is_directed)
        self.adjacency_container = [
            [0 for _ in xrange(point_count)] for _ in xrange(point_count)
        ]  # 邻接矩阵

    def set_adjacency_matrix(self, adjacency_matrix):
        self.adjacency_container = adjacency_matrix

    def _iter_adjacent_points(self, cur_point_index):
        for _adjacent_point_index, _is_point_adjacent in enumerate(self.adjacency_container[cur_point_index]):
            if not _is_point_adjacent:
                continue
            yield _adjacent_point_index

    def add_edge(self, start_point_index, end_point_index):
        self.adjacency_container[start_point_index][end_point_index] = 1
        if not self.is_directed:
            self.adjacency_container[end_point_index][start_point_index] = 1

    def topologic_sort(self):
        pass  # TODO


if __name__ == "__main__":
    temp_adjacency_list = [
        [1, 2, 5, 6],
        [0],
        [0],
        [4, 5],
        [3, 5, 6],
        [0, 3, 4],
        [0, 4],
    ]
    test_sparse_graph = SparseGraph(point_count=len(temp_adjacency_list), is_directed=False)
    test_sparse_graph.set_adjacency_list(temp_adjacency_list)
    print "test_sparse_graph graph dfs:"
    print test_sparse_graph.graph_dfs()
    print "test_sparse_graph graph bfs:"
    print test_sparse_graph.graph_bfs()
    test_sparse_graph = SparseGraph(point_count=6, is_directed=True)
    test_sparse_graph.add_edge(5, 2)
    test_sparse_graph.add_edge(5, 0)
    test_sparse_graph.add_edge(4, 0)
    test_sparse_graph.add_edge(4, 1)
    test_sparse_graph.add_edge(2, 3)
    test_sparse_graph.add_edge(3, 1)
    print "test_sparse_graph topologic_sort: --------------"
    print test_sparse_graph.topologic_sort()

    # 这个邻接矩阵表示的和上面那个邻接表 temp_adjacency_list 是同一个图
    temp_adjacency_matrix = [
        [0, 1, 1, 0, 0, 1, 1],
        [1, 0, 0, 0, 0, 0, 0],
        [1, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 1, 1, 0],
        [0, 0, 0, 1, 0, 1, 1],
        [1, 0, 0, 1, 1, 0, 0],
        [1, 0, 0, 0, 1, 0, 0],
    ]
    test_dense_graph = DenseGraph(point_count=len(temp_adjacency_matrix), is_directed=False)
    test_dense_graph.set_adjacency_matrix(temp_adjacency_matrix)
    print "test_dense_graph graph dfs:"
    print test_dense_graph.graph_dfs()
    print "test_dense_graph graph bfs:"
    print test_dense_graph.graph_bfs()

打印结果:

test_sparse_graph graph dfs:
[0, 1, 2, 5, 3, 4, 6]
test_sparse_graph graph bfs:
[0, 1, 2, 5, 6, 3, 4]
test_sparse_graph topologic_sort: --------------
(True, [4, 5, 2, 0, 3, 1])
test_dense_graph graph dfs:
[0, 1, 2, 5, 3, 4, 6]
test_dense_graph graph bfs:
[0, 1, 2, 5, 6, 3, 4]

图的深度优先遍历dfs

图的深度优先遍历（DFS）, 深度优先遍历尽可能优先往深层次进行搜索；

1. 首先访问出发点v，并将其标记为已访问过；
2. 然后依次从v出发搜索v的每个邻接点w。若w未曾访问过，则以w为新的出发点继续进行深度优先遍历，直至图中所有和源点v有路径相通的顶点均已被访问为止。
3. 若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点为新的源点重复上述过程，直至图中所有的顶点均已被访问为止。

代码在上方已经有了, 其代码中的 graph_dfs 就是.

图dfs用途:

• 可以获得两点之间的一条路径
• 判断图是否有环: pending_fini
  • leetcode原题201与题解
  • 大致算法思想: 一条深度遍历路线中如果有结点被第二次访问到，那么有环。我们用一个变量来标记某结点的访问状态（未访问，访问过，其后结点都被访问过），然后判断每一个结点的深度遍历路线即可。

图的广度优先遍历bfs

也可以称为层序遍历, 广度优先遍历按层次优先搜索最近的结点，一层一层往外搜索:

1. 首先访问出发点v，接着依次访问v的所有邻接点w1、w2……wt，
2. 然后依次访问w1、w2……wt邻接的所有未曾访问过的顶点。
3. 以此类推，直至图中所有和源点v有路径相通的顶点都已访问到为止。此时从v开始的搜索过程结束。
4. 若此时图中仍有未访问的顶点，则另选一个尚未访问的顶点为新的源点重复上述过程，直至图中所有的顶点均已被访问为止。

图的bfs一般要用一个队列来实现, 代码在上方已经有了, 其代码中的 graph_bfs 就是.

图bfs用途:

• 可以获得两点之间的最短路径

拓扑排序

参考
拓扑排序通常用来 “排序” 具有依赖关系的任务.
比如，如果用一个 DAG 图来表示一个工程，其中每个顶点表示工程中的一个任务，用有向边 表示在做任务 B 之前必须先完成任务 A。故在这个工程中，任意两个任务要么具有确定的先后关系，要么是没有关系，绝对不存在互相矛盾的关系（即环路）。

在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

• 每个顶点出现且只出现一次。
• 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非 DAG 图没有拓扑排序一说。例如，下面这个图：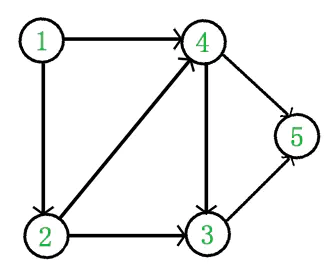

它是一个 DAG 图，那么如何写出它的拓扑排序呢？这里说一种比较常用的方法：

1. 从 DAG 图中选择一个 没有前驱（即入度为 0）的顶点并输出。
2. 从图中删除该顶点和所有以它为起点的有向边。
3. 重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

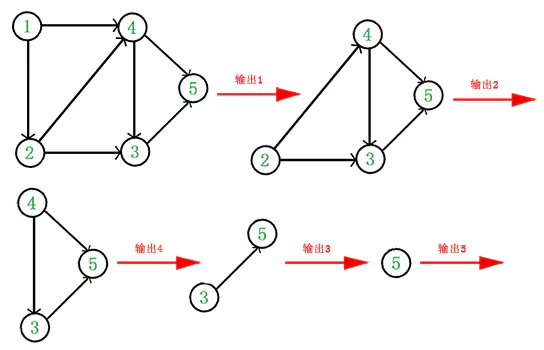
于是，得到拓扑排序后的结果是 {1, 2, 4, 3, 5}。通常，一个有向无环图可以有一个或多个拓扑排序序列。

根据上面讲的方法，我们关键是要维护一个入度为 0 的顶点的列表. 代码实现思路如下:

1. 每次在入度为0的列表中取顶点, 取出一个顶点v, 便输出v
2. 然后将所有v指向的顶点的入度减1，并将入度减为0的顶点加入列表
3. 重复步骤1和2
4. 如果最终输出的顶点数量小于总顶点数量, 说明有环

取顶点的顺序不同会得到不同的拓扑排序序列，当然前提是该图存在多个拓扑排序序列。代码在上面有了, 其中的topologic_sort便是, 我们尝试用此代码来测试了如下DAG图：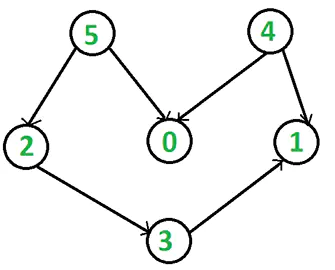

输出结果是 4, 5, 2, 0, 3, 1。这是该图的拓扑排序序列之一。

单调栈

参考

定义：栈内元素保持有序的状态的栈称为单调栈，如下图所示：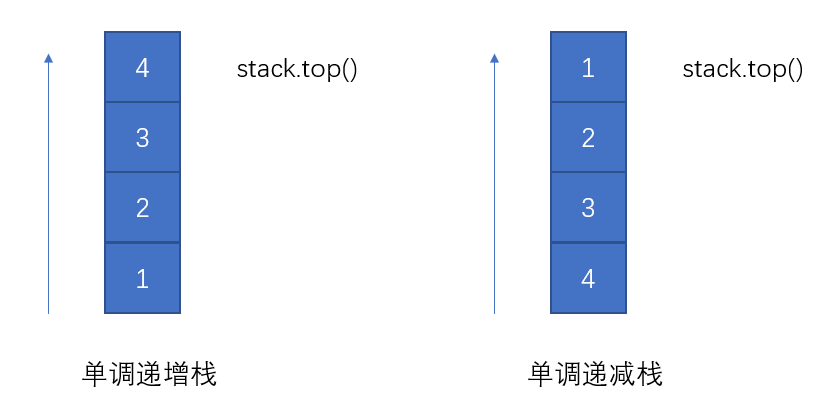

单调栈主要应用：在一个一维数组中，帮助我们找到某个元素的左侧或右侧第一个大于或小于该元素的数。

而所谓 单调栈 则是在栈的 先进后出 基础之上额外添加一个特性：从栈顶到栈底的元素是严格递增（or递减）。具体进栈过程如下：

• 对于单调递减栈，若当前进栈元素为 e，从栈顶开始遍历元素，把小于 e 或者等于 e 的元素弹出栈，直接遇到一个大于 e 的元素或者栈为空为止，然后再把 e 压入栈中。
• 对于单调递增栈，则每次弹出的是大于 e 或者等于 e 的元素。

以 单调递减栈 为例进行说明, 现在有一组数 3，4，2，6，4，5，2，3, 让它们从左到右依次入栈。具体过程如下：

第i步	操作	结果(栈底->栈顶)
1	3进	3
2	3出, 4进	4
3	2进	4 2
4	4 2出, 6进	6
5	4进	6 4
6	4出, 5进	6 5
7	2进	6 5 2
8	2出, 3进	6 5 3

队列中数帽子问题

现有一条排好的队伍，从队首到队尾，队员们都戴着帽子，身高是无序的。假设每个人能看到队伍中在他前面的比他个子矮的人的帽子，（如果出现一个比这个人个子高的人挡住视线，那么此人不能看到高个子前面的任何人的帽子。）现在请计算出这个队伍中一共可以看到多少个帽子？例如给定数组为：[2,1,5,6,2,3]（顺序为从队尾到队首）。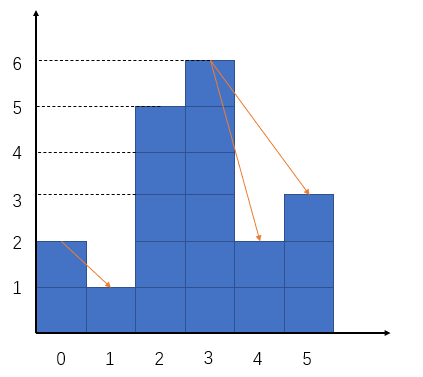

如图示，答案为3。从暴力角度尝试去解这道题，显然可以做到。对于数组中每个元素，向右去找所有比它小的元素（找第第一个比它大的元素），这样总的时间复杂度为O(n^2)，最坏情况是这是一个单调递减数组，每次都要向右找到数组的最末尾。显然这不是理想的解法，我们可以应用单调栈来解决这个问题。其代码如下：

int countHats(vector<int>& heights) {
    heights.push_back(INT_MAX);
    stack<int> stk;
    int sum = 0;
    for(int i=0; i<heights.size(); i++) {
        while( !stk.empty() && heights[i] > heights[stk.top()]) ) {
            int top = stk.top();
            stk.pop();
            sum += i – top – 1;
        }
        stk.push(i);
    }
    return sum;
}

在以上代码中，我们维护了一个单调递减栈，在栈中的元素都是单调递减的，这表明栈内的元素还可能看到比它更小的元素（帽子）。当遇到一个比栈顶元素大的元素时，说明栈顶元素不可能看到比它更小的元素了（因为遮挡作用），这时将栈顶元素pop出来，同时更新sum的值，sum += i – top – 1，表示栈顶元素与这个新元素间的距离，也就是栈顶元素能看到的最多的帽子数。在for循环中，每个元素都会入栈和出栈，在出栈过程中总会计算出栈顶元素能看到的最多的帽子数，并更新sum值，当整个队列循环结束后，得到的sum值就是最后队伍中能看到的帽子总数。注意为了使所有元素都能出栈，（糟糕情况是单调递减数列，这时似乎一次出栈都没有发生，原因是最后一个元素后面不可能有新的元素出现了，但单调栈还在期待新的元素出现，为了反映元素不再出现这一事实，我们假设最后一个元素后面出现了一个无穷大的元素），即heights.push_back(INT_MAX)。

寻找第一个比自己大的数

给一个数组，返回一个大小相同的数组。返回的数组的第i个位置的值应当是，对于原数组中的第i个元素，至少往右走多少步，才能遇到一个比自己大的元素（如果之后没有比自己大的元素，或者已经是最后一个元素，则在返回数组的对应位置放上-1）。
例如给定数组为：[2,1,5,6,2,3]
返回数组应该为：[2,1,1,-1,1,-1]
其实这个问题本质上和数帽子问题是一样的，本质都是找到元素右边第一个比它大的数，代码稍作改动即可。

int countSteps(vector<int>& heights) {
    stack<int> stk;
    vector<int> results(heights.size(), -1);
    for(int i=0; i<heights.size(); i++) {
        while( !stk.empty() && heights[i] > heights[stk.top()]) ) {
            results[stk.top()] = i – stk.top();
            stk.pop();
        }
        stk.push(i);
    }
    return results;
}

接雨水-经典单调栈题

lc42, hard
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。
示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。
示例 2：
输入：height = [4,2,0,3,2,5]
输出：9

参考
理解题目，参考图解，注意题目的性质，当后面的柱子高度比前面的低时，是无法接雨水的
当找到一根比前面高的柱子，就可以计算接到的雨水, 所以使用单调递减栈

对更低的柱子入栈:

• 更低的柱子以为这后面如果能找到高柱子，这里就能接到雨水，所以入栈把它保存起来
• 平地相当于高度 0 的柱子，没有什么特别影响

当出现高于栈顶的柱子时:

• 说明可以对前面的柱子结算了
• 计算已经到手的雨水，然后出栈前面更低的柱子

计算雨水的时候需要注意的是:

• 雨水区域的右边 r 指的自然是当前索引 i
• 底部是栈顶 st.top() ，因为遇到了更高的右边，所以它即将出栈，使用 cur 来记录它，并让它出栈
• 左边 l 就是新的栈顶 st.top()
• 雨水的区域全部确定了，水坑的高度就是左右两边更低的一边减去底部，宽度是在左右中间
• 使用乘法即可计算面积

class Solution(object):
    def trap(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        rain_sum = 0
        _monotone_stack = []
        for i in range(len(height)):
            while _monotone_stack and height[i] > height[_monotone_stack[-1]]:
                cur = _monotone_stack.pop(-1)
                if not _monotone_stack:
                    break
                r = i
                l = _monotone_stack[-1]
                w = r - l - 1
                h = min(height[l], height[r]) - height[cur]
                rain_sum += w * h
            _monotone_stack.append(i)
        return rain_sum

柱状图中最大矩形问题

lc84
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。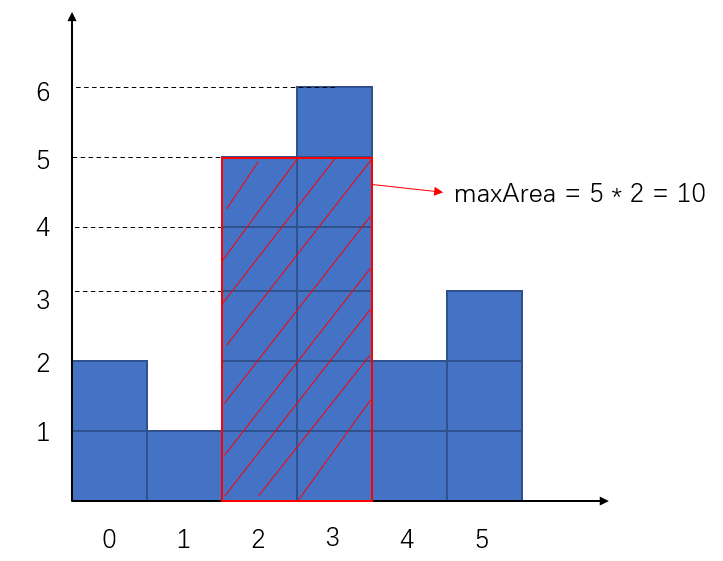

如上图，矩形最大面积为10。这个问题同样可以借助单调栈来解决。在这之前，需要理解如何找到这个最大面积矩形，这个矩形的限制条件有两个，一个是高度（也即组成矩形的最短的那根柱子高度），一个是宽度，（也即组成矩形的柱子个数）。为了找到这个全局最大值，我们遍历所有局部最优情况。那么什么是局部最优解呢，我们将每个柱子的高度作为包含它的矩形的高度，也即这个柱子一定是这个矩形中最低的一个柱子，那么我们下一步是求解这个矩形的宽度，显然我们只需找到这个柱子左边，右边第一个比它低的柱子，就可以求出宽度。这显然让我们想到使用单调栈的数据结构。代码如下：

int largestRectangleArea(vector<int> heights) {
    int maxArea = 0;
    heights.push_back(0);
    stack<int> stk; //monotone stack(ascending)
    for(int i=0; i<heights.size(); i++) {
        while(!stk.empty() && heights[i] < heights[stk.top()]) {
            int top = stk.top();
            stk.pop(); //find the smaller element to the left of the current element
            maxArea = max(maxArea,heights[top]*(stk.empty() ? i : (i - stk.top()-1)));
        }
        stk.push(i);    
    }
    return maxArea;
}

我们维护一个单调递增栈，当遇到一个新元素小于栈顶元素时，发生出栈行为，表示栈顶元素向右遇到了第一个小于它的元素，同时在栈内的栈顶元素的下面一个元素即是栈顶元素向左寻找时第一个小于它的元素。（这一点的原因值得仔细思考，其实是因为栈顶元素与其下面的元素间在原数组中或许存在很多的元素，但它们必然是比栈顶元素大且比栈顶元素下面的元素小的，它们都在之前被弹出了栈。）在出栈行为发生后，我们需要计算以栈顶元素的高度值作为矩形高度时的矩形面积，而矩形宽度已经可以计算了，因为我们找到了栈顶元素左右两侧小于它的第一个元素，于是局部最优解得到计算。在整个循环中，所有元素进栈一次，出栈一次，时间复杂度为O(n)。

并查集

参考

假设有 n 个村庄，有些村庄之间有连接的路，有些村庄之间并没有连接的路

设计一个数据结构，能够快速执行 2 个操作:

• 查询 2 个村庄之间是否有连接的路
• 连接 2 个村庄

使用数组、链表、平衡二叉树、集合 (Set), 查询、连接的时间复杂度都是: O(n), 但是:

• 并查集能够办到查询、连接的均摊时间复杂度都是 O(α(n)), α(n) < 5
• 并查集非常适合解决这类 “连接” 相关的问题

并查集有2个核心操作:

• 查找(Find): 查找元素所在的集合(这里的集合并不是特指Set这种数据结构, 是指广义的数据集合)
• 合并(Union): 将两个元素所在的集合合并为一个集合

假设并查集处理的数据都是整型，那么可以用整型数组来存储数据, 每个数组坐标index表示某个node, 而每个数组元素的值表示node的parent.

初始化时，每个元素各自属于一个单元素集合, 父节点parent都是自己:

举个普通例子, 如果有下图这种情况: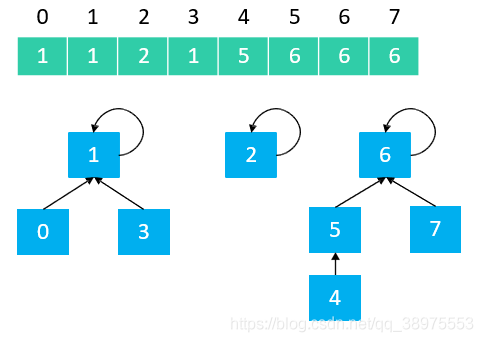

则, 从上图中不难看出:

• 0、1、3 属于同一集合, 这三个node的根节点都是1
• 2 单独属于一个集合, 其根节点是自己也就是2
• 4、5、6、7 属于同一集合, 这四个node的根节点都是6

因此，并查集是可以用数组实现的树形结构 (二叉堆、优先级队列也是可以用数组实现的树形结构)

Find操作

并查集的find查找操作指的是: 通过parent链条不断地向上找，直到找到根节点.
如并查集例子图1, 则

• find(0) == 1
• find(1) == 1
• find(3) == 1
• find(2) == 2
• find(5) == 6
• find(4) == 6
• find(7) == 6

Union操作

Quick Union 的 union(v1, v2)：让 v1 的根节点指向 v2 的根节点

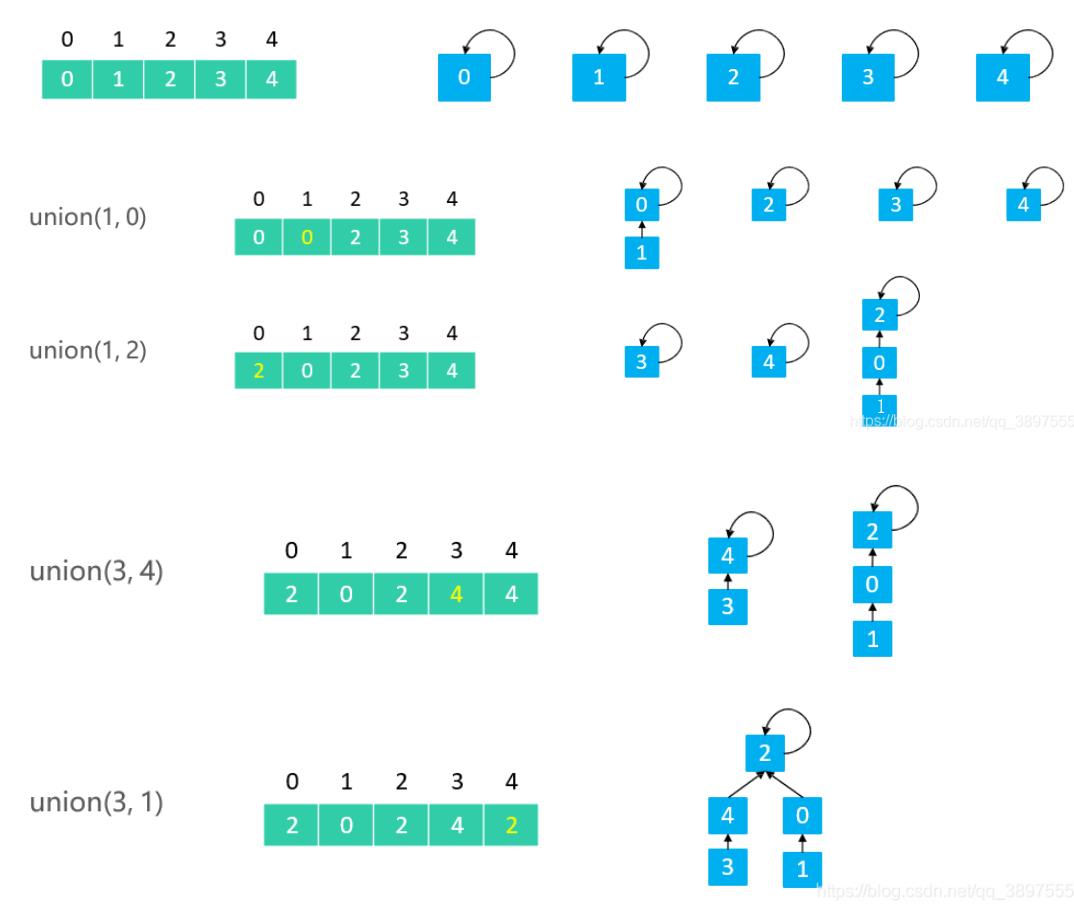
在Union的过程中，可能会出现树不平衡的情况，甚至退化成链表

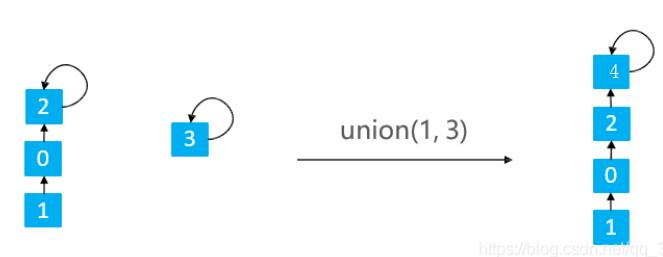
所以一般都会基于rank(也翻译为秩, 其实就是这棵树的层数)的优化, 即层数少的连到层数多的根节点去, 比如下图:

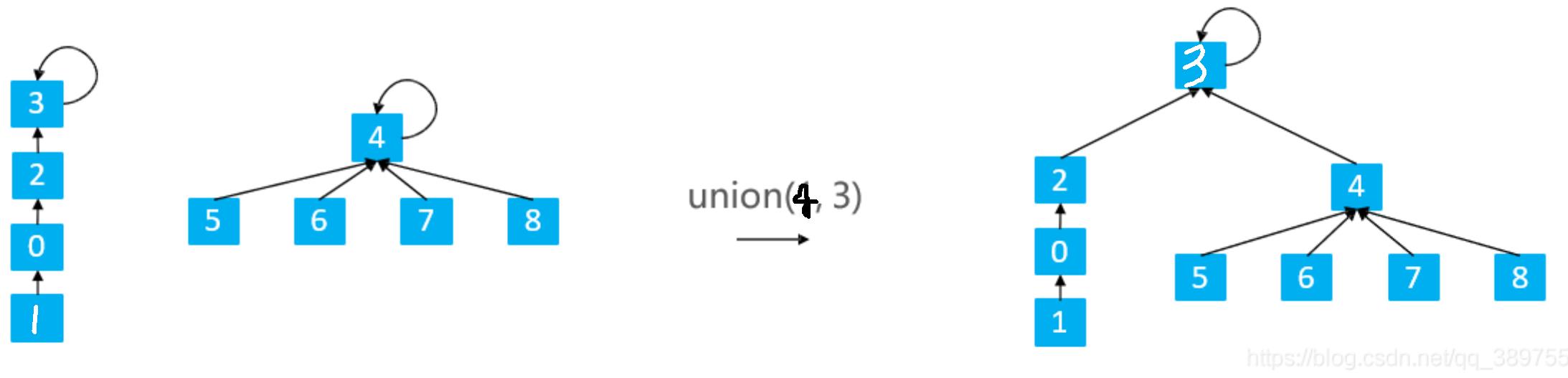
并查集优化-路径压缩

路径减半（Path Halving）：使路径上每隔一个节点就指向其祖父节点(parent的parent), 这是靠在find的时候顺便压缩的

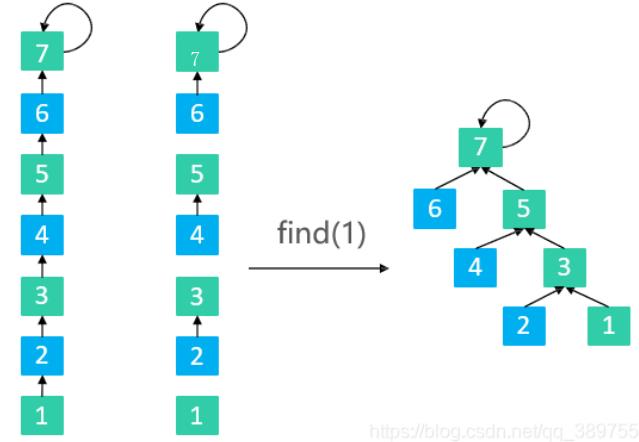
并查集代码实现

class UnionFind:
    def __init__(self, node_count):
        # 初始化时，每个元素各自属于一个单元素集合, 父节点parent都是自己
        self.parent_list = [ i for i in range(node_count) ]
        # 秩都初始化为1, 因为只有自己一个节点的时候, 层数为1
        self.rank_list = [1 for _ in range(node_count) ]
        # 连通分量个数初始化为node个数, 等做union合并操作的时候再减少
        self.connected_component_count = node_count

    # 找到val的根节点
    def find(self, val):
        while(val != self.parent_list[val]):
            # 这一步就是路径压缩了, 路径减半
            self.parent_list[val] = self.parent_list[self.parent_list[val]]
            val = self.parent_list[val]
        return val

    # 把val1所属的集合与val2所属的集合合并, 也就是把val1的根节点指向val2的根节点(或者反之)
    def unite(self, val1, val2):
        # 先找到val1和val2的根节点
        parent1 = self.find(val1)
        parent2 = self.find(val2)
        if parent1 == parent2:
            return
        if self.rank_list[parent1] < self.rank_list[parent2]:
            self.parent_list[parent1] = parent2
        elif self.rank_list[parent1] > self.rank_list[parent2]:
            self.parent_list[parent2] = parent1
        else:  # parent1和parent2的秩相等
            # 这里反过来`self.parent_list[parent1] = parent2`也行
            self.parent_list[parent2] = parent1
            # parent2指向parent1了, 则显而易见的parent2的秩要加1
            self.rank_list[parent2] += 1
        self.connected_component_count -= 1

    def is_connected(self, val1, val2):
        return self.find(val1) == self.find(val2)

并查集实战

岛屿数量和朋友圈数量问题

• 朋友圈问题, lc547, medium
• 岛屿数量问题, lc200, medium

这两题虽然表述不一样但是其实是同一个问题…好奇leetcode为啥没标注为一样
参考

解决本题的思路可以用dfs思路(见本文岛屿数量-经典floodfill问题),
也可以用并查集, 新建一个并查集类 包括parent母结点数组，rank秩数组(优化用)和 count 数量
构造初始化时 需要全图遍历一次 把parent对应的有陆地的标号置为和parent数组下标一样的值。海洋都是-1
比如:

1 1 1 0
0 0 1 1

则 parent = [0,1,2,-1,-1,-1,6,7]
rank为秩 默认为0 若数有2个结点 则秩为1
比如前两个陆地 1 1 合并后 变为 parent = [1,1,2,-1,-1,-1,6,7] 第一块秩为1
count 初始化 遇到陆地就+1 比如 之前的count = 5
正式求解时 再遍历全图 每个点向上下左右四个方向合并 合并一块count--
之前的 会合并4次 count减去4次 就变成1了 只剩1块岛屿
具体见下方cpp代码, 注释写的很详细了

// 定义并查集
class Djset {
private:
    // 数目
    int count;
    // 母结点集合
    vector<int> parent;
    // 秩（优化用）
    vector<int> rank;
public:
	// 初始构造函数 主要初始化3个私有成员
	// 默认parent数值为-1 一维，大小 是grid矩阵行数*列数
	// 默认rank 秩为 0 一维，大小 是grid矩阵行数*列数
	// 默认count数量为0
    Djset(vector<vector<char>>& grid):
        count(0), parent(vector<int>((grid.size()) * (grid[0].size()),-1)),
        rank(vector<int>((grid.size()) * (grid[0].size()), 0))
    {
        int row = grid.size();
        int col = grid[0].size();
        for(int i=0; i<row; ++i){
            for(int j=0; j<col; ++j){
                if(grid[i][j]=='1'){
// 初始化 若有陆地块 则母结点等于自己 否则是默认值-1
// 因为是二维 所以映射到一维数组需要转换一下关系
// : 行号*行数 + 列号                    
                    parent[i*col+j] = i*col+j;

// 遇到一块陆地就+1 后面根据连通分量再删
// 这个count 不是最终答案                    
                    count++;
                }
            }
        }
    }
	// 查 (找结点所在树的根节点) 如1->2->3->5  find(1) 得到 5
    int find(int x){
        // if(x!=parent[x]){
        // （1）路径压缩 优化
        // 所有子结点全部指向根节点 减少树的深度 但开销较大 不推荐
        //     parent[x] = find(parent[x]);
        // }
        // return parent[x];

        // （2）路径减半 优化
		// 使路径上每隔一个节点就指向其祖父节点(parent的parent)
		// 以 1->2->3->4->5 为例  若find(1) 路径查找优化为
		// 1->3->5 路径减半 减少树的深度 
        while(x!=parent[x]){
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
	// 并 (一个结点树并到另一个结点树上)
    void unite(int x1, int x2){
		// 使用秩优化 按秩合并 避免合成后变成单链表 O(n)复杂度
		// 找到 x1 和 x2两个树的根结点
        int f1 = find(x1);
        int f2 = find(x2);
		// 不相等才合并 相等就不需要合并了 证明在一棵树上
        if(f1!=f2){
		    // 秩f1>f2 f1长一些 把f2的树并在f1上 秩不增加 树总深度不变深
            if(rank[f1]>rank[f2]){
                parent[f2] = f1;  // 理解为 f2->f1
            }else{
		        // 秩f1<=f2 把f1的树并在f2上
                parent[f1] = f2;  // f1->f2
		        // 若 秩f1=f2 合并后秩会+1
		        // 例： f1:1->2  f2:3<-4   合： 1->2->3<-4 
                if(rank[f1]==rank[f2]){
                    rank[f2]++ ;
                }
            }
		    // 两块陆地合并成一块 减去一个数量 很重要！
            count--;
        }
    }
    int get_count() const{
        return count;
    }
};

class Solution {
public:
    int numIslands(vector<vector<char>>& grid) {
        int row = grid.size();
        if(!row){return 0;}
        int col = grid[0].size();
        // 初始化并查集对象
        Djset djs(grid);
        // 全图遍历
        for(int i=0; i<row; ++i){
            for(int j=0; j<col; ++j){
                // 当前块为陆地
                if(grid[i][j]=='1'){
                    // 遍历过 避免重复
                    grid[i][j]='2';
                    // 向四个方向合并 有合并就会减去陆地数目得到最终的数目
                    // 向上
                    if(i-1>=0 && grid[i-1][j]=='1'){
                        djs.unite(i*col+j, (i-1)*col + j);
                    }
                    // 向左
                    if(j-1>=0 && grid[i][j-1]=='1'){
                        djs.unite(i*col+j, (i)*col + j-1);
                    }
                    // 向下
                    if(i+1<row && grid[i+1][j]=='1'){
                        djs.unite(i*col+j, (i+1)*col + j);
                    }
                    // 向右
                    if(j+1<col && grid[i][j+1]=='1'){
                        djs.unite(i*col+j, (i)*col + j+1);
                    }
                }
            }
        }
        // 得到最终数量
        return djs.get_count();       
    }
};

等式方程的可满足性

lc990, medium
给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一：”a==b” 或 “a!=b”。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。
只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。
示例 1：
输入：[“a==b”,”b!=a”]
输出：false
解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。
示例 2：
输入：[“b==a”,”a==b”]
输出：true
解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。
示例 3：
输入：[“a==b”,”b==c”,”a==c”]
输出：true
示例 4：
输入：[“a==b”,”b!=c”,”c==a”]
输出：false
示例 5：
输入：[“c==c”,”b==d”,”x!=z”]
输出：true

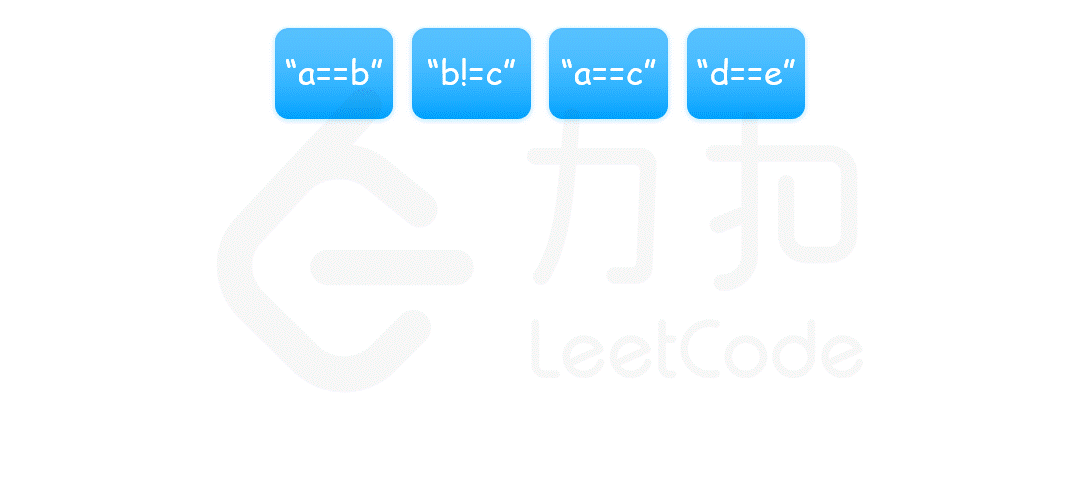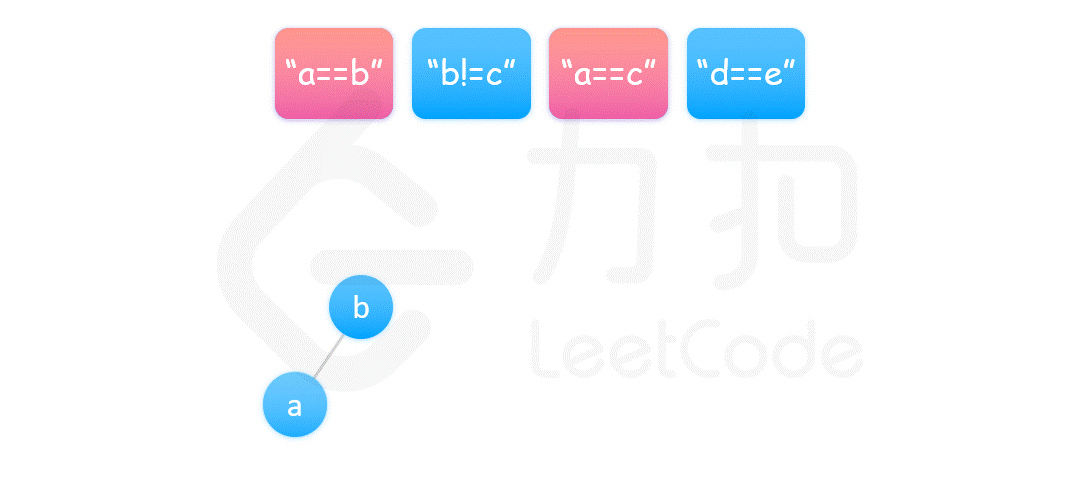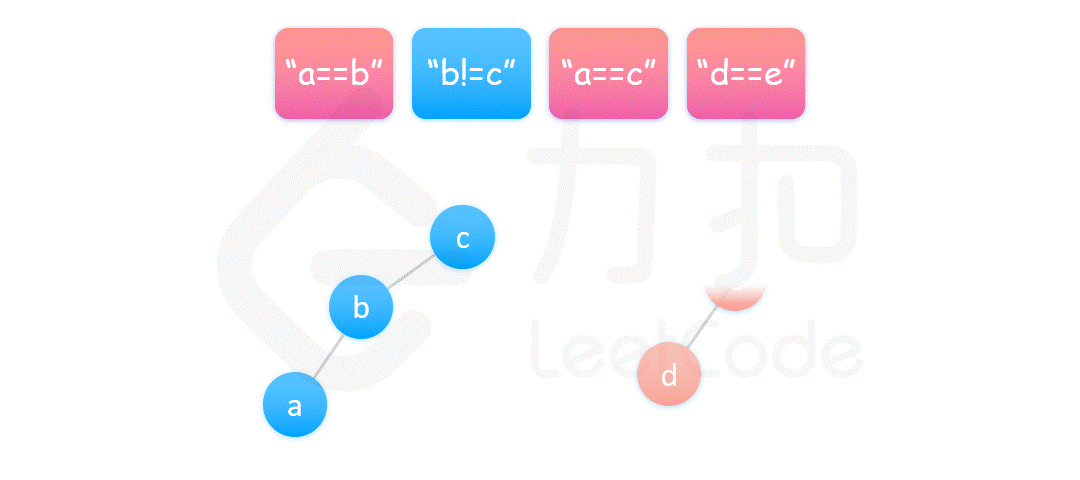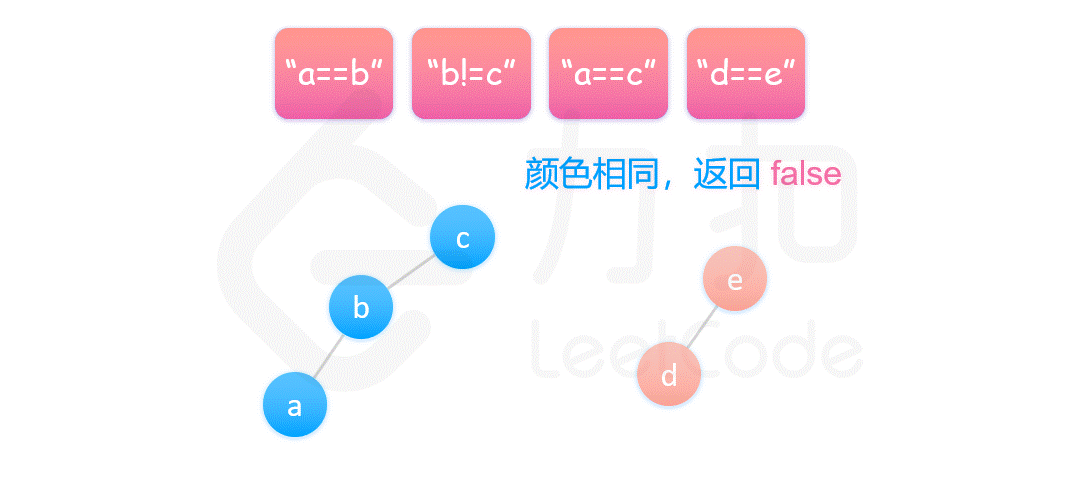
核心思想是，将 equations 中的算式根据 == 和 != 分成两部分，先处理 == 算式，使得他们通过相等关系各自勾结成门派；然后处理 != 算式，检查不等关系是否破坏了相等关系的连通性。

# 26 个英文字母
unionFind = UnionFind(26)
# 先让相等的字母形成连通分量
for equation in equations:
    if equation[1] == '=':
        # ord() 函数它以一个字符作为参数，返回对应的 ASCII 数值
        index1 = ord(equation[0]) - ord('a')
        index2 = ord(equation[3]) - ord('a')
        unionFind.union(index1, index2)

# 检查不等关系是否打破相等关系的连通性
for equation in equations:
    if equation[1] == '!':
        index1 = ord(equation[0]) - ord('a')
        index2 = ord(equation[3]) - ord('a')
        if (unionFind.is_connected(index1, index2)):
            # 如果相等关系成立，就是逻辑冲突
            return False
return True

位运算

位运算的套路技巧

• 异或
  • 异或的性质:
    • 两个数字异或的结果a^b是将 a 和 b 的二进制每一位进行运算，得出的数字。
    • 运算的逻辑是: 如果同一位的数字相同则为 0，不同则为 1
  • 异或的规律:
    • 任何数和本身异或则为0
    • 任何数和 0 异或是本身
    • 任何数和 1 异或 相当与取反
    • 异或运算满足交换律，即: a ^ b ^ c = a ^ c ^ b
  • 异或还可以模拟不算进位的加法:
    12 二进制：1100
    15 二进制：1111
    各位置上的数字分别相加先不管进位的问题, 得到临时二进制结果：
    1100 + 1111 = 0011
    这也可以用1100 ^ 1111 = 0011得到.
    本文算法题不用加减乘除做加法有应用
• 移除最后一个1: a=n&(n-1), 比如n = 0b11010; print bin(n&(n-1)), 则打印0b11000
• 获取最后一个 1: diff=(n&(n-1))^n, 可以看出来是与 移除最后一个1了之后的数做个异或.

python负数存储特殊性

首先python/cpp/java语言中的数字都是以补码形式存储的, 但python没有int/long等不同长度的整形, python编程无需关心整形变量位数.

py的整形数字可以视为是以一个无限长的位存储方式来实现的:

• 比如正数1其实是000000000000000000000000...000000000001, 远不止32位, 而..如果是c++的32位的正数1则只是0x00000001
• 而比如py的负数-1的补码存储则是 111111111111111111111111111...111, 远不止32位, 而..如果是c++的32位的负数-1则只是0xffffffff

但是python:

• Python 中 bin 一个负数（十进制表示），打印输出的却是它的原码的二进制表示加上个负号，方便查看（方便个鬼啊）
• 所以想看python负数的补码得用她和0xffffffff进行与操作, 可以理解为超过32位的东西就不进行考虑了，直接来查看后32位
• 重点: 那如果想从一个负数的补码还原成python的负数, 比如把-3的补码0xfffffffd还原成python的负数, 因为py的整形数字可以视为是以一个无限长的位存储方式来实现的, 所以直接print 0xfffffffd他会打印4294967293, 因为python把0xfffffffd当成了0x000000000fffffffd, 符号位在最前面为0, 当成正数了, 所以我们得对它的后32位之前的所有0都取反变为1, 这样符号位为1才是python存储-1的真正补码形式, 所以对于一个负数res来说, 得这么还原: ~(res ^ 0xffffffff), 要先将 末尾32 位取反（即 res ^ 0xffffffff ），再将所有位取反（即 ~ ). 两个组合操作实质上是将数字 末尾32 以前的位取反， 末尾32 位不变。

a = bin(3)
print(a)
# out: 0b11

# Python 中 bin 一个负数（十进制表示），
# 打印输出的却是它的原码的二进制表示加上个负号，方便查看（方便个鬼啊）
a = bin(-3)
print(a)
# out: -0b11
 
# 所以想看python负数的补码得用她和0xffffffff进行与操作,
# 可以理解为超过32位的东西就不进行考虑了，直接来查看后32位
b = bin(-3 & 0xffffffff)
print(b)
# out: 0b11111111111111111111111111111101

b = 0xfffffffd
b = ~(b ^ 0xffffffff)
print(b)
# out: -3

二进制中1的个数

剑指15
请实现一个函数，输入一个整数，输出该数二进制表示中 1 的个数。例如，把 9 表示成二进制是 1001，有 2 位是 1。因此，如果输入 9，则该函数输出 2。
示例 1：
输入：00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。

其实这道题用python来解不是很舒服, 接下来我们用适用于大多数语言的思路来写代码.
因为python的int型是无限长度的, 所以我们假定n位64位, 我们不能用把n右移位的思路, 因为大多数语言对于负数的二进制表达都是补码其符号位是1(python的负数表达不太一样, -2打印出来表示为-0b10, 但实际上内存中还是以补码来存的, 为11111110, 所以下方代码对于python也是对的), 右移的话, 左边是要补1的, 代码不好写.
因此我们采取用flag=1每次左移一位然后与n做位与运算即可

class Solution_jzo15(object):
    def hammingWeight(self, n):
        """
        :type n: int
        :rtype: int
        """
        # 我们采取用1每次左移一位然后与n做位与运算即可
        _flag = 1
        cnt = 0
        move_cnt = 0
        while _flag:
            if n & _flag:
                cnt += 1
            _flag = _flag << 1
            move_cnt += 1
            if move_cnt >= 64:
                # 因为python的int型是无限长度的...
                # 所以要用64次限制一下..
                break
        return cnt

不用加减乘除做加法

剑指65
写一个函数，求两个整数之和，要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。
示例:
输入: a = 1, b = 1
输出: 2

参考
举个例子:
12 二进制为：1100
15 二进制为：1111
各位置上的数字分别相加先不管进位的问题则：1100 + 1111 = 0011
得到临时不管进位的二进制结果temp: 0011(十进制位3), 那不用加法如何模拟? 可以用异或模拟
1100 ^ 1111 = 0011
计算进位的数字, 得到进位结果: 11000(十进制为24), 进位计算如何不用加法模拟?
相与，左移一位则可得到进位结果carry:
(1100 & 1111) << 1 = 11000
然后temp + carry 则为 十进制的3+24=27, 用上述的方法再算一次temp + carry
则cpp代码如下:

class Solution {
public:
    int add(int a, int b) {
        while (b) {
            // LeetCode c++ 不允许负数左移操作，所以要转换成无符号整数
            // 当然面试的时候不需要转换哈
            int carry = (unsigned int)(a & b) << 1;
            a ^= b;
            b = carry;
        }
        return a;
    }
};

因为python负数存储特殊性, 需要特殊处理一哈, 如下:

class Solution(object):
    def add(self, a, b):
        a &= 0xffffffff
        b &= 0xffffffff
        while b != 0:
            temp = a ^ b
            carry = (a & b) << 1 & 0xffffffff

            a = temp
            b = carry
        # return a if (a & 0xffffffff) >> 31 == 0 else ~(a ^ 0xffffffff)
        if a < 0x80000000:#如果是正数的话直接返回
            return a
        else:
            return  ~(a^0xffffffff)#是负数的话,转化成其原码

只出现一次的数字系列

出现奇数次

题目: 给定一个含有n个元素的整型数组a，其中只有一个元素出现奇数次，找出这个元素。
解决问题的关键是要想明白，按位异或运算满足结合律，偶数个异或结果是0，奇数个异或结果是本身，如1 ^ 2 ^ 3 ^ 1 ^ 2 ^ 3 ^ 3 = (3 ^ 3 ^ 3) ^ (1 ^ 1) ^ (2 ^ 2) = 3^ 0 ^ 0 = 3

只出现一次的数字系列1

lc136
给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        # 我们执行一次全员异或即可
        single_number = 0
        for num in nums:
            single_number ^= num
        return single_number

只出现一次的数字系列2

lc137
给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。
说明：
你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？
示例 1:
输入: [2,2,3,2]
输出: 3
示例 2:
输入: [0,1,0,1,0,1,99]
输出: 99

参考
建立一个长度为 32 的数组 counts ，通过以下方法可记录所有数字的各二进制位的 1 的出现次数。
将 counts 各元素对 3 求余，则结果为 “只出现一次的数字” 的各二进制位。
利用 左移操作 和 或运算 ，可将 counts 数组中各二进位的值恢复到数字 res 上
最终返回 res 即可。
实际上，只需要修改求余数值 m ，即可实现解决 除了一个数字以外，其余数字都出现 m 次 的通用问题.

class Solution_lc137(object):
    def singleNumber(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        counts = [ 0 for _ in range(32) ]
        # 建立一个长度为 32 的数组 counts ，通过以上方法可记录所有数字的各二进制位的 1 的出现次数。
        for cur_num in nums:
            _flag = 1
            for j in range(32):
                if cur_num & _flag:
                    counts[j] += 1
                _flag = _flag << 1
        res = 0
        m = 3
        # 将 counts 各元素对 3 求余，则结果为 “只出现一次的数字” 的各二进制位。
        # 利用 左移操作 和 或运算 ，可将 counts 数组中各二进位的值恢复到数字 res 上
        # 最终返回 res 即可。
        # 实际上，只需要修改求余数值 m ，即可实现解决 除了一个数字以外，
        # 其余数字都出现 m 次 的通用问题.
        for i in range(32):
            res <<= 1
            res |= counts[31-i] % m
        # 那如果想从一个负数的补码还原成python的负数, 
        # 比如把`-3`的补码`0xfffffffd`还原成python的负数,
        #  因为py的整形数字可以视为是以一个无限长的位存储方式来实现的,
        #   所以直接`print 0xfffffffd`他会打印`4294967293`,
        #    因为python把`0xfffffffd`当成了`0x000000000fffffffd`, 
        #    符号位在最前面为0, 当成正数了, 所以我们得对它的后32位之前的所有0都取反变为1,
        #     这样符号位为1才是python存储`-1`的真正补码形式,
        # 	 所以对于一个负数`res`来说, 得这么还原: `~(res ^ 0xffffffff)`, 
        # 	 要先将 末尾32 位取反（即 res ^ 0xffffffff ），再将所有位取反（即 ~ ).
        # 	  两个组合操作实质上是将数字 末尾32 以前的位取反， 末尾32 位不变。
        return res if (counts[31] % m) == 0 else ~(res ^ 0xffffffff)

只出现一次的数字系列3

lc260
给定一个整数数组 nums，其中恰好有两个元素只出现一次，其余所有元素均出现两次。 找出只出现一次的那两个元素。
示例 :
输入: [1,2,1,3,2,5]
输出: [3,5]
注意：
结果输出的顺序并不重要，对于上面的例子， [5, 3] 也是正确答案。
你的算法应该具有线性时间复杂度。你能否仅使用常数空间复杂度来实现？

参考
现在数组中有两个数字只出现1次，直接异或一次只能得到这两个数字的异或结果，但光从这个结果肯定无法得到这个两个数字。因此基于single number I 的思路——数组只能有一个数字出现1次。

设题目中这两个只出现1次的数字分别为A和B，如果能将A，B分开到二个数组中，那显然符合“异或”解法的关键点了。

因此这个题目的关键点就是将A，B分开到二个数组中。由于A，B肯定是不相等的，因此在二进制上必定有一位是不同的。根据这一位是0还是1可以将A，B分开到A组和B组。而这个数组中其它数字要么就属于A组，要么就属于B组。再对A组和B组分别执行“异或”解法就可以得到A，B了。而要判断A，B在哪一位上不相同，只要根据A异或B的结果就可以知道了，这个结果在二进制上为1的位就说明A，B在这一位上是不相同的。

比如 int a[] = {1, 1, 3, 5, 2, 2}, 整个数组异或的结果为3^5，即 0b0011 ^ 0b0101 = 0b0110, 而
0b0110则表示3和5这两个数在第1位和第2位不同。我们取第1位来分组(当然取第2位来分组也可以), 因此整个数组根据这一位是0还是1分成两组。

a[0] =1  0b0001  第一组
a[1] =1  0b0001  第一组
a[2] =3  0b0011  第二组
a[3] =5  0b0101  第一组
a[4] =2  0b0010  第二组
a[5] =2  0b0010  第二组

第一组有{1,1,5}，第二组有{3,2,2}，然后对这二组分别执行“异或”解法就可以得到5和3了。 代码如下:

def singleNumber(self, nums: List[int]) -> List[int]:
    ret = 0  # 所有数字异或的结果
    a = 0
    b = 0
    for n in nums:
        ret ^= n
    # 找到第一位不是0的
    h = 1
    while(ret & h == 0):
        h <<= 1
    for n in nums:
        # 根据该位是否为0将其分为两组
        if (h & n == 0):
            a ^= n
        else:
            b ^= n
    return [a, b]

排序算法

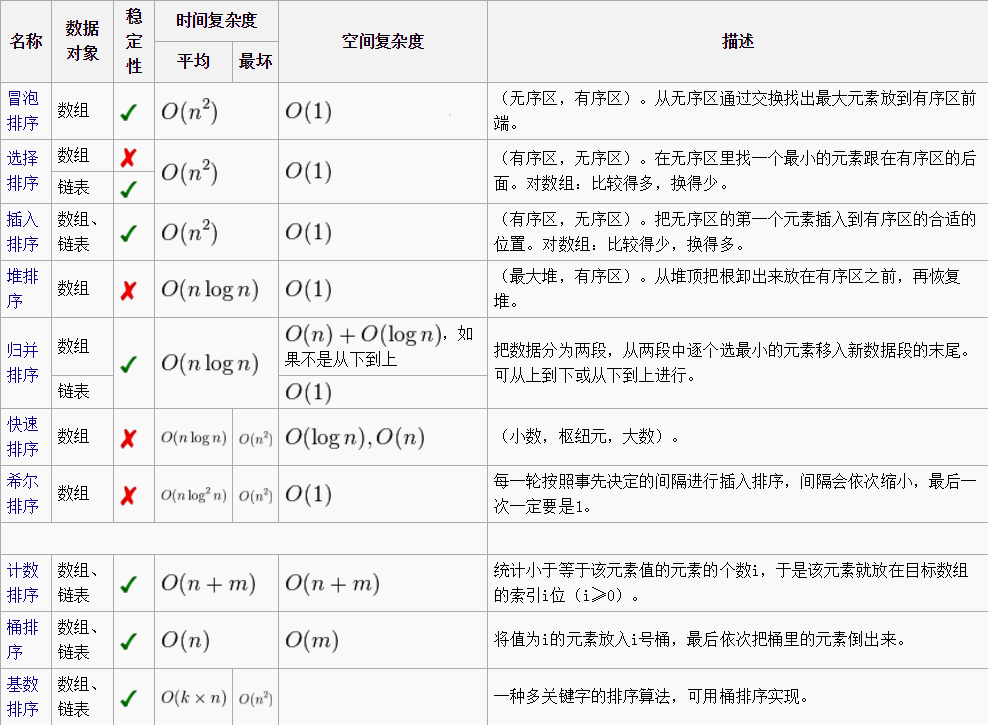
各类排序总览

• 比较交换类排序:
  • 堆排序
  • 快排
  • 插排
  • 冒泡排序
  • 选择排序
  • 希尔排序
• 桶思想类排序:
  • 基数排序：根据键值的每位数字来分配桶；
  • 计数排序：每个桶只存储单一键值；
  • 桶排序：每个桶存储一定范围的数值；

不常用算法一览

冒泡排序

每一轮循环都会有一个最大的数慢慢移动到最后, 很像是冒出一个泡泡, 因而得名.
算法步骤:

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

void bubble_sort(int* arr, int arr_len){
  for(int i = 0; i < arr_len; ++i){
    for(int j = i+1; j < arr_len; ++j){
      if(arr[i] > arr[j]){
        auto temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
      }
    }
  }
}

选择排序

首先在未排序序列中找到最小（大）元素，然后选择它存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小（大）元素，然后选择它放到已排序序列的末尾。
重复第二步，直到所有元素均排序完毕。

void select_sort(int arr[], int arr_len){
  for(int i = 0; i < arr_len; ++i){
    auto cur_min_index = i;
    for(int j = i + 1; j < arr_len; ++j){
      if(arr[cur_min_index] > arr[j]){
        cur_min_index = j;
      }
    }
    auto temp = arr[i];
    arr[i] = arr[cur_min_index];
    arr[cur_min_index] = temp;
  }
}

希尔排序

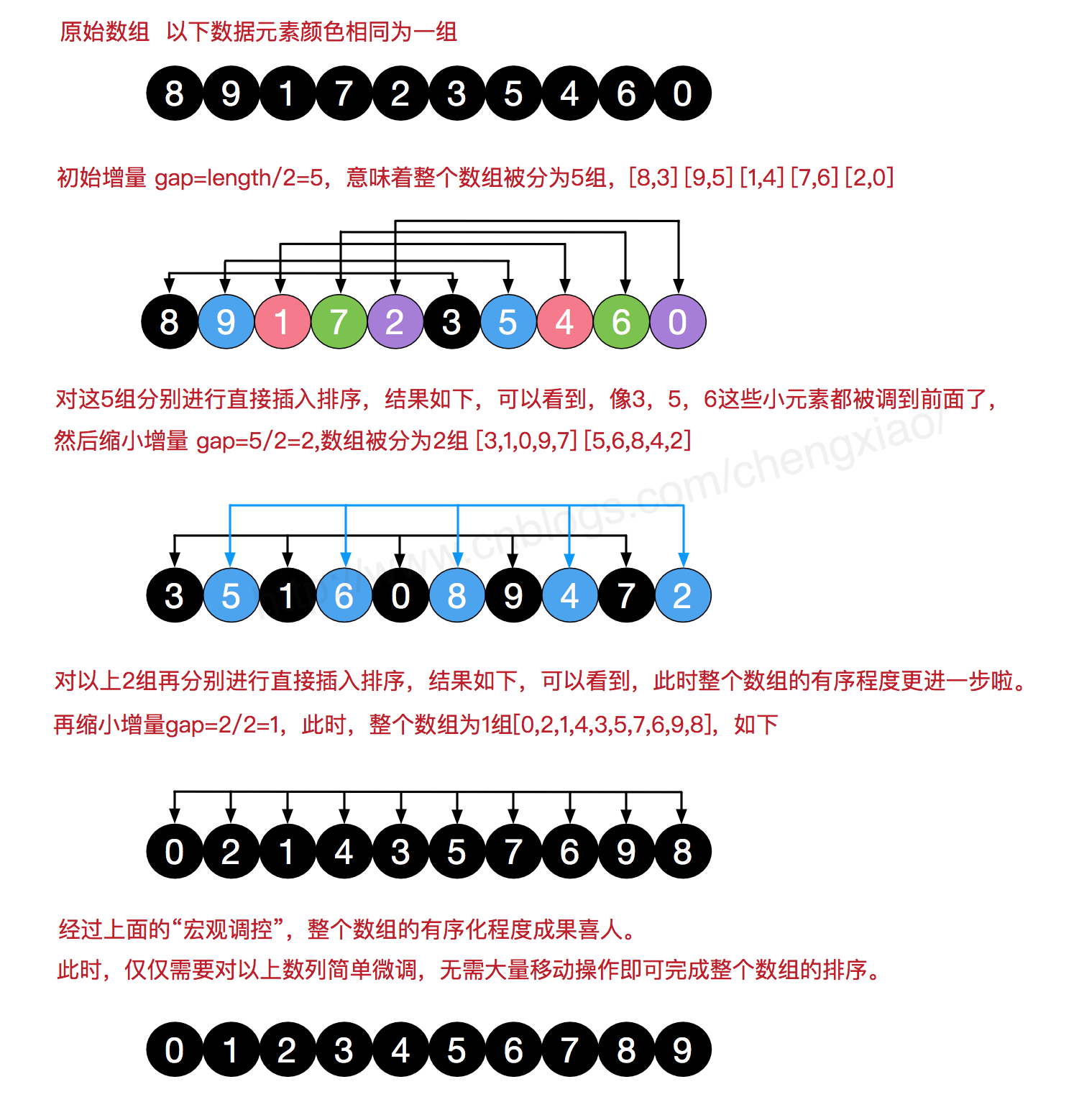
希尔排序(Shell Sort)是插入排序的一种算法，是对直接插入排序的一个优化，也称缩小增量排序。希尔排序是非稳定排序算法。希尔排序因DL．Shell于1959年提出而得名。

简单插入排序很循规蹈矩，不管数组分布是怎么样的，依然一步一步的对元素进行比较，移动，插入，比如[5,4,3,2,1,0]这种倒序序列，数组末端的0要回到首位置很是费劲，比较和移动元素均需n-1次。

而希尔排序在数组中采用跳跃式分组的策略，通过某个增量将数组元素划分为若干组，然后分组进行插入排序，随后逐步缩小增量，继续按组进行插入排序操作，直至增量为1时排完就完毕了。

希尔排序通过这种策略使得整个数组在初始阶段达到从宏观上看基本有序，小的基本在前，大的基本在后。然后缩小增量，到增量为1时，其实多数情况下只需微调即可，不会涉及过多的数据移动, 此时排序完毕了.

计数排序

让我们先来回顾一下经典的排序算法，无论是归并排序，冒泡排序还是快速排序等等，都是基于元素之间的比较来进行排序的。但是有一种特殊的排序算法叫计数排序，这种排序算法不是基于元素比较，而是利用数组下标来确定元素的正确位置。

有这样一道排序题：数组里有20个随机数，取值范围为从0到10，要求用最快的速度把这20个整数从小到大进行排序。请问怎么做?

在这个题目里，随即整数的取值范围是从0到10，那么这些整数的值肯定是在0到10这11个数里面。于是我们可以建立一个长度为11的数组，数组下标从0到10，元素初始值全为0，如下所示：

先假设20个随机整数的值是：9, 3, 5, 4, 9, 1, 2, 7, 8，1，3, 6, 5, 3, 4, 0, 10, 9, 7, 9
让我们先遍历这个无序的随机数组，每一个整数按照其值对号入座，对应数组下标的元素进行加1操作。
比如第一个整数是9，那么数组下标为9的元素加1：

第二个整数是3，那么数组下标为3的元素加1：

继续遍历数列并修改数组……
最终，数列遍历完毕时，数组的状态如下：

数组中的每一个值，代表了数列中对应整数的出现次数。
有了这个统计结果，排序就很简单了，直接遍历数组，输出数组元素的下标值，元素的值是几，就输出几次：
0, 1, 1, 2, 3, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 9, 9, 9, 10
显然，这个输出的数列已经是有序的了。

这就是计数排序的基本过程，它适用于一定范围的整数排序。在取值范围不是很大的情况下，它的性能在某些情况甚至快过那些O(nlogn)的排序，例如快速排序、归并排序。

桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

• 在额外空间充足的情况下，尽量增大桶的数量
• 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

同时，对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

• 什么时候最快: 当输入的数据可以均匀的分配到每一个桶中。
• 什么时候最慢: 当输入的数据被分配到了同一个桶中
  • 如何解决分布不平均的情况: 运用多层桶的思想, 比如游戏排行榜就是一个典型的桶排序适用场景, 针对这些划分之后还是有一些桶区间数量非常多，我们可以继续划分，比如，战力在1到1000之间的玩家比较多，我们就将这个区间继续划分为10个小区间，1到100，101到200，201到300…901到1000。如果划分之后，101到200元之间的还是太多，那就继续再划分

元素分布在桶中：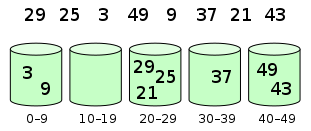

然后，元素在每个桶中排序：

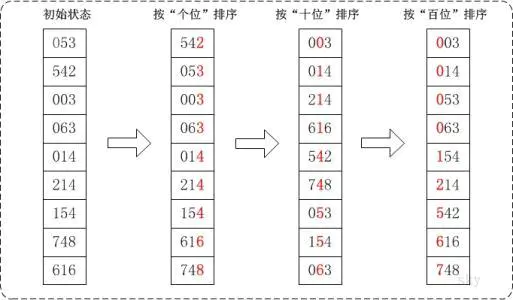
基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

代码如下:

def radix_sort(s):
    i = 0  # 记录当前正在排拿一位,最低位为1
    max_num = max(s)  # 最大值
    j = len(str(max_num))  # 记录最大值的位数
    while i < j:
        bucket_list = [[] for _ in range(10)]  # 初始化桶数组
        for x in s:
            bucket_list[int(x / (10 ** i)) % 10].append(x)  # 找到位置放入桶数组
        print(bucket_list)
        s.clear()
        for x in bucket_list:  # 放回原序列
            for y in x:
                s.append(y)
        i += 1

a = [334, 5, 67, 345, 7, 345345, 99, 4, 23, 78, 45, 1, 3453, 23424]
radix_sort(a)
print('最后的结果是:', a)

'''
[[], [1], [], [23, 3453], [334, 4, 23424], [5, 345, 345345, 45], [], [67, 7], [78], [99]]
[[1, 4, 5, 7], [], [23, 23424], [334], [345, 345345, 45], [3453], [67], [78], [], [99]]
[[1, 4, 5, 7, 23, 45, 67, 78, 99], [], [], [334, 345, 345345], [23424, 3453], [], [], [], [], []]
[[1, 4, 5, 7, 23, 45, 67, 78, 99, 334, 345], [], [], [23424, 3453], [], [345345], [], [], [], []]
[[1, 4, 5, 7, 23, 45, 67, 78, 99, 334, 345, 3453], [], [23424], [], [345345], [], [], [], [], []]
[[1, 4, 5, 7, 23, 45, 67, 78, 99, 334, 345, 3453, 23424], [], [], [345345], [], [], [], [], [], []]
最后的结果是: [1, 4, 5, 7, 23, 45, 67, 78, 99, 334, 345, 3453, 23424, 345345]
'''

实用排序算法要点总结

• 实用的基础排序算法有四种:
  • 插入排序 : 在小数据量或者数据都较为有序的时候比起归并和快速排序有更佳的时间效率, 插入排序在这种情况下，只需要从头到尾扫描一遍，交换、移动少数元素即可；时间复杂度近乎 o(N)))。 所以插入排序经常可以当作是其他排序算法的子过程, 下面代码会有体现
  • 快速排序 : 时间复杂度依赖数据打乱的程度
    • 快排最差情形的时间复杂度是O(n2), 平均是O(nlogn)
    • 就地快速排序使用的空间是O(1)的，也就是个常数级；而真正消耗空间的就是递归调用了，因为每次递归就要保持一些数据；
      • 最优的情况下空间复杂度为：O(logn) ；每一次都平分数组的情况
      • 最差的情况下空间复杂度为：O( n ) ；退化为冒泡排序的情况
    • 选择基准的方式决定了两个分割后两个子序列的长度，进而对整个算法的效率产生决定性影响, 比如当如果一个有序递增序列, 每次选基准都选最后一个, 那肯定效率 很差了啊, 此时最差情形的时间复杂度是O(n2)
    • 不稳定是因为等于pivot的num和pivot交换: 如果一个数num刚好跟pivot相等, 那partition完的时候, pivot要和partition index位置的数做交换, 如果这个数num刚好在partition index这个位置, 那这两个数就会发生交换, 然后肯定就不稳定了啊
      • 举个例子：
        待排序数组: int a[] ={1, 2, 2, 3, 4, 5, 6};
        在快速排序的随机选择比较子(即pivot)阶段：
        若随机选择到了a[2]（即数组中的第二个2）为比较子，，而把大于等于比较子的数均放置在大数数组中，则a[1]（即数组中的第一个2）会到pivot的右边， 那么数组中的两个2非原序（这就是“不稳定”）。
        若随机选择到了a[1]为比较子，而把 小于等于 比较子的数均放置在小数数组中，则数组中的两个2顺序也非原序
        这就说明，quick sort是不稳定的。
  • 归并排序 : 时间复杂度稳定但是占用2N的内存
    • 归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间：n + logn；所以空间复杂度为: O(n)
    • 还有一种空间复杂度为O(1)的归并排序的自底向上的实现, 下文会讲
  • 堆排序: 为什么在平均情况下快速排序比堆排序要优秀?
    堆排序是渐进最优的比较排序算法，达到了O(nlgn)这一下界，而快排有一定的可能性会产生最坏划分，时间复杂度可能为O(n^2)，那为什么快排在实际使用中通常优于堆排序？
    • 虽然quick_sort会n^2（其实有稳定的nlgn的版本, 比如优化版的三路快排），但这毕竟很少出现。heap_sort大多数情况下比较次数都多于quick_sort，尽管大家都是nlogn。那就让倒霉蛋倒霉好了，大多数情况下快才是硬道理。
    • 堆排比较的几乎都不是相邻元素，对cache极不友好，这才是很少被采用的原因。数学上的时间复杂度不代表实际运行时的情况.快排是分而治之，每次都在同一小段进行比较，最后越来约接近局部性。反观堆排，堆化过程中需要一直拿index的当前元素A和处于index*2 + 1 的左子元素B以及处于index*2 + 2 的右子元素C比较, 两个元素距离较远。(局部性原理是指CPU访问存储器时，无论是存取指令还是存取数据，所访问的存储单元都趋于聚集在一个较小的连续区域中。)

• 代码书写技巧:

  • 归并和快排都是当left_index >= right_index时, 停止递归

  • 快排的partition过程分割index和遍历的初始index的选择:

    • 普通快排:

      # partition_index 在还没开始遍历之前时应该指向待遍历元素的最左边的那个元素的前一个位置
      # 在这里这种写法就是 `left_index`
      # 这才符合partition_index的定义:
      #       partition_indexy指向小于pivot的那些元素的最后一个元素,
      #       即 less_than_pivots_last_elem_index
      # 因为还没找到比pivot小的元素之前, 
      # partition_index是不应该指向任何待遍历的元素的
      partition_index = less_than_pivots_last_elem_index = left_index
      
      i = left_index + 1  # 因为pivot_index取left_index了, 则我们从left_index+1开始遍历

    • 三路快排:

      # lt_index 指向小于pivot的那些元素的最右边的一个元素,
      # lt_index 即 less_than_pivots_last_elem_index
      # 因为还没找到比pivot小的元素之前, 
      # lt_index 是不应该指向任何待遍历的元素的, 
      # gt_index 同理, gt_index指向大于pivot的那些元素的最左边的一个元素,
      lt_index = less_than_pivots_last_elem_index = left_index
      gt_index = right_index + 1
      
      i = left_index + 1  # 因为pivot_index取left_index了, 则我们从left_index+1开始遍历

  • 堆排序:
    如果是对数组的[left_index, right_index]来排序, 且数组的首index为0的话, 则:

    • 最后一个非叶子节点的index为left_index + (length/2 - 1)
    • left_child_index = 2 * (pending_heapify_index-left_index) + 1
    • right_child_index = left_child_index + 1
• 是否原址:
  • 原址: 插入排序、堆排序、快速排序
  • 非原址: 归并排序
• 稳定性:
  • 稳定: 插入排序、归并排序
  • 不稳定: 堆排序、快速排序
• 内省排序: std的sort就是用的内省排序. 此算法首先从快速排序开始，当递归深度超过一定深度（深度为排序元素数量的对数值即logN, 快速排序在理想状态下，应当递归约 log n 次。因此，我们可以说，如果递归深度明显大于 log n，快速排序就掉进陷阱了。于是，我们可以将该阈值设置为 log n 的某一倍数，比如 2log n；一旦递归深度超过 2log n，就从快速排序切换到堆排序。）后转为堆排序。采用这个方法，内省排序既能在常规数据集上实现快速排序的高性能，又能在最坏情况下仍保持O(NlogN)的时间复杂度。不难归纳，这样的内省式排序，策略应该如下：
  1. 在数据量足够大的情况使用快速排序；
  2. 在快速排序掉入陷阱时，主动切换到堆排序；
  3. 在快速排序和堆排序已经做到基本有序的情况下，或者数据量较小的情况下，主动切换到插入排序。

插入排序

想象手上有几张牌， 现在你抽了一张牌， 然后需要从手上最右边的牌开始比较，然后插入到相应位置

通过不断的与前面已经排好序的元素比较并交换,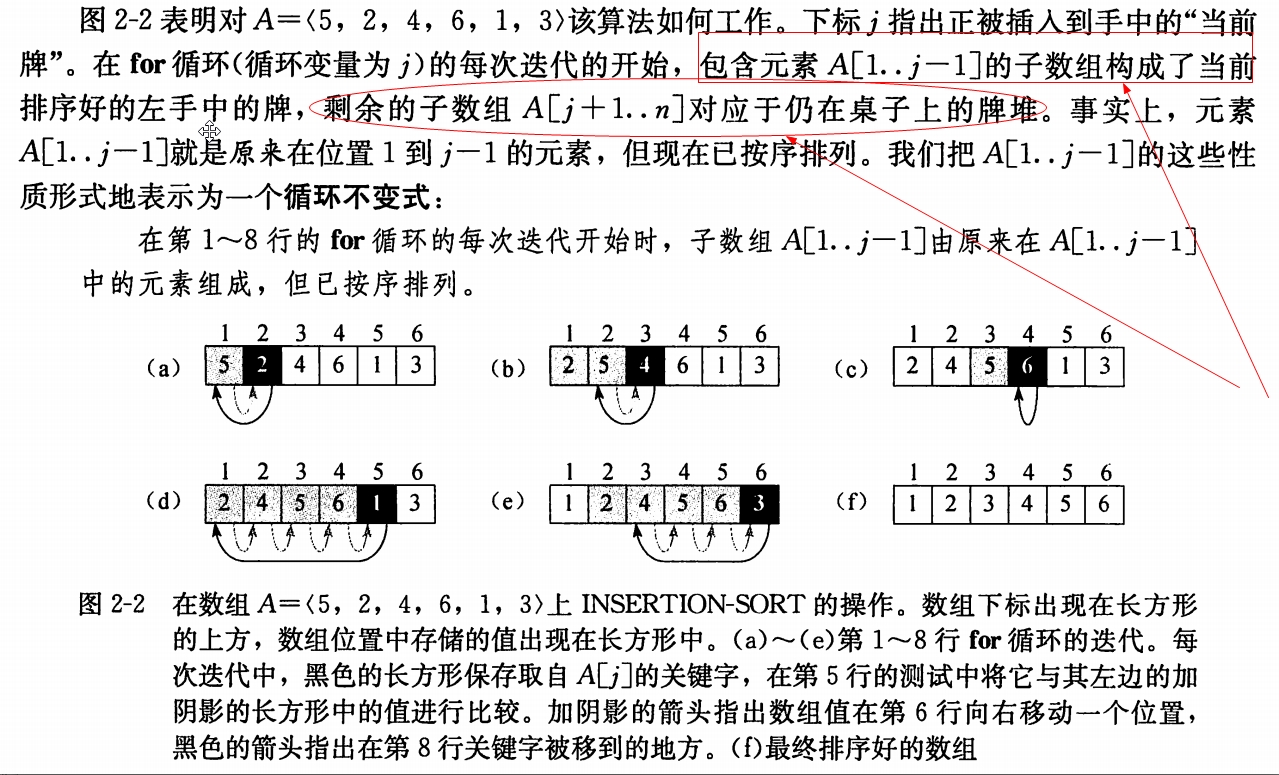

动画演示如下:

python版本

def insert_sort(arr, left_index, right_index):
    if not arr:
        return
    for i in xrange(left_index+1, right_index+1):  # 从left_index+1开始, 也就是从第二个开始
        for j in xrange(i, left_index, -1):
            if arr[j] < arr[j-1]:  # 注意保证j-1大于0
                # 通过不断的与前面已经排好序的元素比较并交换, 
                arr[j-1], arr[j] = arr[j], arr[j-1]
            else:
                break

与

cpp版本

void insert_sort(int* arr, int arr_len){
  for(int i = 1; i < arr_len; ++i){
    for(int j = i; j >= 0; --j){
      if(arr[j] < arr[j-1]){
        swap_elem(arr, j-1, j);
      }
      else{
        break;
      }
    }
  }
}

插排优化

因为基本的插入排序有太多交换操作了, 我们可以用直接赋值来优化

def insert_sort_optimized(arr, left_index, right_index):
    if not arr:
        return
    for i in xrange(left_index+1, right_index+1):  # 从left_index+1开始, 也就是从第二个开始
        temp_i_val = arr[i]
        j = i
        while j >= left_index+1:
            if temp_i_val < arr[j-1]:  # 注意保证j-1大于0
                arr[j] = arr[j-1]  # 通过不断的与前面已经排好序的元素比较并直接赋值
                j -= 1
            else:
                break        
        arr[j] = temp_i_val  # 已经找到该插入的地方了, 直接赋值

归并排序

归并排序用了分治的思想，有很多算法在结构上是递归的：为了解决一个给定的问题，算法要一次或多次地递归调用其自身来解决相关的子问题。这些算法通常采用分治策略（divide-and-conquier）：将原问题划分成n个规模较小而结构与原问题相似的子问题；递归地解决这些子问题，然后再合并其结果，就得到原问题的解。

分治模式在每一层递归上都有三个步骤：

1. 分解（divide）：将原问题分解成一系列子问题；
2. 解决（conquer）：递归地解各子问题。若子问题足够小，则直接求解；
3. 合并：将子问题的结果合并成原问题的解。

归并的具体思路:

回到我们玩扑克牌的例子，假设桌上有两堆牌面朝上的牌，每堆都已排序，最小的牌在顶上。
我们希望把这两堆牌合并成单一的排好序的输出堆，牌面朝下地放在桌上。
我们的基本步骤包括在牌面朝上的两堆牌的顶上两张牌中选取较小的一张，将该牌从其堆中移开（该堆的顶上将
显露一张新牌）并牌面朝下地将该牌放置到输出堆。
重复这个步骤，直到一个输入堆为空，这时，我们只是拿起剩余的输入堆并牌面朝下地将该堆放置到输出堆。

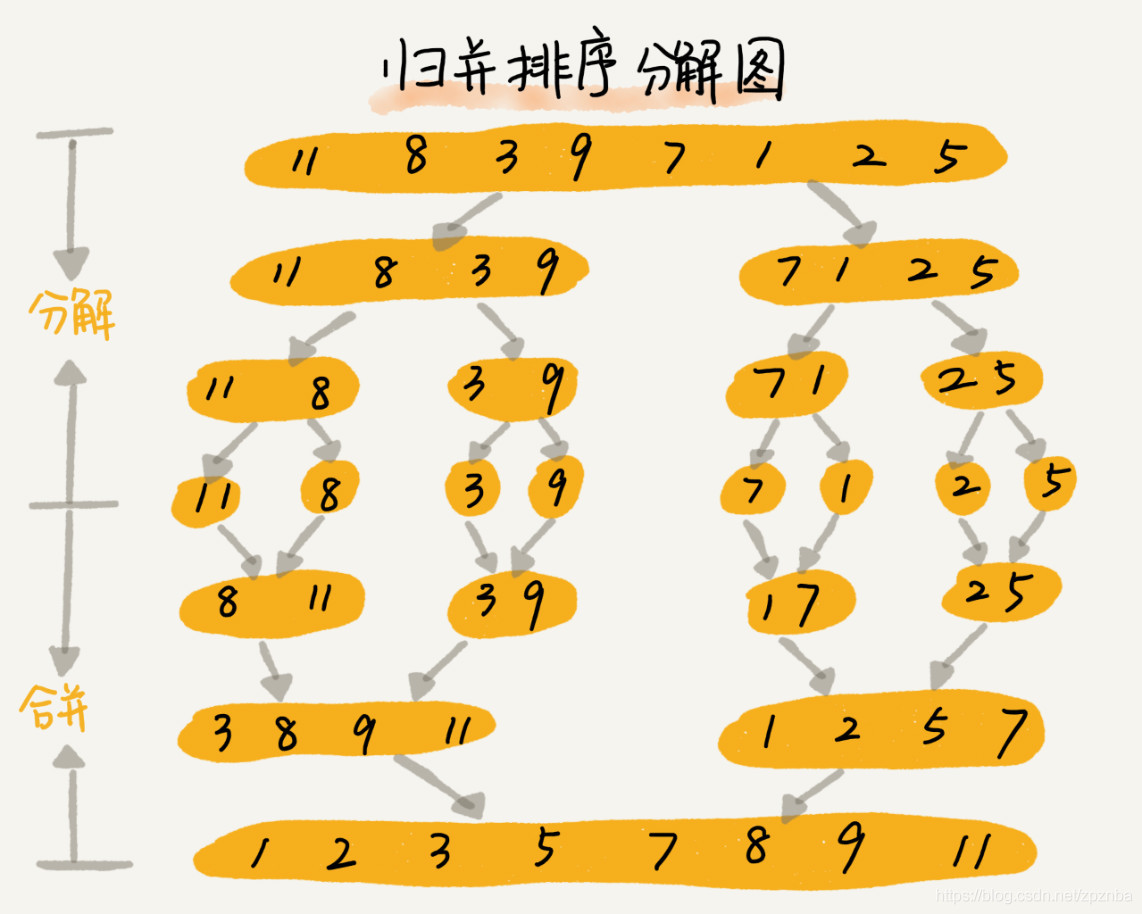
动画演示:

归并排序的merge过程

python版本

def _merge(arr, left_index, mid_index, right_index):
    """
    归并的具体思路:  
        回到我们玩扑克牌的例子，假设桌上有两堆牌面朝上的牌，每堆都已**排序**，最小的牌在顶上。
        我们希望把这两堆牌合并成单一的排好序的输出堆，牌面朝下地放在桌上。
        我们的基本步骤包括在牌面朝上的两堆牌的顶上两张牌中选取较小的一张，将该牌从其堆中移开（该堆的顶上将
        显露一张新牌）并牌面朝下地将该牌放置到输出堆。
        重复这个步骤，直到一个输入堆为空，这时，我们只是拿起剩余的输入堆并牌面朝下地将该堆放置到输出堆。
    """
    # 注释掉下面这句是因为mid不一定等于(l+r)/2, 比如在`merge_sort_bottom_up()`就有可能
    # mid_index = left_index + (right_index - left_index) / 2
    temp_arr = []
    i = left_index
    j = mid_index + 1
    while i <= mid_index and j <= right_index:
        if arr[i] <= arr[j]:
            temp_arr.append(arr[i])
            i += 1
        else:
            temp_arr.append(arr[j])
            j += 1
    # 这一步是模拟: 直到一个输入堆为空，这时，我们只是拿起剩余的输入堆并牌面朝下地将该堆放置到输出堆。
    temp_arr.extend(arr[i:mid_index+1]) 
    temp_arr.extend(arr[j:right_index+1])  # 注意右边界是小于等于right_index的
    # 把归并好的数组数据放到原数组left_index到right_index的位置上去
    for m in xrange(0, right_index-left_index+1):
        arr[left_index+m] = temp_arr[m]

与

cpp版本

void merge(int arr[], int left_i, int mid_i, int right_i){
  std::vector<int> temp_vec = std::vector<int>();
  int i = left_i, j = mid_i + 1;
  while(i <= mid_i && j <= right_i){
    if(arr[i] < arr[j]){
      temp_vec.push_back(arr[i]);
      ++i;
    } else{
      temp_vec.push_back(arr[j]);
      ++j;
    }
  }
  for(; i <= mid_i; ++i)
    temp_vec.push_back(arr[i]);
  for(; j <= right_i; ++j)
    temp_vec.push_back(arr[j]);
  for(int k = left_i; k <= right_i; ++k)
    arr[k] = temp_vec[k-left_i];
}

void merge_sort(int* arr, int left_index, int right_index){
  if(left_index >= right_index){
    return;
  }
  auto mid = left_index + (right_index - left_index) / 2;
  merge_sort(arr, left_index, mid);
  merge_sort(arr, mid+1, right_index);
  if (arr[mid] > arr[mid+1])
    merge(arr, left_index, mid, right_index);
}

归并自顶向下的实现

def merge_sort(arr, left_index, right_index):
    # 当 `merge_sort()` 递归到left_index等于right_index的时候, 
    # 说明left_index, right_index已经相邻了,
    # 说明已经分解到底了, 左右都只剩下一个元素了, 所以此时应该return然后执行 `_merge()` 了
    if not arr or left_index >= right_index:
        return
    # 注意这里不能直接 `mid_index=(left_index+right_index)/2`,
    # 防止当left_index和right_index很大的时候他们之和溢出
    mid_index = left_index + (right_index - left_index) / 2
    merge_sort(arr, left_index, mid_index)
    merge_sort(arr, mid_index+1, right_index)
    _merge(arr, left_index, mid_index, right_index)

归并自顶向下的优化实现

def merge_sort_optimized(arr, left_index, right_index):
    # 当 `merge_sort()` 递归到left_index等于right_index的时候, 
    # 说明left_index, right_index已经相邻了,
    # 说明已经分解到底了, 左右都只剩下一个元素了, 所以此时应该return然后执行 `_merge()` 了
    if not arr or left_index >= right_index:
        return

+    # 优化1:
+    #   数据量较小则使用插入排序
+    if (right_index - left_index) < 15:
+        insert_sort_optimized(arr, left_index, right_index)
+        return

    # 注意这里不能直接 `mid_index=(left_index+right_index)/2`,
    # 防止当left_index和right_index很大的时候他们之和溢出
    mid_index = left_index + (right_index - left_index) / 2
    merge_sort(arr, left_index, mid_index)
    merge_sort(arr, mid_index+1, right_index)

+    # 优化2: 
+    #   因为此时arr[mid_index]是左边的数组里最大的, 而arr[mid_index+1]是右边最小的,
+    #   如果arr[mid_index] <= arr[mid_index+1]则说明这一轮递归的arr的left到right已经是从小到大有序的了
+    #   所以只在对于arr[mid_index] > arr[mid_index+1]的情况,进行merge, 
+    #   对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失(因为多了这行代码判断大小)
+    if arr[mid_index] > arr[mid_index+1]:
        _merge(arr, left_index, mid_index, right_index)

归并自底向上的实现

def merge_sort_bottom_up(arr, left_index, right_index):
    if not arr or left_index >= right_index:
        return
    arr_len = right_index - left_index + 1
    size = 1
    # 注意这里不是 `while size <= arr_len/2`,
    # 否则比如arr_len=12, size为4的话, 只能把[0...7]和[8..11]的这两个区间的元素归并成有序,
    # size=8的话, 大于arr_len/2了,
    # 但只有size为8, 这样2倍size才能把arr全部归并, 所以应该`while size < arr_len`
    while size < arr_len:
        cur_left_index = left_index
        while cur_left_index <= right_index-size:
            cur_mid_index = cur_left_index + size -1
            possible_right_index = cur_left_index + 2*size -1
            # possible_right_index有可能已经大于right_index了, 所以要min一下
            cur_right_index = min(possible_right_index, right_index)
            # 归并从i位置开始的两倍size的一组数据
            _merge(arr, cur_left_index, cur_mid_index, cur_right_index)
            cur_left_index += size * 2  # 每次归并完一组数据就i移动size的两倍
        # print "size: %d" % size
        # print arr
        size *= 2  # size从1开始每次增加两倍

归并自底向上的优化实现

def merge_sort_bottom_up_optimized(arr, left_index, right_index):
    if not arr or left_index >= right_index:
        return

+    # 优化1:
+    #   先以size为16为一组数据来逐个对每组插入排序一遍
+    size = 16
+    cur_left_index = left_index
+    while cur_left_index < right_index:
+        possible_right_index = cur_left_index + 2*size -1
+         # possible_right_index有可能已经大于right_index了, 所以要min一下
+        cur_right_index = min(possible_right_index, right_index)
+        insert_sort(arr, cur_left_index, cur_right_index)
+        cur_left_index += size  # 右移到下一个size大小开头位置
    
    arr_len = right_index - left_index + 1
-   size = 1
    # 注意这里不是 `while size <= arr_len/2`,
    # 比如arr_len=12, size为4的话, 只能把[0, 7]和[8, 11]的两个子数组归并成有序
    # 那只有size为8, 这样2倍size才能把arr全部归并
    # 但size=8的话, 大于arr_len/2了, 所以应该`while size < arr_len`
    while size < arr_len:
        cur_left_index = left_index
        while cur_left_index <= right_index-size:
            cur_mid_index = cur_left_index + size -1
            possible_right_index = cur_left_index + 2*size -1
            # possible_right_index有可能已经大于right_index了, 所以要min一下
            cur_right_index = min(possible_right_index, right_index)
            # 归并从i位置开始的两倍size的一组数据
+           # 优化2: 
+           #   因为此时arr[mid_index]左边的数组里最大的, 而arr[mid_index+1]是右边最小的,
+           #   如果arr[mid_index] <= arr[mid_index+1]则说明这一轮递归的arr的left到right已经是从小到大有序的了
+           #   所以只在对于arr[mid_index] > arr[mid_index+1]的情况,进行merge, 
+           #   对于近乎有序的数组非常有效,但是对于一般情况,有一定的性能损失(因为多了这行代码判断大小)
+           if arr[cur_mid_index] > arr[cur_mid_index+1]:
                _merge(arr, cur_left_index, cur_mid_index, cur_right_index)
            cur_left_index += size * 2  # 每次归并完一组数据就i移动size的两倍
        # print "size: %d" % size
        # print arr
        size *= 2  # size从1开始每次增加两倍

快速排序

与归并排序一样， 快排也是用了分治的思想。

特别注意 : 快排的核心模块是Partition, 而Partition的复杂度为O(N).

你可以想象一个两副牌然后随意取出一张牌pivot，其他的所有牌都跟这张pivot牌比较，

大的放右边那一摞A，小的放左边B。
接着再从左边这一摞B再随意取出一张牌pivot，其他的所有牌都跟这张pivot牌比较，

大的放右边那一摞，小的放左边，递归下去。
A也重复上述步骤递归。

递归结束之后， 左边的都比右边的小， 而且是有序的。

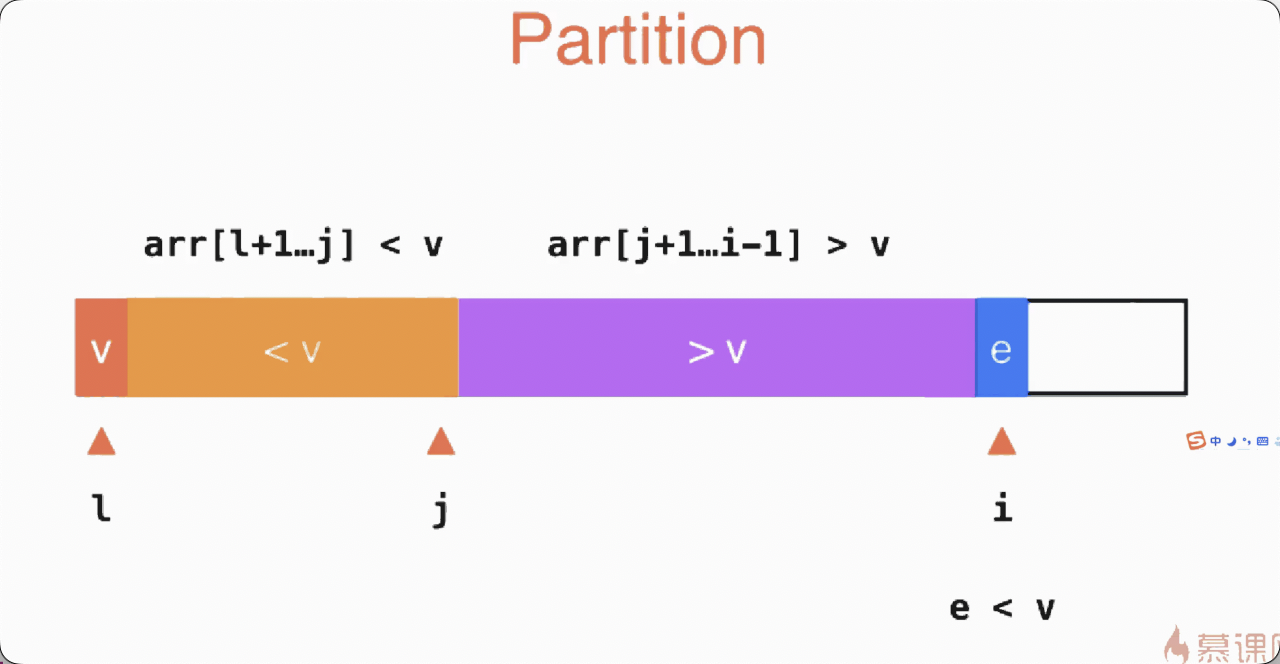
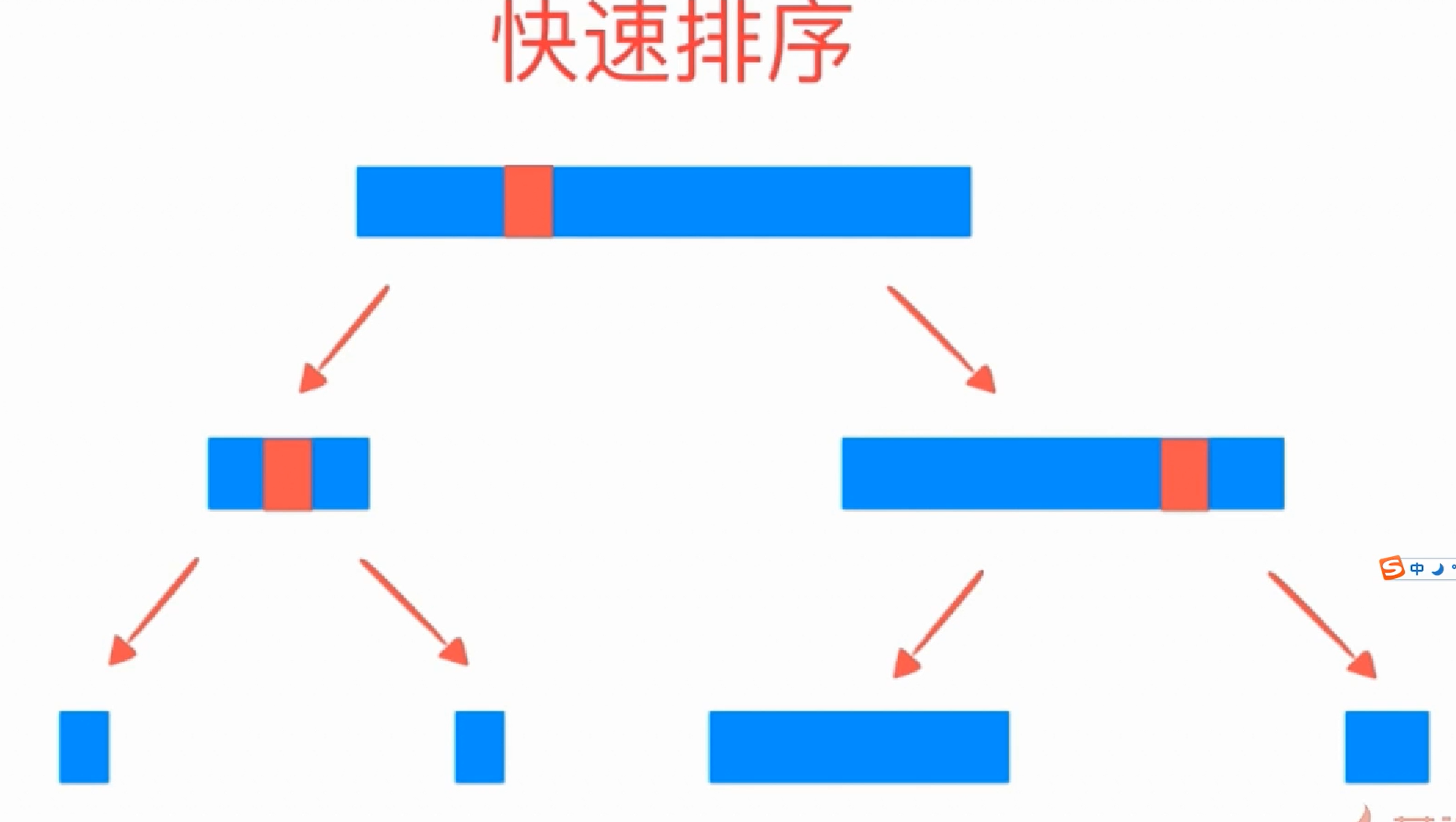
动画演示:

快排效率很差的情况

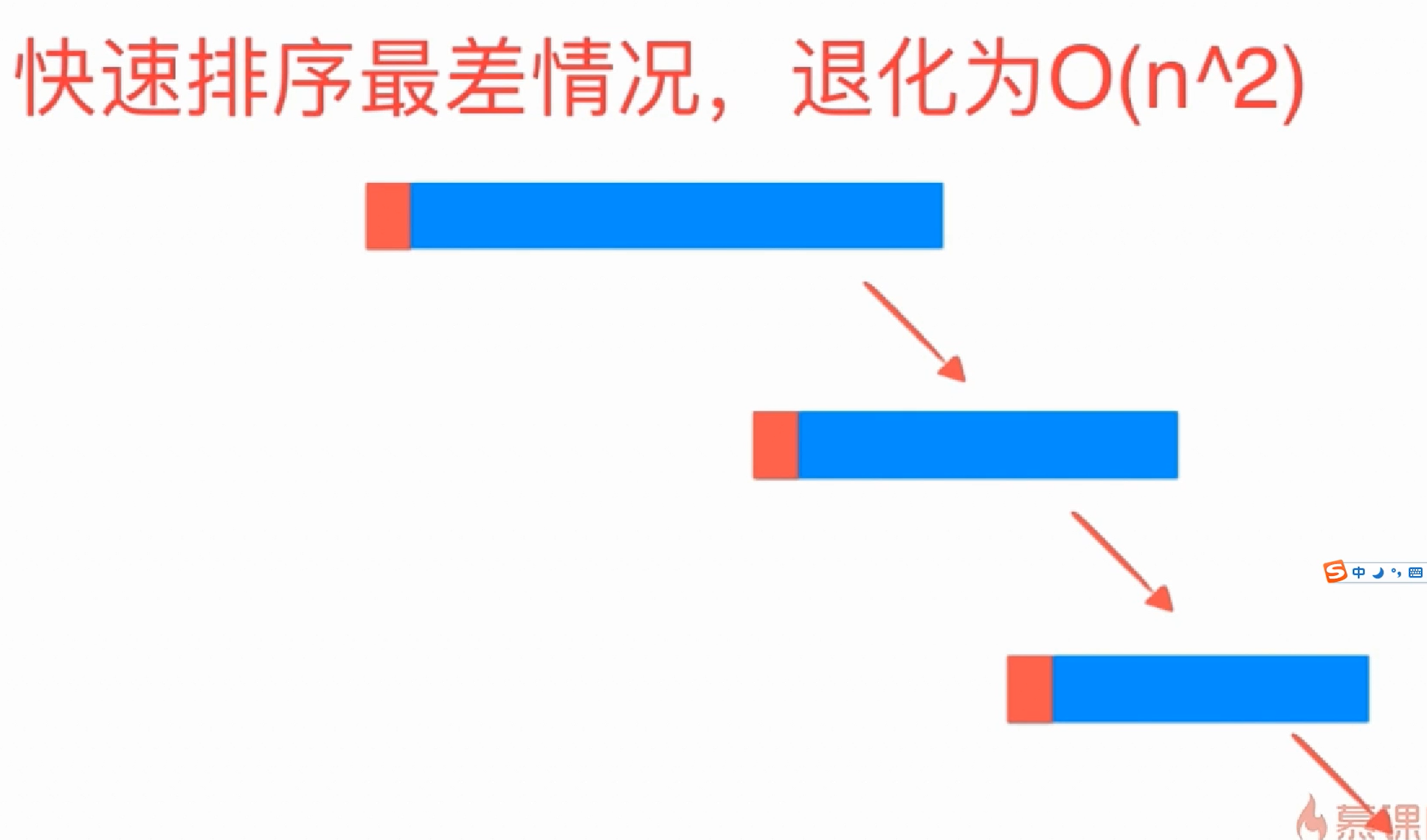
对于分治算法，当每次划分时，算法若都能分成两个等长的子序列时，那么分治算法效率会达到最大。也就是说，基准的选择是很重要的。选择基准的方式决定了两个分割后两个子序列的长度，进而对整个算法的效率产生决定性影响
所以当如果一个有序递增序列, 每次选基准都选最后一个, 那肯定效率很差了啊

普通快排

注意初始index的位置:

# partition_index 在还没开始遍历之前时应该指向待遍历元素的最左边的那个元素的前一个位置
# 在这里这种写法就是 `left_index`
# 这才符合partition_index的定义:
#       partition_index指向小于pivot的那些元素的最后一个元素,
#       即 less_than_pivots_last_elem_index
# 因为还没找到比pivot小的元素之前, 
# partition_index是不应该指向任何待遍历的元素的
partition_index = less_than_pivots_last_elem_index = left_index

i = left_index + 1  # 因为pivot_index取left_index了, 则我们从left_index+1开始遍历

下面是原代码:

python版本

def _partition(arr, left_index, right_index):
    # 选一个元素作为枢轴量,
    # 为了模拟上面这个动画演示, 这里我们选取最左边的元素
    pivot_index = left_index
    pivot = arr[pivot_index]
    # partition_index 在还没开始遍历之前时应该指向待遍历元素的最左边的那个元素的前一个位置
    # 在这里这种写法就是 `left_index`
    # 这才符合partition_index的定义:
    #       partition_index 指向小于pivot的那些元素的最后一个元素,
    #       即 less_than_pivots_last_elem_index
    # 因为还没找到比pivot小的元素之前, 
    # partition_index是不应该指向任何待遍历的元素的
    partition_index = less_than_pivots_last_elem_index = left_index

    i = left_index + 1  # 因为pivot_index取left_index了, 则我们从left_index+1开始遍历
    while i <= right_index:
        if arr[i] < pivot:
            # arr[i] 和 大于pivot的第一个元素 Q 交换(Q 亦即: 小于pivot的那些元素的最后一个元素的后面一个元素, 所以是partition + 1) 
            arr[i], arr[partition_index+1] = arr[partition_index+1], arr[i]
            partition_index += 1
        i += 1
    arr[pivot_index], arr[partition_index] = arr[partition_index], arr[pivot_index]
    return partition_index


def quick_sort(arr, left_index, right_index):
    # 如果left等于right则说明已经partition到只有一个元素了, 可以直接return了
    if not arr or left_index >= right_index:
        return
    partition_index = _partition(arr, left_index, right_index)
    # 把partition_index左边的数据再递归快排一遍
    quick_sort(arr, left_index, partition_index-1)
    quick_sort(arr, partition_index+1, right_index)

与

cpp版本

void swap_elem(int* arr, int index_a, int index_b){
  auto temp = arr[index_a];
  arr[index_a] = arr[index_b];
  arr[index_b] = temp;
}

int partition(int arr[], int left_index, int right_index){
  int p_index = left_index;
  int left_end = p_index;
  for(int i = left_index+1; i <= right_index; ++i){
    if(arr[i] < arr[p_index]){
      swap_elem(arr, i, left_end+1);
      left_end += 1;
    }
  }
  swap_elem(arr, left_end, p_index);
  return left_end;
}

void quick_sort(int* arr, int left_index, int right_index){
  if(!arr || left_index >= right_index)
    return;
  auto p_index = partition(arr, left_index, right_index);
  quick_sort(arr, left_index, p_index-1);
  quick_sort(arr, p_index+1, right_index);
}

普通快排的优化

通过快排效率很差的情况, 我们知道快排在面对已经比较有序数组的时候效率如果固定选择某个位置的pivot则性能较差, 所以我们加上两种优化方式:

• 随机选pivot
• 小数组用插排

+ import random

def _partition_optimized(arr, left_index, right_index):
    # 选一个元素作为枢轴量,
    # 为了模拟上面这个动画演示, 这里我们选取最左边的元素
    pivot_index = left_index

+   # 优化1:
+   #   随机选一个元素和最左边的交换,
+   #   配合下方的`pivot = arr[left_index]`就达到了随机选一个元素当pivot的效果
+   rand_index = random.randint(left_index, right_index)
+   arr[pivot_index], arr[rand_index] = arr[rand_index], arr[pivot_index]

    pivot = arr[pivot_index]
    # partition_index 在还没开始遍历之前时应该指向待遍历元素的最左边的那个元素的前一个位置
    # 在这里这种写法就是 `left_index`
    # 这才符合partition_index的定义:
    #       partition_indexy指向小于pivot的那些元素的最后一个元素,
    #       即 less_than_pivots_last_elem_index
    # 因为还没找到比pivot小的元素之前, 
    # partition_index是不应该指向任何待遍历的元素的
    partition_index = less_than_pivots_last_elem_index = left_index

    i = left_index + 1  # 因为pivot_index取left_index了, 则我们从left_index+1开始遍历
    while i <= right_index:
        if arr[i] < pivot:
            arr[i], arr[partition_index+1] = arr[partition_index+1], arr[i]
            partition_index += 1
        i += 1
    arr[pivot_index], arr[partition_index] = arr[partition_index], arr[pivot_index]
    return partition_index


def quick_sort_optimized(arr, left_index, right_index):
    # 如果left等于right则说明已经partition到只有一个元素了, 可以直接return了
    if not arr or left_index >= right_index:
        return
+   # 优化2:
+   #   小数组用插排
+   if (right_index - left_index) <= 15:
+       insert_sort(arr, left_index, right_index)
+       return
    partition_index = _partition(arr, left_index, right_index)
    # 把partition_index左边的数据再递归快排一遍
    quick_sort(arr, left_index, partition_index-1)
    quick_sort(arr, partition_index+1, right_index)

解决普通快排有大量相同元素时的性能问题

对于分治算法，当每次划分时，算法若都能分成两个等长的子序列时，那么分治算法效率会达到最大.
当数组中有大量相同元素的时候, 不管怎么选pivot都很容易变成下面这种情况导致分成子序列的不平衡, 这将极大的影响时间复杂度, 最差的情况会退化成O(N2)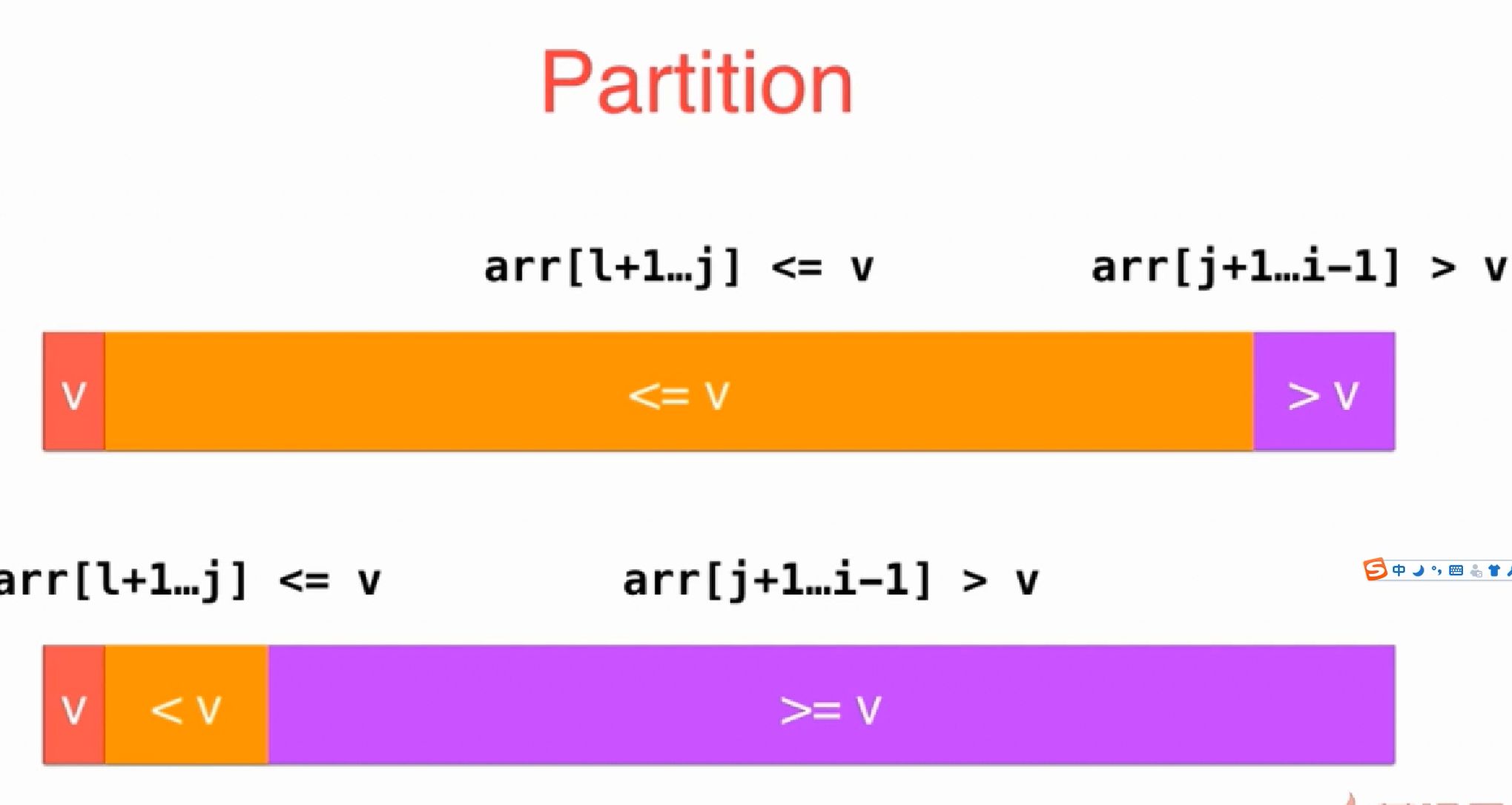

双路快排-初步解决有大量相同元素的性能问题

所以产生了双路快排的方式, 他使用两个索引值（i、j）用来遍历我们的序列，将小于等于v的元素放在索引i所指向位置的左边，而将大于等于v的元素放在索引j所指向位置的右边, 通过下图我们可以看到当等于v的情况也会发生交换, 这就基本可以保证等于v的元素也可以较为均匀的放到左右两边

待改进的地方: 还是把等于v的元素加入到了待处理的数据中, 之后又去重复计算这些等于v的元素了, 为了排除这些已经等于v的元素, 所以产生了三路快排

三路快排-完全解决有大量相同元素的性能问题

这是最经典的解决有大量重复元素的问题的快排方案, 被大多数系统所使用.

注意初始index的位置:

pivot = arr[pivot_index]
# lt_index 指向小于pivot的那些元素的最右边的一个元素,
# lt_index 即 less_than_pivots_last_elem_index
# 因为还没找到比pivot小的元素之前, 
# lt_index 是不应该指向任何待遍历的元素的, 
# gt_index 同理, gt_index指向大于pivot的那些元素的最左边的一个元素,
lt_index = less_than_pivots_last_elem_index = left_index
gt_index = right_index + 1

i = left_index + 1  # 因为pivot_index取left_index了, 则我们从left_index+1开始遍历

接下来是完整代码:

cpp版本

int* partition_3_ways(int arr[], int left_index, int right_index){
  int p_index = left_index;
  auto left_end = left_index;
  auto right_start = right_index + 1;
  for(int i=left_index + 1; i < right_start;){
    if(arr[i] < arr[p_index]){
      swap_elem(arr, i, left_end + 1);
      left_end += 1;
      ++i;
    }
    else if(arr[i] > arr[p_index]){
      swap_elem(arr, i, right_start - 1);
      right_start -= 1;
      // 注意!! 这个情况是不 `++i` 的 !
    }
    else{
      ++i;
    }
  }
  swap_elem(arr, left_end, p_index);
  int* ret_arr = new int[2];
  ret_arr[0] = left_end;
  ret_arr[1] = right_start;
  return ret_arr;
}


void quick_sort_3_ways(int* arr, int left_index, int right_index){
  if(!arr || left_index >= right_index)
    return;
  auto ret_arr = partition_3_ways(arr, left_index, right_index);
  auto left_end = ret_arr[0];
  auto right_start = ret_arr[1];
  delete[] ret_arr;
  quick_sort_3_ways(arr, left_index, left_end);
  quick_sort_3_ways(arr, right_start, right_index);
}

以及:

python版本

def quick_sort_3_ways(arr, left_index, right_index):
    # 如果left等于right则说明已经partition到只有一个元素了, 可以直接return了
    if not arr or left_index >= right_index:
        return
    if (right_index - left_index) <= 15:
        insert_sort(arr, left_index, right_index)
        return

    # 选一个元素作为枢轴量,
    # 为了模拟上面这个动画演示, 这里我们选取最左边的元素
    pivot_index = left_index
    # 随机选一个元素和最左边的交换,
    # 配合下方的`pivot = arr[left_index]`就达到了随机选一个元素当pivot的效果
    rand_index = random.randint(left_index, right_index)
    arr[pivot_index], arr[rand_index] = arr[rand_index], arr[pivot_index]
    
    pivot = arr[pivot_index]
    # lt_index 指向小于pivot的那些元素的最右边的一个元素,
    # lt_index 即 less_than_pivots_last_elem_index
    # 因为还没找到比pivot小的元素之前, 
    # lt_index 是不应该指向任何待遍历的元素的, 
    # gt_index 同理, gt_index指向大于pivot的那些元素的最左边的一个元素,
    lt_index = less_than_pivots_last_elem_index = left_index
    gt_index = right_index + 1

    i = left_index + 1  # 因为pivot_index取left_index了, 则我们从left_index+1开始遍历
    while i < gt_index:
        if arr[i] < pivot:
            arr[i], arr[lt_index+1] = arr[lt_index+1], arr[i]
            lt_index += 1
            i += 1
        elif arr[i] > pivot:  # 注意!! 这个情况是不 `i += 1` 的 !
            arr[i], arr[gt_index-1] = arr[gt_index-1], arr[i]
            gt_index -= 1
        else:
            i += 1
    arr[pivot_index], arr[lt_index] = arr[lt_index], arr[pivot_index]

    quick_sort_3_ways(arr, left_index, lt_index)
    quick_sort_3_ways(arr, gt_index, right_index)

堆排序

最大堆的堆排序之后的数组是升序, 最小堆反之.
堆排序 HeapSort 由 以下两部分组成 :

• 堆化 MaxHeapify
• 建堆 BuildMaxHeap

TopK问题

求一堆数组的最大的k个数

如果是求最大的k个数则用最小堆, 反之则用最大堆

算法的复杂度分析:
由于使用了一个大小为 k 的堆，空间复杂度为 O(k)
入堆和出堆操作的时间复杂度均为 O(logk)，每个元素都需要进行一次入堆操作，故算法的时间复杂度为 O(nlogk)

堆排序的复杂度

• 时间复杂度 :
  • MaxHeapify : O(logN).
  • BuildMaxHeap : O(N).
    看起来像是O(NlogN), 其实是O(N), 因为不同结点运行 MaxHeapify 的 时间和该结点的树高相关, 而大部分结点的高度都很小, <<算法导论>>中有相关证明
  • HeapSort : O(NlogN).
    初始化堆 BuildMaxHeap 的时间复杂度为O(N); 之后因为每次交换结点然后从堆中去掉最后一个结点后都要重建堆 BuildMaxHeap
    (上述 HeapSort 函数代码中的倒数第三行 MaxHeapify(arr, 0, --length) 其实就是个重建堆的过程) ,
    重建堆 BuildMaxHeap 的时间复杂度为O(N), 而 length - 1 次调用了 MaxHeapify, MaxHeapify 的时间复杂度为O(lgN). 所以为 O(N + NlogN), 即为O(Nlogn)
• 空间复杂度 :
  • O(1), 因为没有用辅助内存.

堆化

注意: 以下演示图中的index是从1开始的, 方便我们看动图理解堆化过程, 我们下方代码的数组的index是从0开始的

注意 :
在调用MaxHeapify的时候, 我们假定索引为index的元素的左子树和右子树都是最大堆, 不然你如果注意看的话, 你会发现上图中index为10的那个元素其实是没有计算到的, 因为我们假定以index=5为根节点的二叉树都是最大堆了, 所以无需计算他.
那为何要作如此假设呢?
因为要跟建堆 BuildMaxHeap 配合来完成堆排序, 而建堆 BuildMaxHeap是从下至上的.

动画演示如下, 比如要对17这个元素为父元素的所有子元素进行堆化:

如果是对数组的[left_index, right_index]来排序, 且数组的首index为0的话, 则:

• 最后一个非叶子节点的index为left_index + (length/2 - 1)
• left_child_index = 2 * (pending_heapify_index-left_index) + 1
• right_child_index = left_child_index + 1
  这两个index的取得方式在下方代码有体现.

堆化递归写法

递归写法更容易理解一些:

# 递归版, 对 pending_heapify_index 元素执行堆化
def _max_heapify_recursive(arr, pending_heapify_index, left_index, right_index):
    if pending_heapify_index >= right_index:  # 当满足此条件, 应该结束`_max_heapify_recursive`递归了
        return
    left_child_index = 2 * (pending_heapify_index-left_index) + 1
    right_child_index = left_child_index + 1

    # 选出 pending_heapify_index 的左右孩子中最大的元素,
    # 并与 pending_heapify_index 元素交换
    cur_max_index = pending_heapify_index
    if left_child_index <= right_index and arr[cur_max_index] < arr[left_child_index]:
        cur_max_index = left_child_index
    if right_child_index <= right_index and arr[cur_max_index] < arr[right_child_index]:
        cur_max_index = right_child_index

    # 若当前已经是最大元素了, 则停止递归, 如果不是则执行交换与继续递归
    if cur_max_index != pending_heapify_index:
        arr[pending_heapify_index], arr[cur_max_index] = arr[cur_max_index], arr[pending_heapify_index]
        _max_heapify_recursive(arr, cur_max_index, left_index, right_index)  # 继续 堆化 cur_max_index 的子元素

堆化迭代写法

# 迭代版, 对 pending_heapify_index 元素执行堆化
def _max_heapify_iterative(arr, pending_heapify_index, left_index, right_index):
    left_child_index = 2 * (pending_heapify_index-left_index) + 1
    while left_child_index <= right_index:
        right_child_index = left_child_index + 1
        # 选出 pending_heapify_index 的左右孩子中最大的元素,
        # 并与 pending_heapify_index 元素交换
        cur_max_index = pending_heapify_index
        if left_child_index <= right_index and arr[cur_max_index] < arr[left_child_index]:
            cur_max_index = left_child_index
        if right_child_index <= right_index and arr[cur_max_index] < arr[right_child_index]:
            cur_max_index = right_child_index

        # 若当前已经是最大元素了, 则直接break, 如果不是则执行交换与继续新一轮的堆化循环
        if cur_max_index != pending_heapify_index:
            arr[pending_heapify_index], arr[cur_max_index] = arr[cur_max_index], arr[pending_heapify_index]
            pending_heapify_index = cur_max_index
            left_child_index = 2 * (pending_heapify_index-left_index) + 1
        else:
            break

迭代写法的话也可以使用赋值的方式取代不断的swap,
该优化思想和我们之前对插入排序进行优化的思路是一致的, 此处这个优化代码就略了

建堆

如果是对数组的[left_index, right_index]来排序, 且数组的首index为0的话, 则最后一个非叶子节点的index为left_index + (length/2 - 1), 我们对每一个不是叶结点的元素自底向上调用一次 Max_Heapify 就可以把一个大小为 length 的数组转换为最大堆.

注意: 为了方便我们看动图理解堆化过程, 以下动画演示图中的index是从1开始的, 而我们下方代码的数组的index是从0开始的

def _build_max_heap(arr, left_index, right_index):
    # 建堆, 从最后一个非叶结点开始, 自底向上堆化就建好了一个最大堆
    root_index = left_index
    arr_len = right_index - left_index + 1
    last_none_leaf_index = root_index + (arr_len/2 - 1)

    i = last_none_leaf_index
    while i >= root_index:
        _max_heapify_recursive(arr, i, left_index, right_index)
        i -= 1

堆排序原址排序的具体实现

堆排序分两步:

1. 建堆
2. 重复以下两个操作:
   1. 把数组中的第一个元素(即根节点)也就是当前堆的最大元素逐个和数组后面的元素交换
   2. 对根节点做一次堆化操作

python版本

def heap_sort(arr, left_index , right_index):
    if not arr or left_index >= right_index or right_index <= 0:
        return
    _build_max_heap(arr, left_index, right_index)
    # 把数组中的第一个元素(即根节点)也就是当前堆的最大元素逐个和数组后面的元素交换
    # 交换后根节点已经违背最大堆性质了, 但其他的元素还是符合最大堆性质的
    # 所以然后要对根节点做一次堆化操作
    cur_right_index = right_index
    root_index = left_index
    while cur_right_index >= root_index:
        arr[root_index], arr[cur_right_index] = arr[cur_right_index], arr[root_index]
        cur_right_index -= 1
        _max_heapify_recursive(arr, root_index, left_index, cur_right_index)

与

cpp版本

void heapify(int arr[], int p_i, int left_i, int right_i){
  if(p_i > right_i)
    return;

  auto left_child_i = (p_i-left_i)*2 + 1;
  auto right_child_i = left_child_i + 1;

  auto max_child_i = p_i;
  if(left_child_i <= right_i && arr[left_child_i] > arr[max_child_i])
    max_child_i = left_child_i;
  if(right_child_i <= right_i && arr[right_child_i] > arr[max_child_i])
    max_child_i = right_child_i;

  if(max_child_i != p_i){
    swap_elem(arr, max_child_i, p_i);
    heapify(arr, max_child_i, left_i, right_i);
  }
}

void build_max_heap(int arr[], int left_i, int right_i){
  auto arr_len = right_i - left_i + 1;
  auto last_none_leaf_i = left_i + (arr_len / 2) - 1;

  while(last_none_leaf_i >= left_i){
    heapify(arr, last_none_leaf_i, left_i, right_i);
    --last_none_leaf_i;
  }
}

void heap_sort(int* arr, int left_index, int right_index){
  if(!arr)
    return;
  build_max_heap(arr, left_index, right_index);
  auto cur_right_i = right_index;
  while (cur_right_i >= left_index){
    swap_elem(arr, left_index, cur_right_i);
    --cur_right_i;
    heapify(arr, left_index, left_index, cur_right_i);
  }
}

递归解题思路

实际上，递归有两个显著的特征,终止条件和自身调用:

• 自身调用：原问题可以分解为子问题，子问题和原问题的求解方法是一致的，即都是调用自身的同一个函数。
• 终止条件：递归必须有一个终止的条件，即不能无限循环地调用本身。

递归调用可理解为入栈操作，而返回则为出栈操作。写递归算法的关键是要明确函数的「定义」是什么，然后相信这个定义，利用这个定义推导最终结果，绝不要试图跳入递归。我们千万不要跳进递归的细节里，你的脑袋才能压几个栈呀。

解决递归问题一般就三步曲，这个递归解题三板斧理解起来有点抽象，我们拿阶乘递归例子来喵喵吧~
三部曲分别是：

1. 定义函数功能
   定义函数功能，就是说，你这个函数是干嘛的，做什么事情，换句话说，你要知道递归原问题是什么呀？比如你需要解决阶乘问题，定义的函数功能就是n的阶乘，如下：

   //n的阶乘（n为大于0的自然数）
   int factorial (int n){
   
   }

2. 寻找递归终止条件
   递归的一个典型特征就是必须有一个终止的条件，即不能无限循环地调用本身。所以，用递归思路去解决问题的时候，就需要寻找递归终止条件是什么。比如阶乘问题，当n=1的时候，不用再往下递归了，可以跳出循环啦，n=1就可以作为递归的终止条件，如下：

   //n的阶乘（n为大于0的自然数）
   int factorial (int n){
       if(n==1){
       return 1;
       }
   }

3. 找出递归结构, 或者递推函数的等价关系式
   递归的「本义」，就是原问题可以拆为同类且更容易解决的子问题，即「原问题和子问题都可以用同一个函数关系表示。递推函数的等价关系式，这个步骤就等价于寻找原问题与子问题的关系，如何用一个公式把这个函数表达清楚」。阶乘的公式就可以表示为 f(n) = n * f(n-1), 因此，阶乘的递归程序代码就可以写成这样，如下：

   int factorial (int n){
       if(n==1){
       return 1;
       }
       return n * factorial(n-1);
   }

「注意啦」，不是所有递推函数的等价关系都像阶乘这么简单，一下子就能推导出来。需要我们多接触，多积累，多思考，多练习递归题目滴~

递归与二叉树

递归，是使用计算机解决问题的一种重要的思考方式。而二叉树由于其天然的递归结构，使得基于二叉树的算法，均拥有着递归性质。使用二叉树，是研究学习递归算法的最佳入门方式。在这一章里，我们就来看一看二叉树中的递归算法。

二叉树递归技巧

• 如果采用前序遍历的递归形式解题, 则其实是从二叉树的顶部到底部来操作的, 脑海中得有这么一个想象, 从上到下访问每个结点之前做事
• 如果采用后序遍历的递归形式解题, 则其实是从二叉树的底部到顶部来操作的, 从下到上访问每个结点之后做事
• 一般很少用中序形式解题

lc236-LCA最近公共祖先问题

lc236, 给出一棵二叉树的根节点，现在有这个二叉树的部分节点，要求这些节点最近的公共祖先

• 参考此处
• 参考

这道题目刷过的同学未必真正了解这里面回溯的过程，以及结果是如何一层一层传上去的。那么我给大家归纳如下三点：

• 求最小公共祖先，需要从底向上遍历，那么二叉树，只能通过后序遍历（即：回溯）实现从低向上的遍历方式。
• 在回溯的过程中，必然要遍历整颗二叉树，即使已经找到结果了，依然要把其他节点遍历完，因为要使用递归函数的返回值（也就是代码中的left和right）做逻辑判断。
• 要理解如果返回值left为空，right不为空为什么要返回right，为什么可以用返回right传给上一层结果。

可以说这里每一步，都是有难度的，都需要对二叉树，递归和回溯有一定的理解。

若 root 是 p,q 的 最近公共祖先 ，则只可能为以下情况之一：

• p 和 q 在 root 的子树中，且分列 root 的 异侧（即分别在左、右子树中）；
• p=root ，且 q 在 root 的左或右子树中；
• q=root ，且 p 在 root 的左或右子树中；

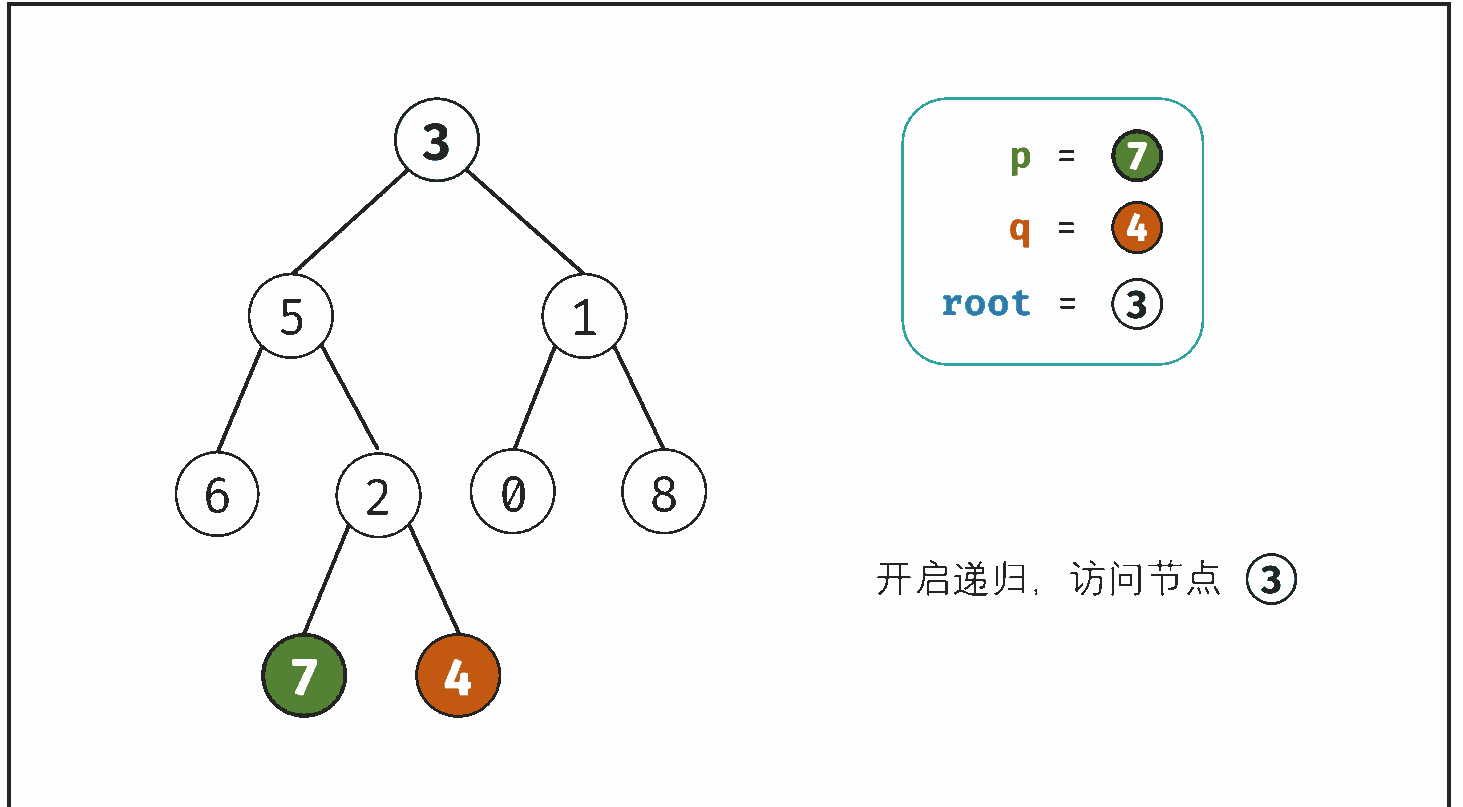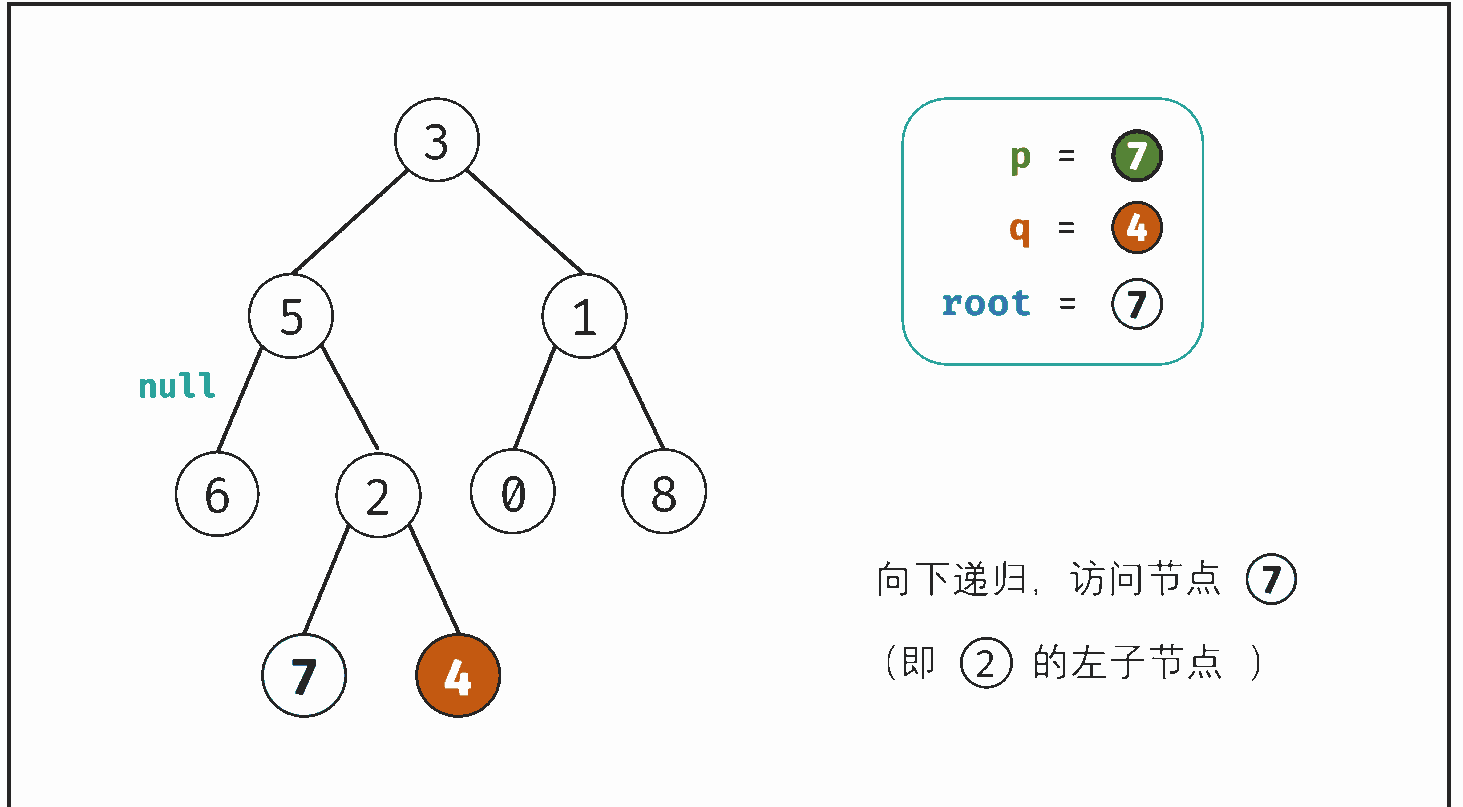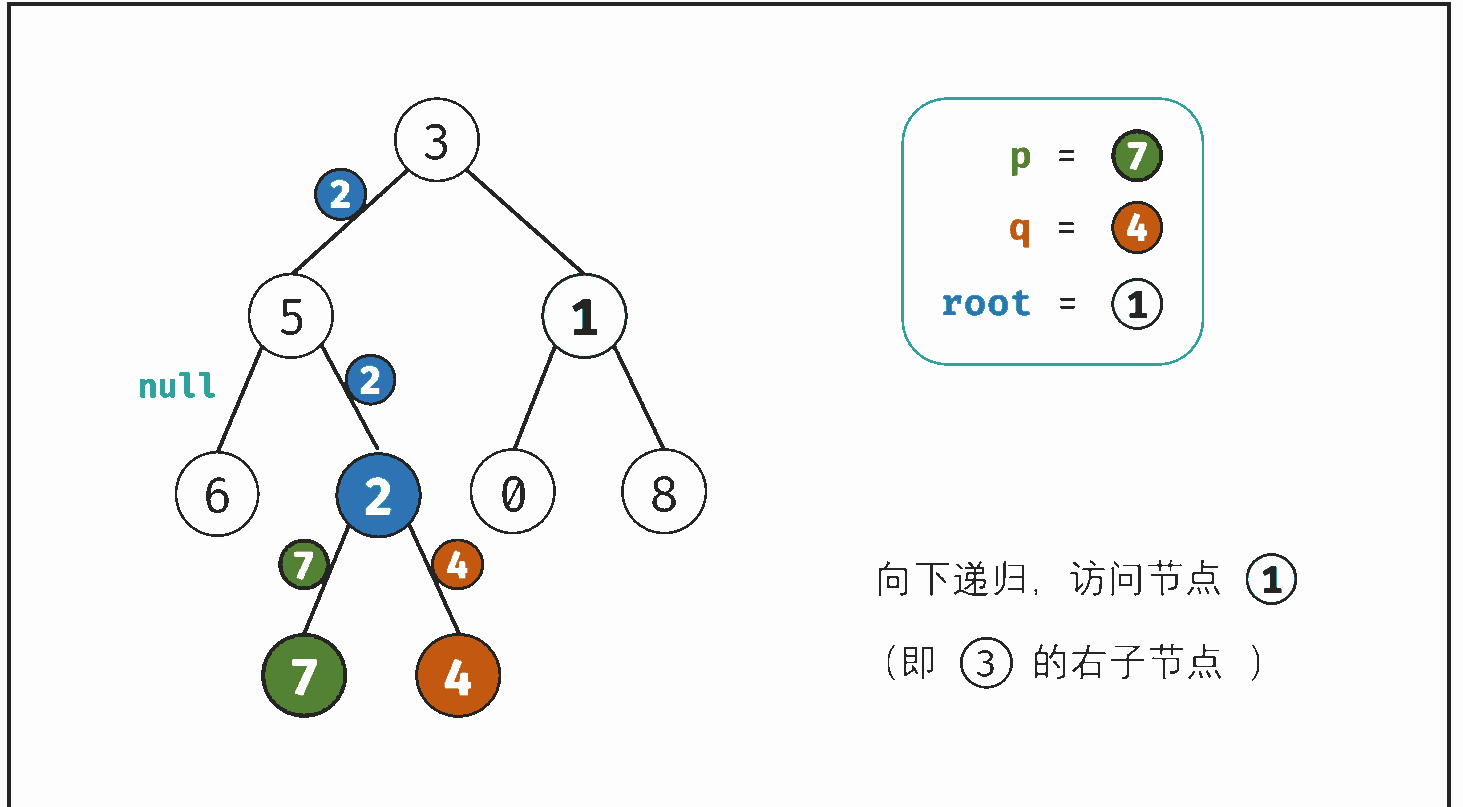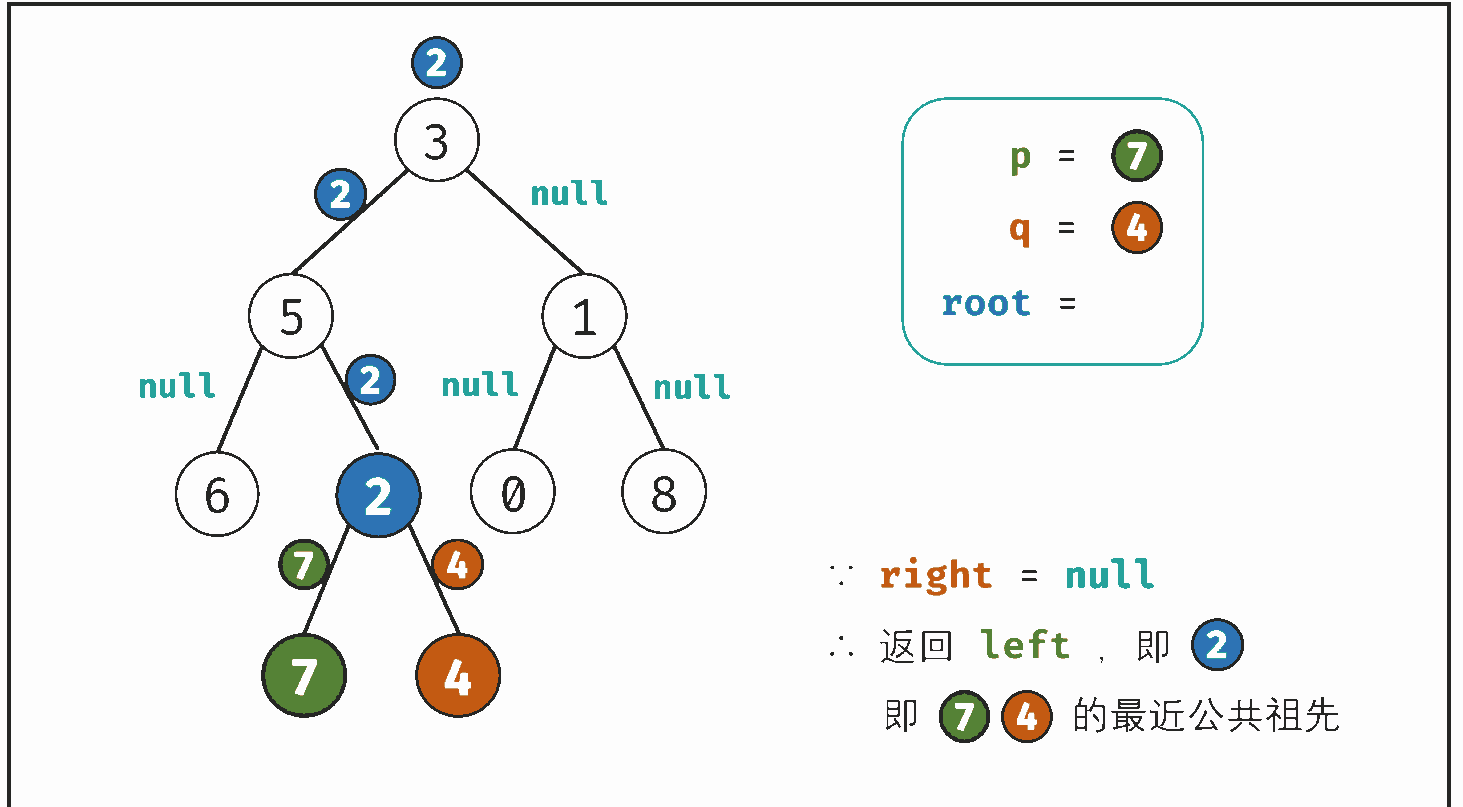
考虑通过递归对二叉树进行后序遍历，当遇到节点 p 或 q 时返回。从底至顶回溯，当节点 p,q 在节点 root 的异侧时，节点 root 即为最近公共祖先，则向上返回 root 。

递归解析：

• 终止条件：
  • 当越过叶节点，则直接返回 null ；
  • 当 root 等于 p,q ，则直接返回 root ；
• 递推工作：
  • 开启递归左子节点，返回值记为 left ；
  • 开启递归右子节点，返回值记为 right ；
• 返回值： 根据 left 和 right ，可展开为四种情况；
  • 1. 当 left 和 right 同时为空 ：说明 root 的左 / 右子树中都不包含 p,q ，返回 null ；
  • 2. 当 left 和 right 同时不为空 ：说明 p,q 分列在 当前 root 的 异侧 （分别在 左 / 右子树），因此 当前的root 为p/g最近公共祖先，返回 root ；
  • 3. 当 left 为空 ，right 不为空 ：p,q 都不在 root 的左子树中，直接返回 right ,具体可分为两种情况：
    • p,q 其中一个在 root 的 右子树 中，此时 right 指向 p（假设为 p ）
    • p,q 两节点都在 root 的 右子树 中，此时的 right 指向 最近公共祖先节点
  • 4. 当 left 不为空 ， right 为空 ：与情况 3. 同理；

代码如下:

class Solution_LCA(object):
    def lowestCommonAncestor(self, root, p, q):
        """
        :type root: TreeNode
        :type p: TreeNode
        :type q: TreeNode
        :rtype: TreeNode
        """
        if root == p or root == q:  # 找到p或q了, 则返回p或q
            return root
        # 没找到p或q, 而且已经找到底, 越过叶子节点了, 则返回None
        if root is None:
            return None
        # 到 左子树 去找
        left_child_find_res = self.lowestCommonAncestor(root.left, p, q)
        # 到 右子树 去找
        right_child_find_res = self.lowestCommonAncestor(root.right, p, q)
        if not left_child_find_res:
            # 当 left 为空 ，right 不为空 ：p,q 都不在 root 的左子树中，直接返回 right
            return right_child_find_res
        if not right_child_find_res:
            return left_child_find_res
        # 当 left 和 right 同时不为空 ：
        # 说明 p,q 分列在 当前 root 的 异侧 （分别在 左 / 右子树），
        # 因此 当前的root 为p/g最近公共祖先，返回 root ；
        return root

lc106-后序中序求原二叉树

• leetcode106题后序中序求原二叉树
• 参考: https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solution/

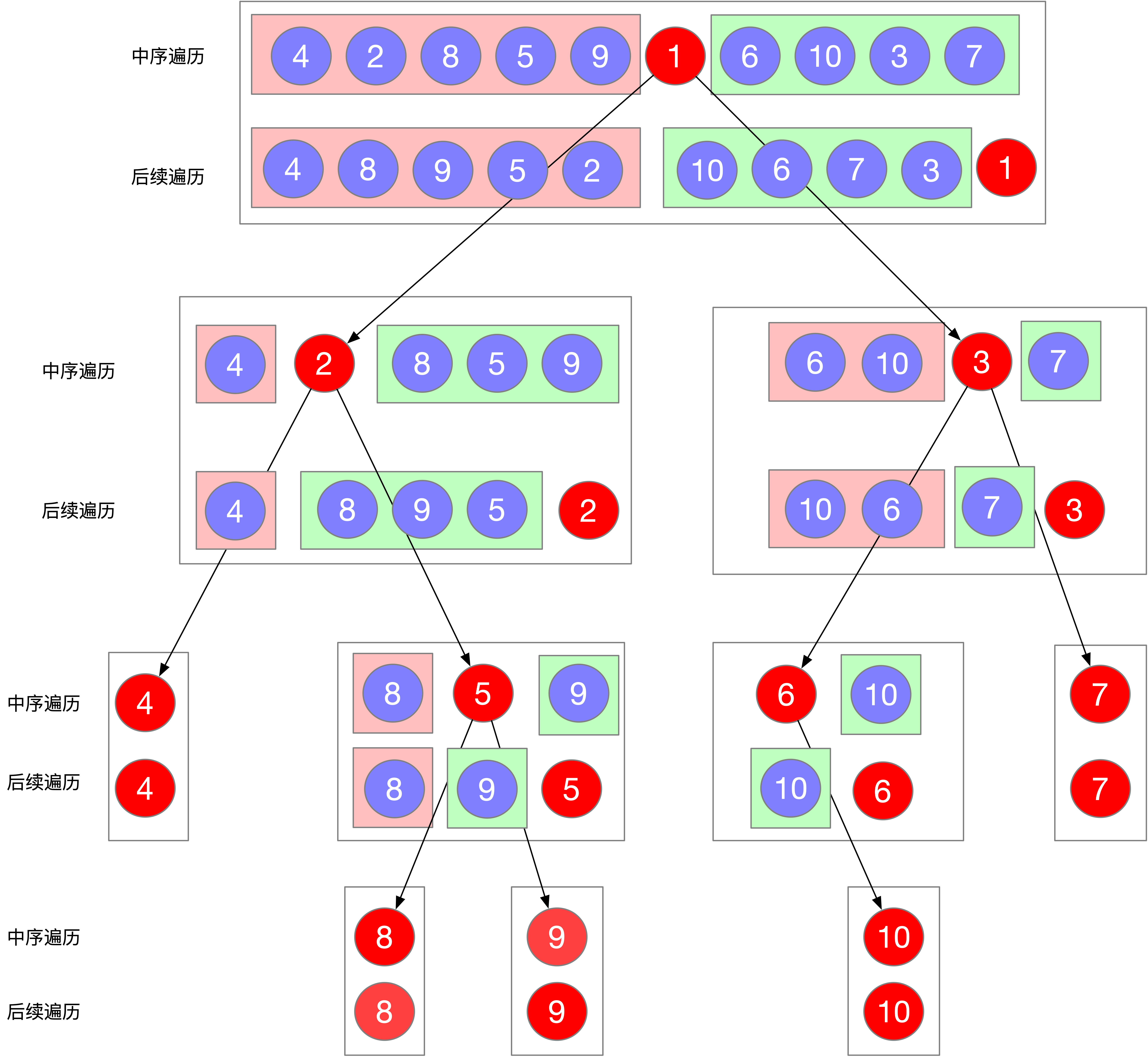
首先来看题目给出的两个已知条件 中序遍历序列 和 后序遍历序列 根据这两种遍历的特性我们可以得出三个结论

• 在后序遍历序列中,最后一个元素为树的根节点
• 在中序遍历序列中,根节点的左边为左子树(设其长度为len_left), 根节点的右边为右子树
• 当前后序遍历序列中[postorder_left_index...len_left-1]为左子树的结点, 其他的除最后一个结点外都是右子树的结点

则代码如下:

class Solution_build_bt(object):
    def buildTree(self, inorder, postorder):
        """
        :type inorder: List[int]
        :type postorder: List[int]
        :rtype: TreeNode
        """
        if not inorder or not postorder:
            return None

        def _proc_order_arr(
                inorder_left_index, inorder_right_index, 
                postorder_left_index, postorder_right_index):       
            if inorder_left_index > inorder_right_index or \
                    postorder_left_index > postorder_right_index:
                return None
            # 在后序遍历序列中,最后一个元素为树的根节点
            root_val = postorder[postorder_right_index] 
            root_inorder_index = inorder.index(root_val)
            _len_left_child = root_inorder_index-inorder_left_index
            root_node = TreeNode(root_val)
            
            # 在中序遍历序列中,根节点的左边为左子树(设其长度为len_left), 根节点的右边为右子树
            # 当前后序遍历序列中`[postorder_left_index...len_left-1]`为左子树的结点, 
            # 其他的除最后一个结点外都是右子树的结点
            root_node.left = _proc_order_arr(
                inorder_left_index,
                root_inorder_index-1,
                postorder_left_index,
                postorder_left_index + (_len_left_child-1)
            )
            root_node.right = _proc_order_arr(
                root_inorder_index+1,
                inorder_right_index,
                postorder_left_index+(_len_left_child),
                postorder_right_index-1
            )
            return root_node
            
        return _proc_order_arr(0, len(inorder)-1, 0, len(postorder)-1)

lc112-path-sum

leetcode112题

技巧: 首先要明确此递归函数的定义: 查看root是否为叶子结点并且root的val是否等于sum_num, 然后才开始写代码

# 首先要明确此递归函数的定义: 查看root是否为叶子结点并且root的val是否等于sum_num,
# 然后才开始写代码
def has_path_sum(root, sum_num):
    if not root:
        return False
    # 判断是否为叶子
    if not root.left and not root.left and root.val == sum_num:
        return True
    # 通过递归, 继续查看左右孩子节点是否有 sum_num-root.val
    if has_path_sum(root.left, sum_num-root.val):
        return True
    return has_path_sum(root.right, sum_num-root.val)

lc257-binary-tree-paths

lc257

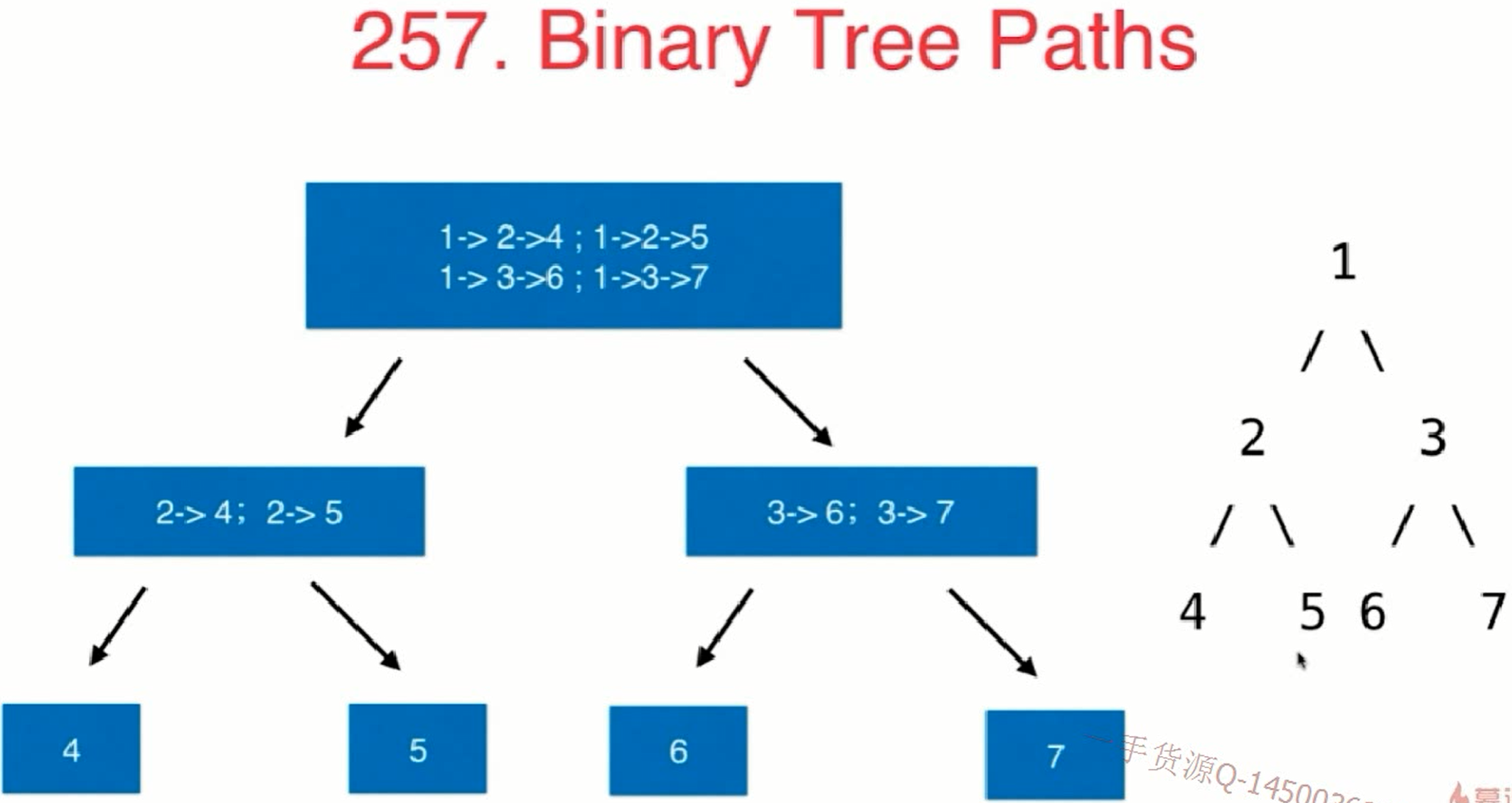
def binary_tree_paths(root):
    result_arr = []
    if not root:
        return result_arr
    if not root.left and not root.right:
        result_arr.append(str(root.val))
        return result_arr
    # 获取左孩子的路径
    left_bt_path_arr = binary_tree_paths(root.left)
    for _path in left_bt_path_arr:
        result_arr.append(str(root.val) + "->" + _path)
    # 获取右孩子的路径
    right_bt_path_arr = binary_tree_paths(root.right)
    for _path in right_bt_path_arr:
        result_arr.append(str(root.val) + "->" + _path)
    return result_arr

lc437-path-sum-3

leetcode437题
给出一颗二叉树以及一个数字sum, 判断在这棵二叉树上存在多少条路径, 其路径上的所有节点和为sum.

• 其中路径不一定要起始于根节点, 终止于叶子节点
• 路径可以从任意节点开始, 但是只能是向下走的

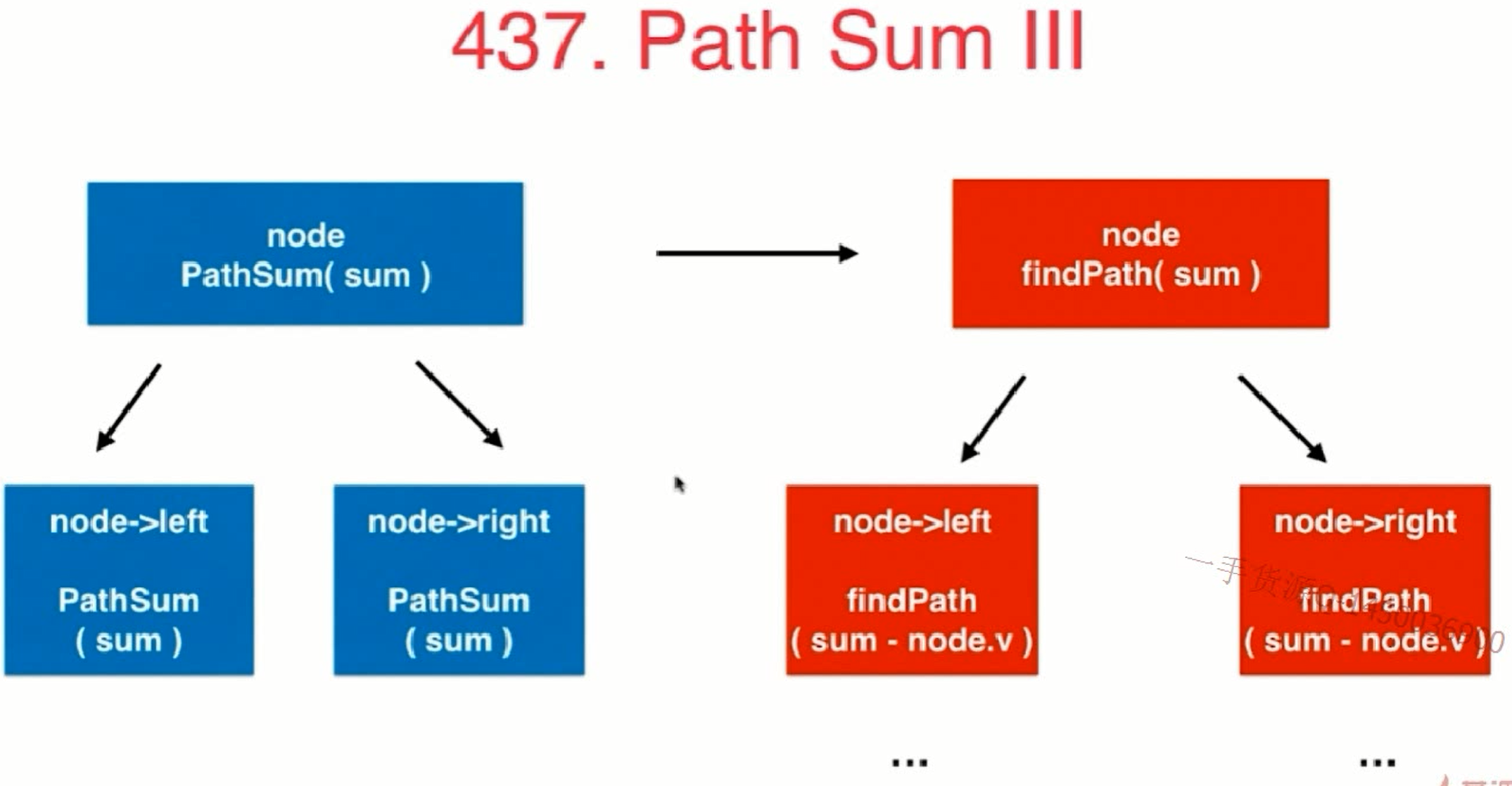
def path_sum_3(root, sum_num):
    if not root:
        return 0
    path_cnt = 0
    # 先求包括node本身的情况, 此时这轮递归所说的node是代码中的root
    # 这种情况可以用类似于 path_sum问题 的 `has_path_sum`来实现
    path_cnt += _get_path_sum_include_node(root, sum_num)
    # 再求不包括node本身的情况, 
    # 直接计算左右孩子往下的路径中和为sum_num(注意不是sum_num-root.val)的路径数量
    path_cnt += path_sum_3(root.left, sum_num)
    path_cnt += path_sum_3(root.right, sum_num)
    return path_cnt


def _get_path_sum_include_node(node, sum_num):
    if not node:
        return 0
    _path_cnt = 0
    if node.val == sum_num:  # node本身值等于sum_num也算一条路径
        _path_cnt += 1
    _path_cnt += _get_path_sum_include_node(node.left, sum_num-node.val)
    _path_cnt += _get_path_sum_include_node(node.right, sum_num-node.val)
    return _path_cnt

进阶-求path-sum-3的所有路径

leetcode437题改一下, 改成:
给出一颗二叉树以及一个数字sum, 请给出在这棵二叉树上的所有路径, 其路径上的所有节点和为sum.

• 其中路径不一定要起始于根节点, 终止于叶子节点
• 路径可以从任意节点开始, 但是只能是向下走的

根据本文lc437-path-sum-3的思路我们可以得到代码, 注意查看下方代码中的注释.

class Solution_sum_paths(object):
    def sum_paths(self, root, sum):
        if not root:
            return []
        path_arr = []
        # 先求包括node本身的情况, 此时这轮递归所说的node是代码中的root
        # 再求不包括node本身的情况, 左右孩子的情况, 
        # 这样也就达到了把每个结点都当做是root然后向下寻找路径的目的
        path_arr.extend(self._get_sum_paths(root, sum))
        path_arr.extend(self.sum_paths(root.left, sum))
        path_arr.extend(self.sum_paths(root.right, sum))
        return path_arr

    def _get_sum_paths(self, cur_root, sum_num):
        if not cur_root:
            return []
        path_str_arr = []
        # if sum_num == 0: 
        #     pass  # 不能这么写, 这么写的话, 拿不到之前的那个 cur_root 了
        if sum_num - cur_root.val == 0:  # 此时就已经找到了一个解
            path_str_arr.append(str(cur_root.val))
            return path_str_arr

        left_path_str_arr = self._get_sum_paths(cur_root.left, sum_num-cur_root.val)
        for _cur_path_str in left_path_str_arr:
            path_str_arr.append(str(cur_root.val) + "->" + _cur_path_str)

        right_path_str_arr = self._get_sum_paths(cur_root.right, sum_num-cur_root.val)
        for _cur_path_str in right_path_str_arr:
            path_str_arr.append(str(cur_root.val) + "->" + _cur_path_str)

        return path_str_arr

lc114-二叉树展开为链表

lc114
给定一个二叉树，原地将它展开为一个单链表。
例如，给定二叉树

    1
   / \
  2   5
 / \   \
3   4   6

将其展开为：

1
 \
  2
   \
    3
     \
      4
       \
        5
         \
          6

我们尝试给出这个函数的定义：
给flatten函数输入一个节点root，那么以root为根的二叉树就会被拉平为一条链表。
我们再梳理一下，如何按题目要求把一棵树拉平成一条链表？很简单，以下流程：

1. 将root的左子树和右子树拉平。
2. 将root的右子树连接到左子树下方，然后将整个左子树作为右子树。

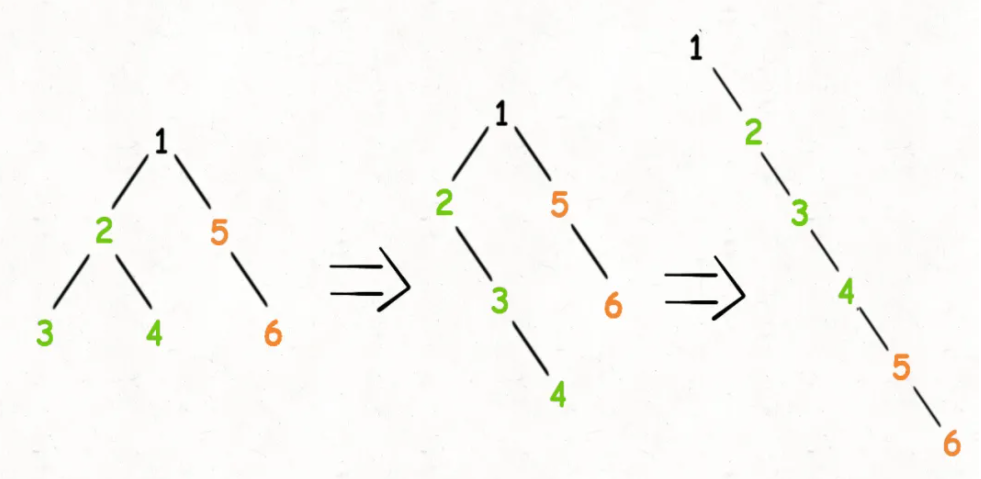
你看，这就是递归的魅力，你说flatten函数是怎么把左右子树拉平的？不容易说清楚，但是只要知道flatten的定义如此，相信这个定义，让root做它该做的事情，然后flatten函数就会按照定义工作。
另外注意递归框架是后序遍历，因为我们要从底到顶的来做拉平/连接操作。

class Solution_lc114(object):
    # [lc114](https://leetcode-cn.com/problems/flatten-binary-tree-to-linked-list/)
    def flatten(self, root):
        """
        :type root: TreeNode
        :rtype: None Do not return anything, modify root in-place instead.
        """ 
        if not root:
            return
        self.flatten(root.left)
        self.flatten(root.right)
        temp_left = root.left
        temp_right = root.right

        # 将左子树作为右子树
        root.left = None
        root.right = temp_left

        root_r = root
        # 将左子树作为右子树
        while (root_r.right):
            root_r = root_r.right
        root_r.right = temp_right

递归与回溯

参考: https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/

回溯法 采用试错的思想，它尝试分步的去解决一个问题。在分步解决问题的过程中，当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候，它将取消上一步甚至是上几步的计算，再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现，在反复重复上述的步骤后可能出现两种情况：

• 找到一个可能存在的正确的答案；
• 在尝试了所有可能的分步方法后宣告该问题没有答案。

回溯法是解决很多算法问题的常见思想，甚至可以说是传统人工智能的基础方法。其本质依然是使用递归的方法在树形空间中寻找解。在这一章，我们来具体看一下将递归这种技术使用在非二叉树的结构中，从而认识回溯这一基础算法思想,

其实上一节的二叉树与递归也是回溯的思想, 不过我们通常把回溯这个名词用在表示递归查找解的问题上

比如下面这个树形问题电话号码字母组合, 如果n是一个固定的数比如为8, 其实我们可以使用8重循环来解决, 但是n是不固定了, 所以我们只能使用回溯法来解决, 回溯法是暴力解法的一个主要手段.

动态规划其实可以算是回溯法的基础上一种改进, 同时要发现一个递归结构, 以及其他的特点就可以用回溯法, 其实回溯法也可以剪枝来优化, 不用到达所有的叶子结点从而提升我们回溯法的运行效率.

回溯算法框架

参考

废话不多说，直接上回溯算法框架。解决一个回溯问题，实际上就是一个决策树的遍历过程。你只需要思考 3 个问题：

1. 路径: 也就是已经做出的选择。
2. 选择列表: 供选择的列表
3. 结束条件: 也就是到达决策树底层，无法再做选择的条件。

如果你不理解这三个词语的解释，没关系，我们后面会用「全排列」和「N 皇后问题」这两个经典的回溯算法问题来帮你理解这些词语是什么意思，现在你先留着印象。

代码方面，回溯算法的框架：

result = []
def backtrack(供选择的列表, 选择的路径中间状态):
    if 满足结束条件:
        result.add(选择的路径中间状态)
        return
    
    for 选择 in 供选择的列表:
        做选择
        backtrack(选择的路径中间状态, 供选择的列表)
        撤销选择

其核心就是 for 循环里面的递归，在递归调用之前「做选择」，在递归调用之后「撤销选择」，特别简单。
写 backtrack 函数时，需要维护走过的「路径」和当前可以做的「选择列表」，当触发「结束条件」时，将「路径」记入结果集。

排列问题合集

排列问题代码模板

和本文的lc46-经典全排列基本一致.

lc46-经典全排列

leetcode46题:
给定一个整型数组, 其中的元素各不相同, 求返回这些元素的所有排列.
如对于 [1, 2, 3], 则返回 [ [1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1] ]

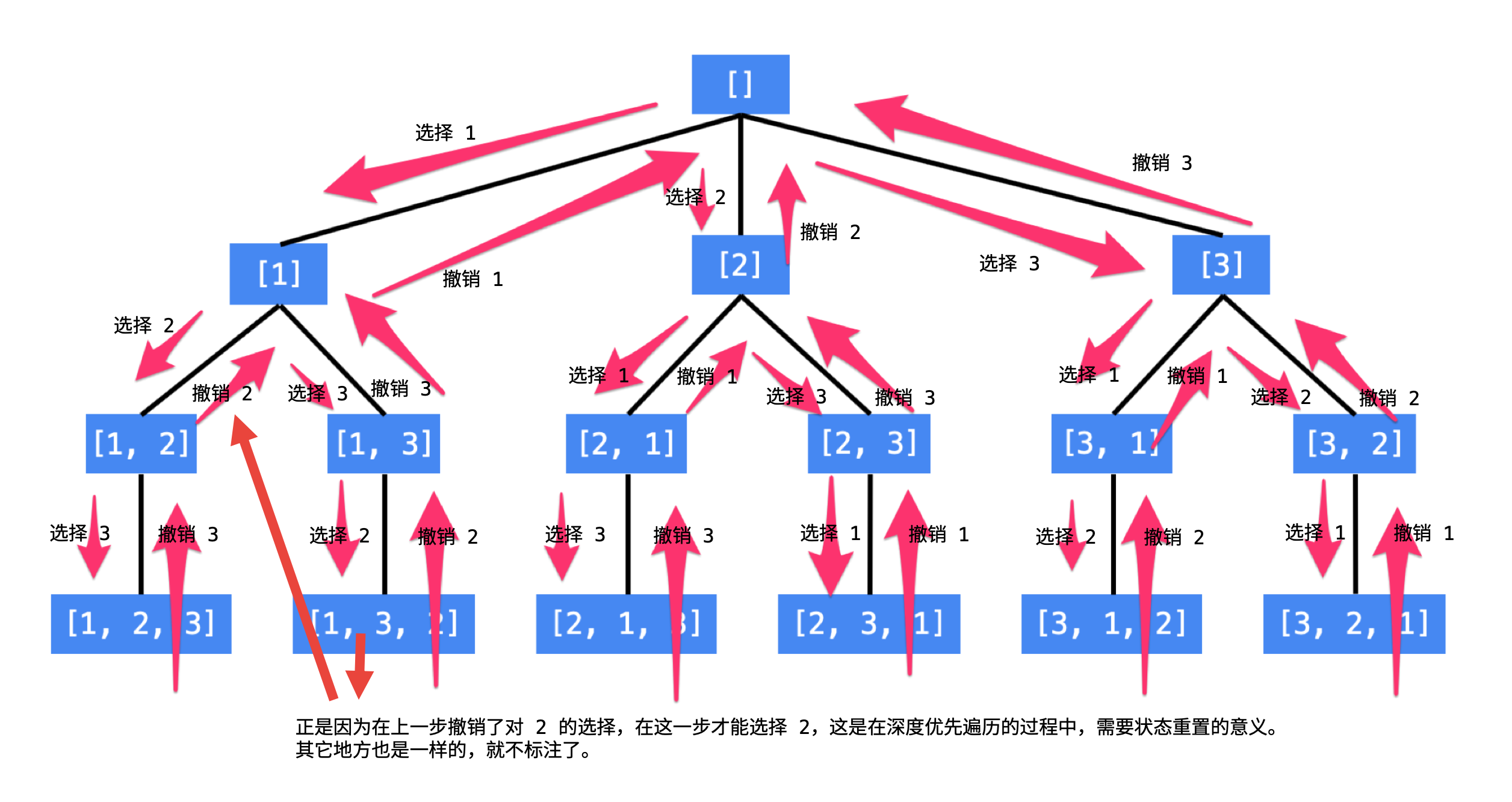
设计状态变量:

• 参考
• 首先这棵树除了根结点和叶子结点以外，每一个结点做的事情其实是一样的，即：在已经选择了一些数的前提下，在剩下的还没有选择的数中，依次选择一个数，这显然是一个 递归 结构；
• 递归的终止条件是： 一个排列中的数字已经选够了 ，因此我们需要一个变量来表示当前程序递归到第几层，我们把这个变量叫做 cnt ，每次往middle_state_container里添加元素cnt就加1, 当cnt等于全排列长度则递归终止. 当然也可以不用cnt, 每次直接if len(middle_state_container) == len(pending_proc_num_arr)也是可以的, 只是这样性能不高
• 布尔数组 used，初始化的时候都为 false 表示这些数还没有被选择，当我们选定一个数的时候，就将这个数组的相应位置设置为 true ，这样在考虑下一个位置的时候，就能够以 O(1)O(1) 的时间复杂度判断这个数是否被选择过，这是一种「以空间换时间」的思想。
  这些变量称为「状态变量」，它们表示了在求解一个问题的时候所处的阶段。需要根据问题的场景设计合适的状态变量。

注意查看下方代码中的 _generate_permutation, 排列问题基本都是这种代码写法模板.

class Solution_lc46(object):
    # [lc46](https://leetcode-cn.com/problems/permutations/)
    def __init__(self):
        self._used = []

    def permute(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        middle_arr = []
        res_arr = []
        self._used = [ False for _ in range(len(nums)) ]
        self._generate_permutation(nums, 0, res_arr, middle_arr)
        return res_arr

    def _generate_permutation(
            self, nums, cnt, res_arr, middle_arr):
        if cnt == len(nums):
            # 当cnt等于数字字符串长度的时候说明一轮已经递归到底了,
            # 则当前的 中间状态保存器 middle_state_container 则为一个解
            # 此处需要深拷贝一下, 因为下方代码有个 `middle_state_container.pop(-1)`
            res_arr.append(copy.deepcopy(middle_arr))
            return
        for i in range(len(nums)):
            if self._used[i]:
                # 如果本轮递归 used_num_set 已经有_single_num 了, 
                # 说明当前排列 middle_state_container 中已经有 _single_num 了
                # 那不应该再加入到这个排列中了
                continue
            self._used[i] = True
            middle_arr.append(nums[i])
            self._generate_permutation(
                nums,
                cnt+1,
                res_arr, middle_arr)
            # 本轮递归完毕后要清空相应记录的状态, 这就是回溯, 
            # 递归本身会记录一些状态当退出的时候他会自动清除状态, 
            # 那我们自己额外记录的状态, 比如 self._used_num_set 和
            # middle_state_container 的状态应该自己手动清除
            middle_arr.pop(-1)
            self._used[i] = False

进阶-lc47-全排列2

lc47
给定一个可包含重复数字的序列，返回所有不重复的全排列。
示例:
输入: [1,1,2]
输出:

[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

参考链接
我们先对数组排序, 然后就方便做剪枝了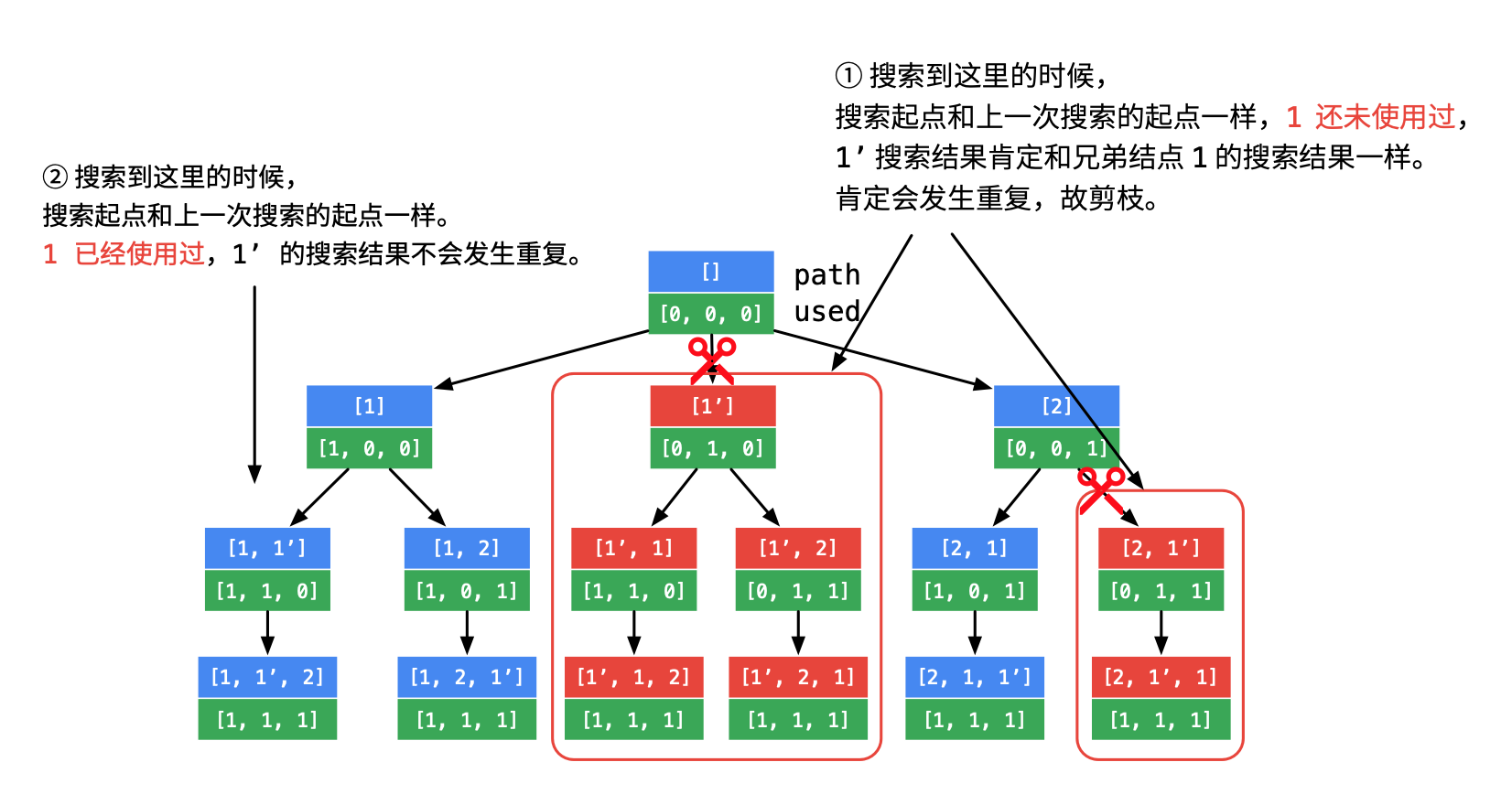

相较lc46, 代码diff如下:

class Solution_lc47(object):
    # [lc47](https://leetcode-cn.com/problems/permutations-ii)
    def __init__(self):
        self._used = []

    def permuteUnique(self, nums):
        """
        :type nums: List[int]
        :rtype: List[List[int]]
        """
        middle_arr = []
        res_arr = []
+       nums.sort()
        self._used = [ False for _ in range(len(nums)) ]
        self._generate_permutation(nums, 0, res_arr, middle_arr)
        return res_arr

    def _generate_permutation(
            self, nums, cnt, res_arr, middle_arr):
        if cnt == len(nums):
            # 当cnt等于数字字符串长度的时候说明一轮已经递归到底了,
            # 则当前的 中间状态保存器 middle_state_container 则为一个解
            # 此处需要深拷贝一下, 因为下方代码有个 `middle_state_container.pop(-1)`
            res_arr.append(copy.deepcopy(middle_arr))
            return
        for i in range(len(nums)):
            if self._used[i]:
                # 如果本轮递归 used_num_set 已经有_single_num 了, 
                # 说明当前排列 middle_state_container 中已经有 _single_num 了
                # 那不应该再加入到这个排列中了
                continue
+           # 剪枝条件：i > 0 是为了保证 nums[i - 1] 有意义
+           # 因为我们上对nums数组排序了, 
+           # 所以可以写 `self._used[i-1] == False` 是因为
+           # nums[i - 1] 在深度优先遍历的过程中刚刚被撤销选择
+           if self._used[i-1] == False and (i > 0 and nums[i] == nums[i-1]):
+              continue
            self._used[i] = True
            middle_arr.append(nums[i])
            self._generate_permutation(
                nums,
                cnt+1,
                res_arr, middle_arr)
            # 本轮递归完毕后要清空相应记录的状态, 这就是回溯, 
            # 递归本身会记录一些状态当退出的时候他会自动清除状态, 
            # 那我们自己额外记录的状态, 比如 self._used_num_set 和
            # middle_state_container 的状态应该自己手动清除
            middle_arr.pop(-1)
            self._used[i] = False

比狗-多数组且元素间有顺序要求的全排列

不用管第一题, 我们做第二题,
思路: 这类问题我们先把多个数组合并且保留各个元素对应原数组的index信息, 然后用合并后的数组做全排列并剪枝剪掉那些不符合顺序性要求的枝即可.
代码如下:

class Solution_bigo_thread_permute(object):
    def __init__(self):
        self._used = None
        self._thread_str_arr = [["A", "B", "C", "D"], ["E", "F", "G", "H"]]
        # self._thread_str_arr = [["A", "B"], ["E"]]

    def bigo_thread_permute(self):
        middle_arr = []
        res_arr = []
        # 方便精准的查询每个字母是否被使用以及
        # 方便保证abcd和efgh各自的顺序性时剪枝
        self._used = [
            [False for _ in range(len(self._thread_str_arr[i])) ]
            for i in range(len(self._thread_str_arr))
        ]
        _str_2_index_map = {}
        for i, _sub_arr in enumerate(self._thread_str_arr):
            for j, _str in enumerate(_sub_arr):
                # 存好str和他们的数组的index的对应关系
                _str_2_index_map[_str] = [i, j]
        self._generate_permute(_str_2_index_map, 0, res_arr, middle_arr)
        return res_arr

    def _generate_permute(self, str_2_index_map, cnt, res_arr, middle_arr):
        if cnt == len(str_2_index_map):
            res_arr.append(copy.deepcopy(middle_arr))
            return
        for _str, _index_list in str_2_index_map.iteritems():
            i = _index_list[0]
            j = _index_list[1]
            # 剪枝: 为了保证abcd和efgh各自的顺序性, 
            # 拿当前的j和used多维数组里i数组里的已经use的最大的max_j来作比较
            # 如果小于等于则剪枝, 
            # j大于max_j才能保证添加到middle_arr里的abcd和efgh各自的顺序性
            if j <= self._get_used_max_index_j(i):
                continue
            if self._used[i][j]:
                continue
            self._used[i][j] = True
            middle_arr.append(_str)
            self._generate_permute(str_2_index_map, cnt+1, res_arr, middle_arr)
            middle_arr.pop(-1)
            self._used[i][j] = False

    def _get_used_max_index_j(self, i):
        _max_index_j = -1
        for _cur_index_j, _is_used in enumerate(self._used[i]):
            if _is_used:
                _max_index_j = _cur_index_j
        return _max_index_j

树形问题电话号码字母组合

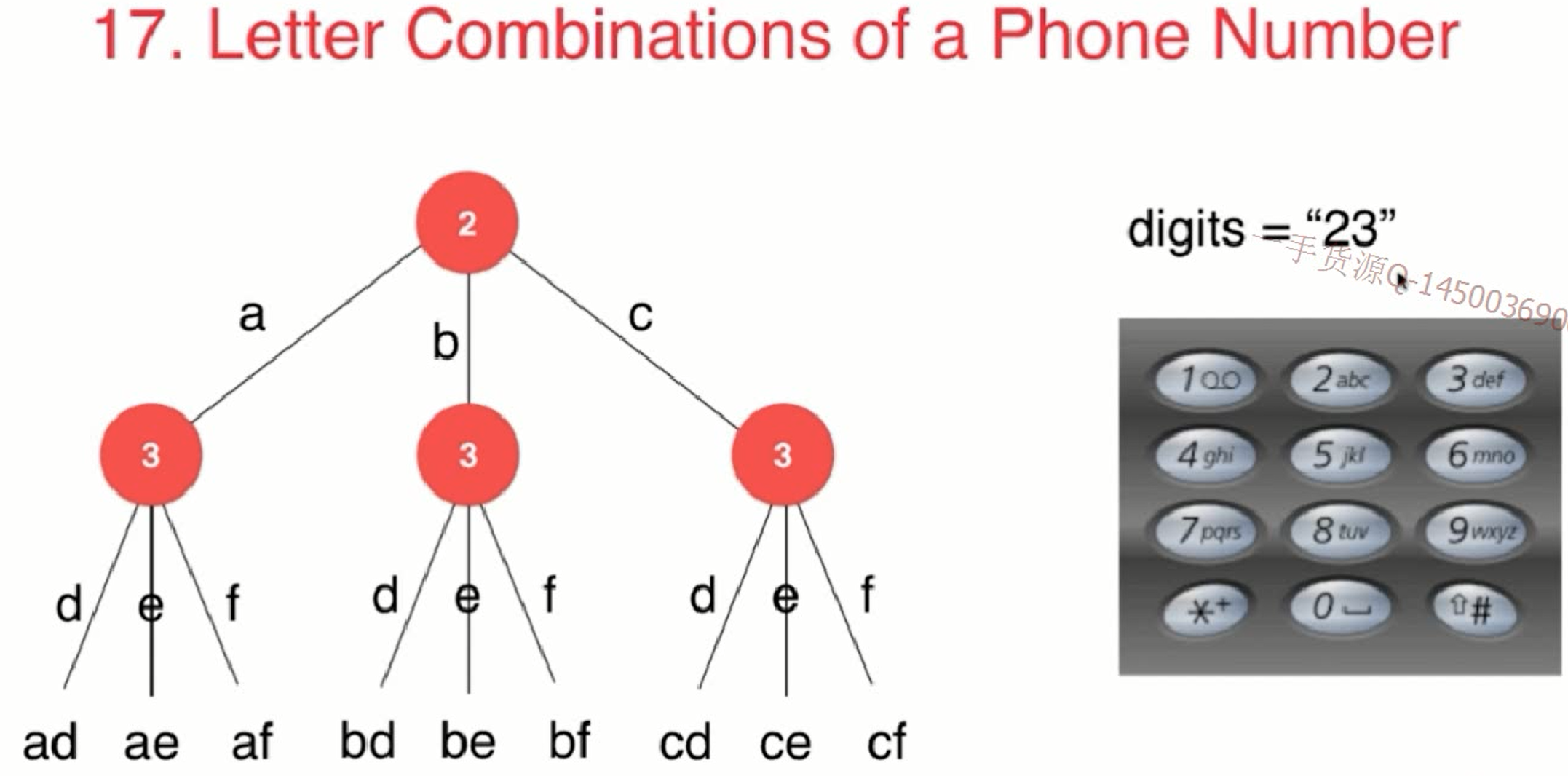
递归关系式:

• digits 是数字字符串
• s(digits) 是 digits 所能代表的字母字符串
• 则关系式如下:

  s(digits[0...n-1])
      = letter(digits[0]) + s(digits[1...n-1])
      = letter(digits[0]) + letter(digits[1]) + s(digits[2...n-1])
      = ...

这道题虽然叫字母组合问题, 但实际上是个排列问题.
注意查看下方代码中的 _get_letter_combination, 排列问题基本都是这种代码写法模板.

实现代码如下:

digits_map = {
    "0": " ",
    "1": "",
    "2": "abc",
    "3": "def",
    "4": "ghi",
    "5": "jkl",
    "6": "mno",
    "7": "pqrs",
    "8": "tuv",
    "9": "wxyz",
}

def letter_combinations_of_a_phone_number(digits_str):
    result_str_arr = []
    if not digits_str:
        return result_str_arr
    assert "1" not in digits_str, "we dont proc 1"
    
    middle_state_container = []
    _get_letter_combination(result_str_arr, digits_str, index=0,
        middle_state_container=middle_state_container)
    return result_str_arr    

def _get_letter_combination(
        result_str_arr, pending_proc_digits_str, index, middle_state_container):
    """
    middle_state_container 中保存了
    此时从 pending_proc_digits_str[0...index-1] 翻译得到的一个字母字符串
    寻找和pending_proc_digits_str[index]匹配的字母,
    获得pending_proc_digits_str[0...index]翻译得到的解
    """
    if index == len(pending_proc_digits_str):
        # 当index等于数字字符串长度的时候说明一轮已经递归到底了,
        # 则当前的 中间状态保存器 middle_state_container 则为一个解
        # 此处需要深拷贝一下, 因为下方代码有个 `middle_state_container.pop(-1)`
        result_str_arr.append(copy.deepcopy(middle_state_container))
        return 
    # # 不处理1因为1对应的没字母
    # while pending_proc_digits_str[index] == "1":
    #     index += 1
    #     if index >= len(pending_proc_digits_str):
    #         return
    _cur_letters_str = digits_map[pending_proc_digits_str[index]]
    for _single_letter_str in _cur_letters_str:
        middle_state_container.append(_single_letter_str)
        _get_letter_combination(
            result_str_arr, pending_proc_digits_str, index+1,
            middle_state_container)
        middle_state_container.pop(-1)

组合问题合集

组合问题代码模板

和本文的lc77-经典组合问题基本一致.

lc77-经典组合问题

leetcode77题
给出两个整数n和k, 求出1…n中k个数字的所有组合
如n=4, k=2, 则结果为[ [1, 2], [1, 3], [1, 4], [2, 3], [2, 4], [3, 4] ]

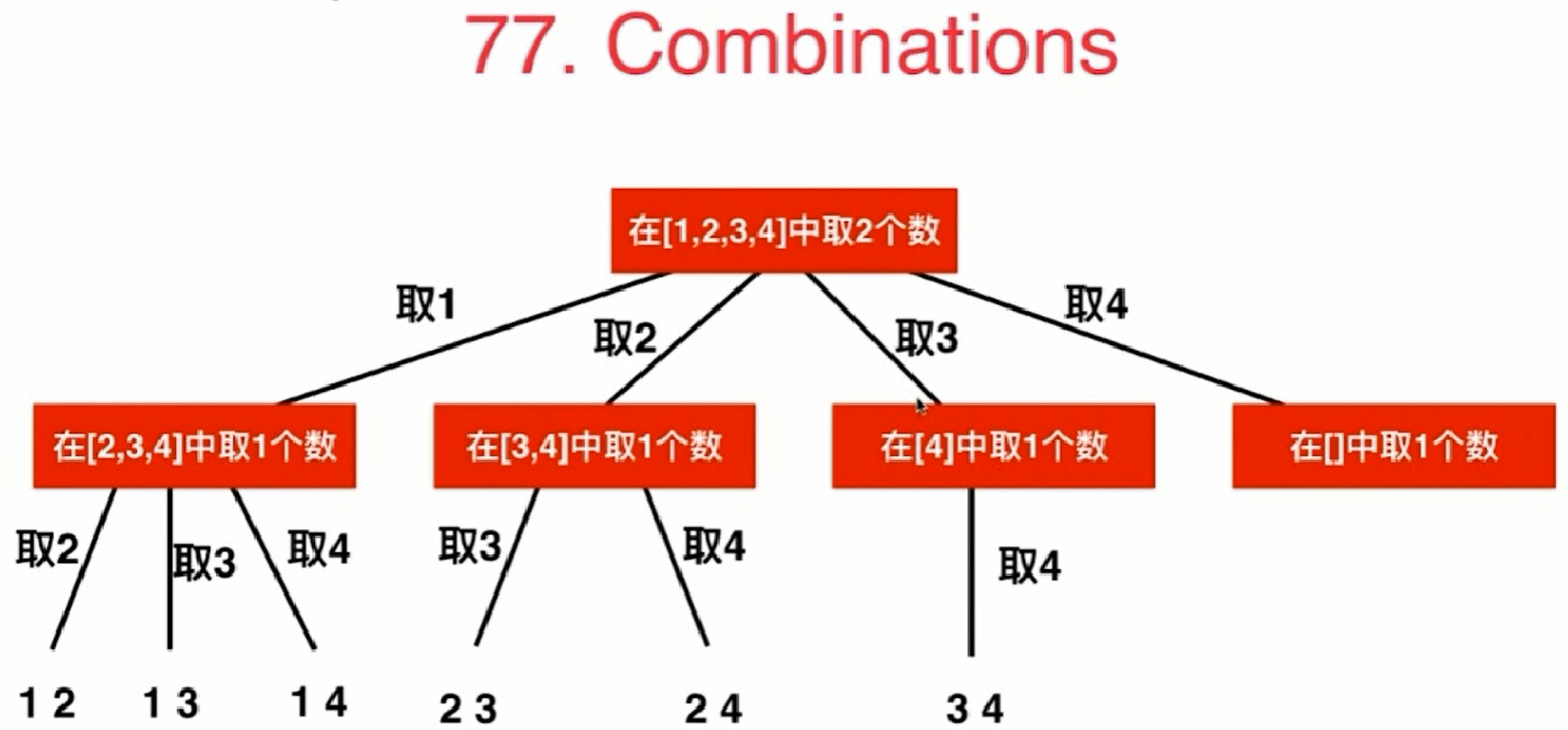
class Solution_lc77(object):
    def combine(self, n, k):
        """
        :type n: int
        :type k: int
        :rtype: List[List[int]]
        """
        result_arr = []
        if k <= 0 or k > n or n <= 0:
            return result_arr
        middle_state_container = []
        self._generate_combinations(result_arr, n, k, 1, middle_state_container)
        return result_arr
        
    def _generate_combinations(
            self, result_arr,
            pending_proc_n, pending_prco_k, start_num, middle_state_container):
        """
        求解C(n,k), 当前已经找到的组合存储在 middle_state_container 中,
        需要从start_num开始搜索新的元素
        可以看出跟排列问题的代码模板很像, 
        只有终止递归条件和for循环的start_num不太一样
        """
        if len(middle_state_container) == pending_prco_k:
            result_arr.append(copy.deepcopy(middle_state_container))
            return
        # 每次递归从start_num开始直到 pending_proc_n
        for _index in xrange(start_num, pending_proc_n+1):
            middle_state_container.append(_index)
            self._generate_combinations(
                result_arr, pending_proc_n, pending_prco_k,
                _index+1, middle_state_container)
            middle_state_container.pop(-1)

组合问题解决优化-剪枝

从上面的 组合问题解题思路 中可以看出其实是没有必要计算 “取4” 的操作的,
所以我们利用剪枝的思想, 把这部分优化掉, 代码如下:

def _generate_combinations_optimized(
        self, result_arr,
        pending_proc_n, pending_prco_k, start_num, middle_state_container):
    """
    求解C(n,k), 当前已经找到的组合存储在 middle_state_container 中,
    需要从start_num开始搜索新的元素
    可以看出跟排列问题的代码模板很像, 
    只有终止递归条件和for循环的start_num不太一样
    """
    if len(middle_state_container) == pending_prco_k:
        result_arr.append(copy.deepcopy(middle_state_container))
        return
-   # 每次递归从start_num开始直到 pending_proc_n
-   for _cur_num in xrange(start_num, pending_proc_n+1):
+   # 剪枝的思想, 
+   # 还有k - middle_state_container.size()个空位,
+   # 所以, [i...n] 中至少要有 k - middle_state_container.size() 个元素
+   # i最多为 n - (k - middle_state_container.size()) + 1
+   _cur_stop_num = pending_proc_n - (
+       pending_prco_k - middle_state_container.size()) + 1
+   # 每次递归从start_num开始直到 _cur_stop_num
+   for _cur_num in xrange(start_num, _cur_stop_num+1):
        middle_state_container.append(_cur_num)
        self._generate_combinations(
            result_arr, pending_proc_n, pending_prco_k,
            _cur_num+1, middle_state_container)
        middle_state_container.pop(-1)

lc39-组合总和

lc39

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。candidates 中的数字可以无限制重复被选取。说明：

• 所有数字（包括 target）都是正整数。
• 解集不能包含重复的组合。

示例 1：
输入：candidates = [2,3,6,7], target = 7,
所求解集为：

[
  [7],
  [2,2,3]
]

示例 2：
输入：candidates = [2,3,5], target = 8,
所求解集为：

[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

参考
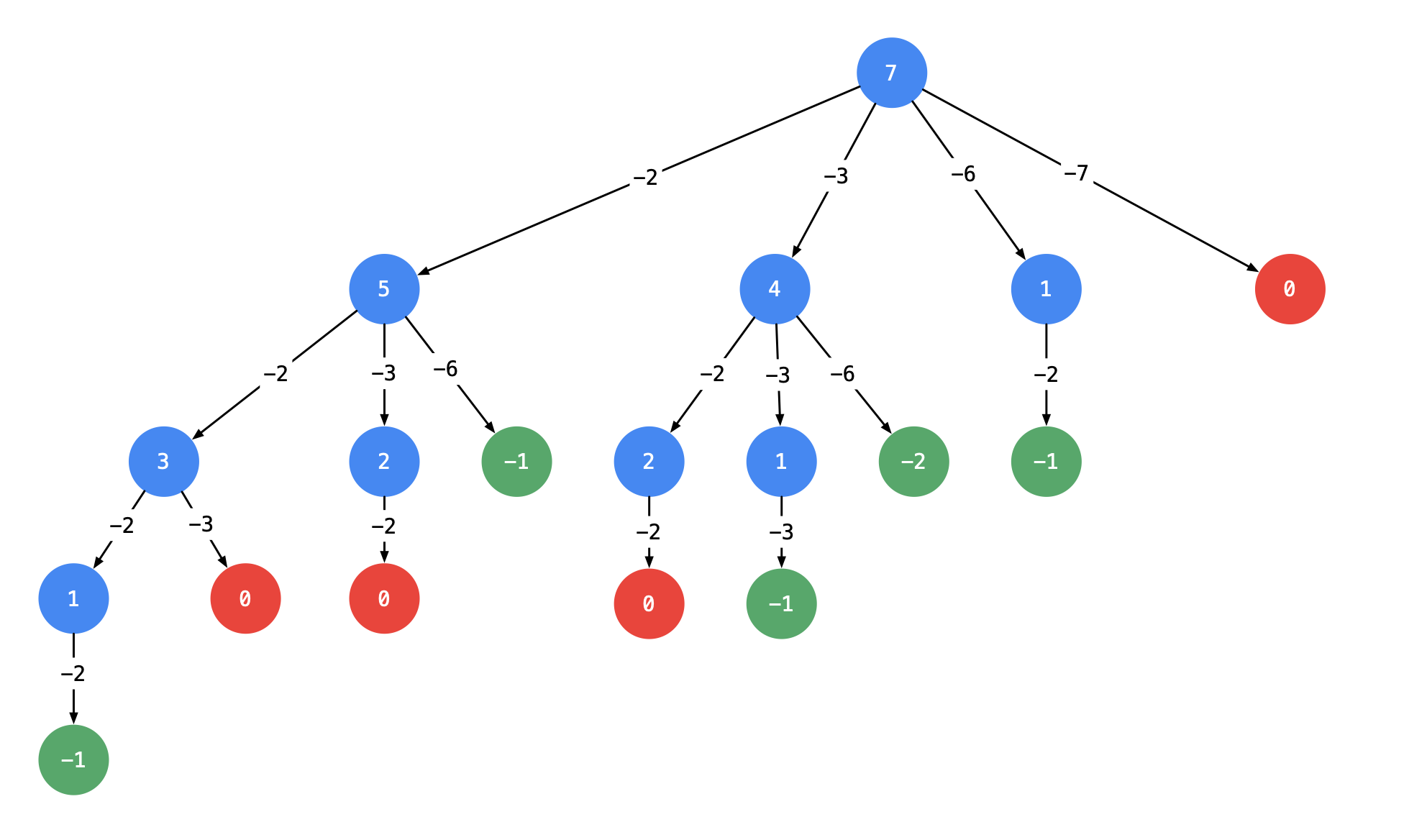
以输入：candidates = [2, 3, 6, 7], target = 7 为例
这棵树有 44 个叶子结点的值 00，对应的路径列表是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]]，而示例中给出的输出只有 [[7], [2, 2, 3]]。即：题目中要求每一个符合要求的解是 不计算顺序 的。下面我们分析为什么会产生重复。

针对具体例子分析重复路径产生的原因（难点）
友情提示：这一部分我的描述是晦涩难懂的，建议大家先自己观察出现重复的原因，进而思考如何解决。
产生重复的原因是：在每一个结点，做减法，展开分支的时候，由于题目中说 每一个元素可以重复使用，我们考虑了 所有的 候选数，因此出现了重复的列表。
一种简单的去重方案是借助哈希表的天然去重的功能，但实际操作一下，就会发现并没有那么容易。
可不可以在搜索的时候就去重呢？答案是可以的。遇到这一类相同元素不计算顺序的问题，我们在搜索的时候就需要 按某种顺序搜索。具体的做法是：每一次搜索的时候设置 下一轮搜索的起点 start_index, 请看下图。

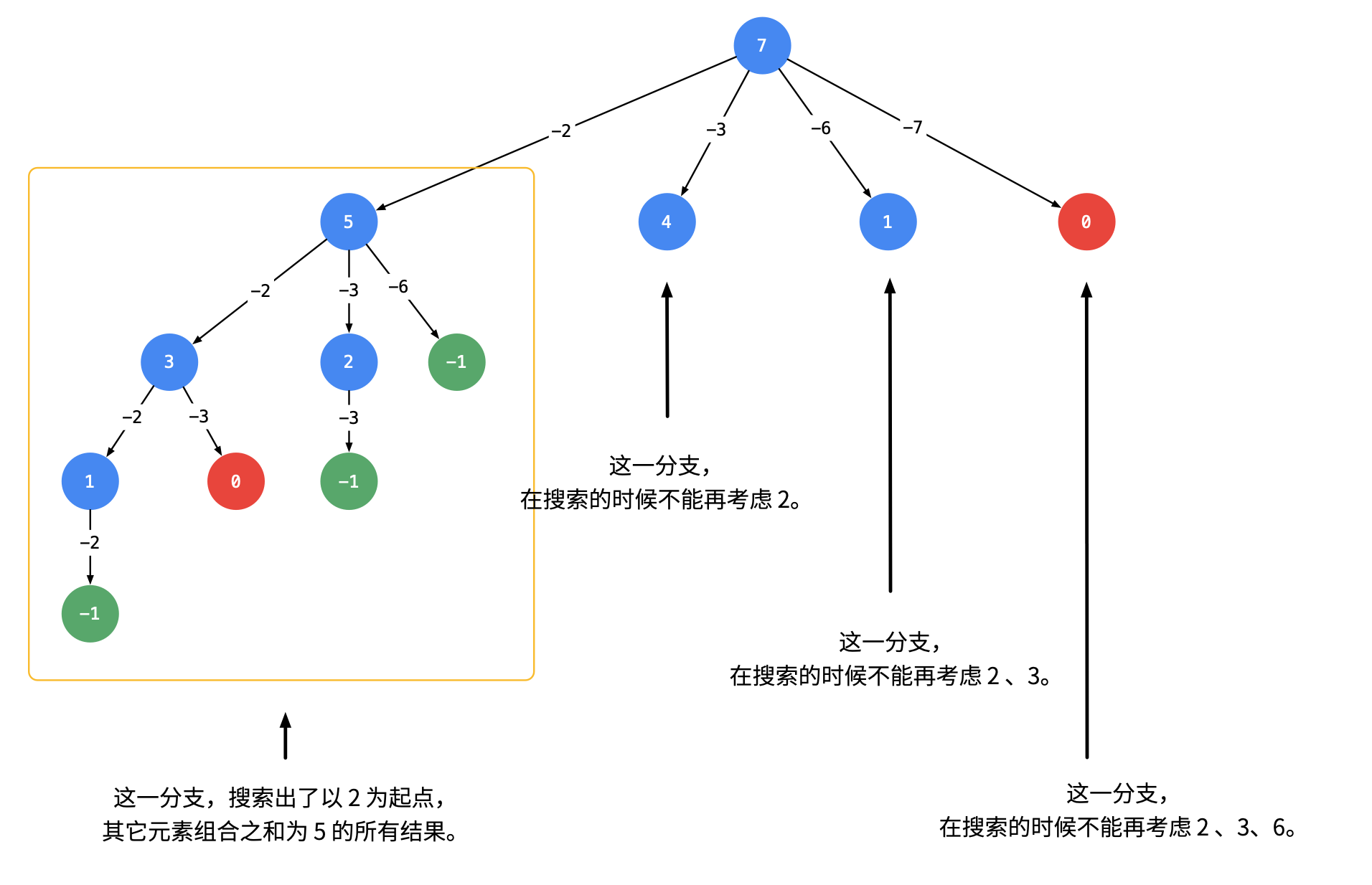
即：从每一层的第 22 个结点开始，都不能再搜索产生同一层结点已经使用过的 candidate 里的元素

class Solution_lc39(object):
    def combinationSum(self, candidates, target):
        """
        :type candidates: List[int]
        :type target: int
        :rtype: List[List[int]]
        """
        if not candidates:
            return []
        res_arr = []
        middle_state_arr = []
        self._generate_combinations(candidates, target, 0, res_arr, middle_state_arr)
        return res_arr

    def _generate_combinations(
            self, candidates_arr, cur_target_num, start_index, res_arr, middle_state_arr):
        if cur_target_num < 0:
            return
        if cur_target_num == 0:
            res_arr.append(copy.deepcopy(middle_state_arr))
            return
        # 这个cur_index是用来去除重复组合的
        for cur_index in range(start_index, len(candidates_arr)):
            middle_state_arr.append(candidates_arr[cur_index])
            cur_target_num -= candidates_arr[cur_index]
            self._generate_combinations(
                candidates_arr, cur_target_num,
                cur_index,
                res_arr, middle_state_arr)
            cur_target_num += candidates_arr[cur_index]
            middle_state_arr.pop(-1)

进阶-lc40-组合总和2

lc40 如果candidates 中的每个数字在每个组合中只能使用一次呢?
那应该改成:

for cur_index in range(start_index, len(candidates_arr)):
    middle_state_arr.append(candidates_arr[cur_index])
    cur_target_num -= candidates_arr[cur_index]
    self._generate_combinations(
        candidates_arr, cur_target_num,
-       cur_index,
+       cur_index+1,
        res_arr, middle_state_arr)
    cur_target_num += candidates_arr[cur_index]
    middle_state_arr.pop(-1)

多个数组抽个数总和

题目: 4 个数组，目标值 target，每个数组各找一个数，使得 4 个数和为 target，数组没有顺序，找到所有不重复的组合，要求时间复杂度 O(n^2)

class Solution_multi_arr_sum(object):
    # 题目: 4 个数组，目标值 target，每个数组各找一个数，使得 4 个数和为 target，
    # 数组没有顺序，找到所有不重复的组合，
    # 要求时间复杂度 O(n^2)
    def multi_arr_sum(self, nums_arrs, target_sum_num):
        if not nums_arrs:
            return []
        middle_arr = []
        res_arr = []
        self._generate_result(
            nums_arrs, target_sum_num, 0, res_arr, middle_arr)
        return res_arr
        
    def _generate_result(
            self, nums_arrs, target_sum_num,
            start_i_index,
            res_arr, middle_arr):
        if target_sum_num < 0:
            return
        if len(middle_arr) == len(nums_arrs):
            if target_sum_num == 0:
                res_arr.append(copy.deepcopy(middle_arr))
            return
        for i in range(start_i_index, len(nums_arrs)):
            for j in range(0, len(nums_arrs[i])):
                middle_arr.append(nums_arrs[i][j])
                self._generate_result(
                    nums_arrs, target_sum_num-nums_arrs[i][j],
                    i+1,
                    res_arr, middle_arr
                )
                middle_arr.pop(-1)

print "----------multi_arr_sum-------"  
print 'Solution_multi_arr_sum().multi_arr_sum([[1, 2], [3, 4], [5, 6, 9], [7, 8]], 18) :'
print Solution_multi_arr_sum().multi_arr_sum([[1, 2], [3, 4], [5, 6, 9], [7, 8]], 18)

打印结果:

----------multi_arr_sum-------
Solution_multi_arr_sum().multi_arr_sum([[1, 2], [3, 4], [5, 6, 9], [7, 8]], 18) :
[[1, 3, 6, 8], [1, 4, 5, 8], [1, 4, 6, 7], [2, 3, 5, 8], [2, 3, 6, 7], [2, 4, 5, 7]]

排序组合总结

什么时候使用 used 数组，什么时候使用 begin 变量
有些朋友可能会疑惑什么时候使用 used 数组，什么时候使用 begin 变量。这里为大家简单总结一下：

• 排列问题，讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为不同列表时），需要记录哪些数字已经使用过，此时用 used 数组；
• 组合问题，不讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为相同列表时），需要按照某种顺序搜索，此时使用 begin 变量。

注意：具体问题应该具体分析， 理解算法的设计思想 是至关重要的，请不要死记硬背。

岛屿数量-经典floodfill问题

lc200
给你一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，请你计算网格中岛屿的数量。
岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外，你可以假设该网格的四条边均被水包围。

示例 1：
输入：grid = [
[“1”,”1”,”1”,”1”,”0”],
[“1”,”1”,”0”,”1”,”0”],
[“1”,”1”,”0”,”0”,”0”],
[“0”,”0”,”0”,”0”,”0”]
]
输出：1
如下图则有1个岛屿: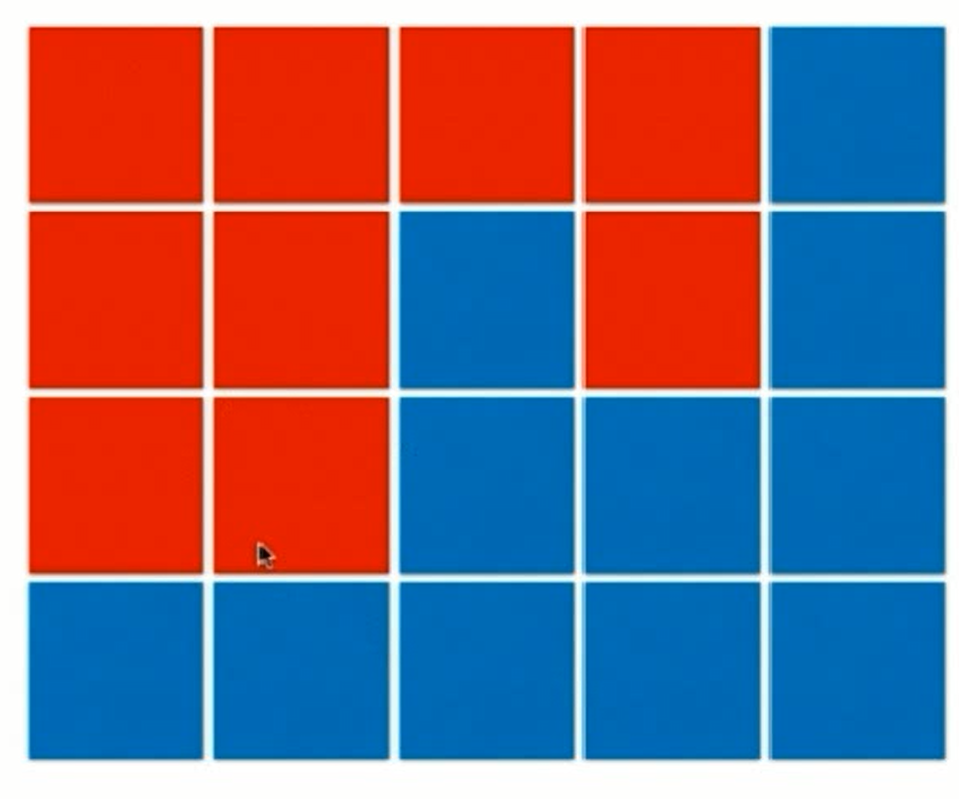

示例 2：
输入：grid = [
[“1”,”1”,”0”,”0”,”0”],
[“1”,”1”,”0”,”0”,”0”],
[“0”,”0”,”1”,”0”,”0”],
[“0”,”0”,”0”,”1”,”1”]
]
输出：3
如下图则有3个岛屿:

此题也可以用并查集来解, 见本文的岛屿数量-并查集实战
用dfs的解法代码如下:

class Solution_number_of_islands(object):

    def __init__(self):
        self._visited_pos_set = set()
        # 方便搜索点的时候往上下左右搜
        self._move_dir_arr = [(0, -1), (0, 1), (1, 0), [-1, 0]]

    def numIslands(self, grid):
        """
        :type grid: List[List[str]]
        :rtype: int
        """
        if not grid:
            return 0
        islands_cnt = 0
        for x in xrange(0, len(grid)):
            assert (type(grid[x]) is list), ("x = %d" % x)
            for y in xrange(0, len(grid[x])):
                if tuple([x, y]) in self._visited_pos_set:
                    continue
                if grid[x][y] != "1":
                    continue
                self._dfs_islands(grid, x, y)
                islands_cnt += 1  # 一次搜索完成就算有一个岛屿了
        return islands_cnt


    def _dfs_islands(self, grid, x, y):  # x是纵坐标, y是横坐标
        # print "x = %d" % x
        # print "y = %d" % y
        self._visited_pos_set.add(tuple([x, y]))
        # 上下左右四个方向搜索
        for _move_dir in self._move_dir_arr:
            _new_x = x + _move_dir[0]
            _new_y = y + _move_dir[1]
            # 如果超出地图边界了, 注意 x是纵坐标, y是横坐标
            if _new_x >= len(grid) or _new_x < 0 or \
                    _new_y >= len(grid[0]) or _new_y < 0:
                continue
            # 如果已经访问过了
            if tuple([_new_x, _new_y]) in self._visited_pos_set:
                continue
            if grid[_new_x][_new_y] != "1":
                continue
            self._dfs_islands(grid, _new_x, _new_y)

经典N皇后问题

… pending_fin

动态规划解题思路

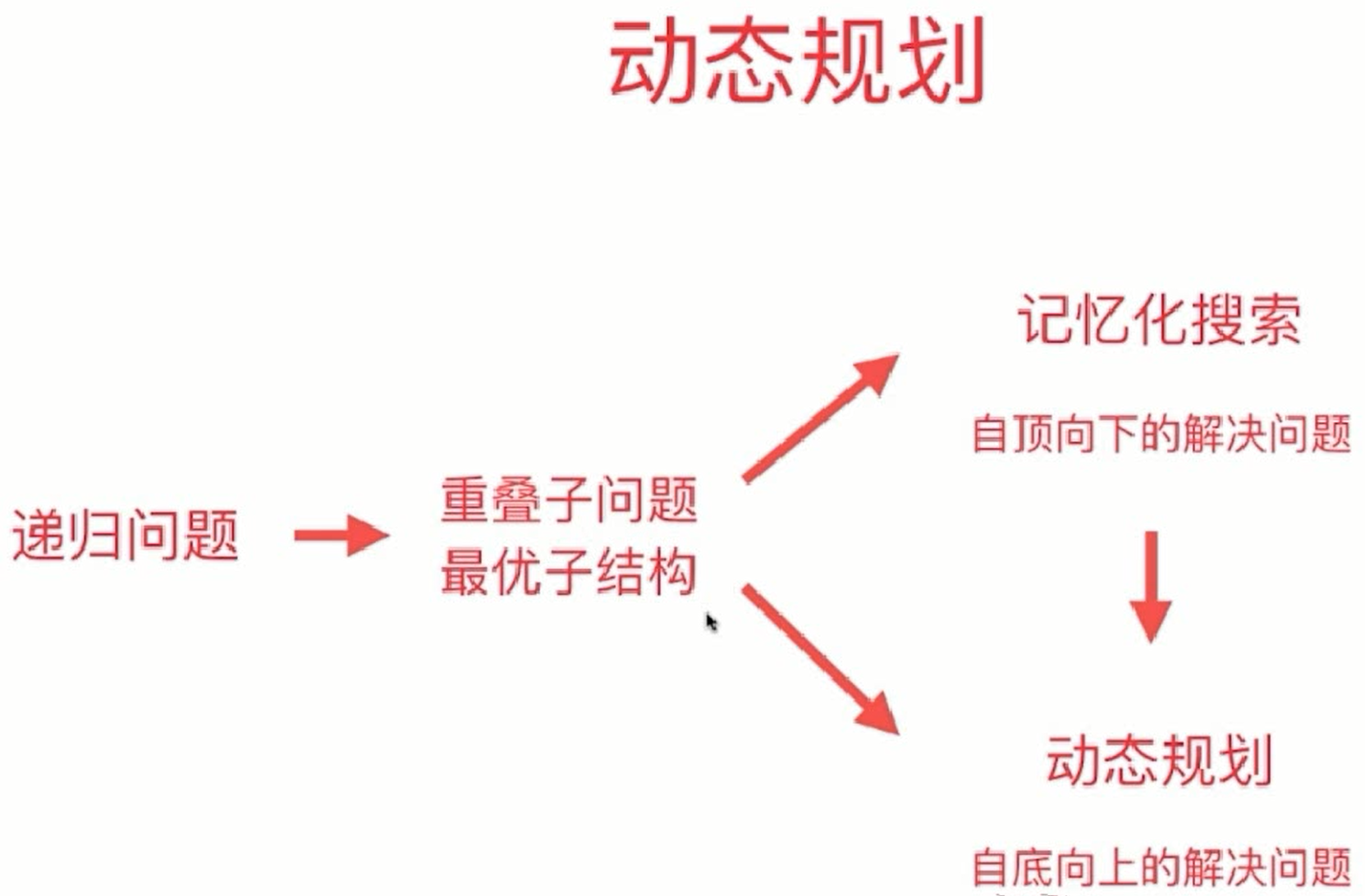
首先，动态规划的穷举有点特别，因为这类问题存在「重叠子问题」，如果暴力穷举的话效率会极其低下，所以需要「备忘录」或者「DP table」来优化穷举过程，避免不必要的计算。

而且，动态规划问题一定会具备「最优子结构」，才能通过子问题的最值得到原问题的最值。

另外，虽然动态规划的核心思想就是穷举求最值，但是问题可以千变万化，穷举所有可行解其实并不是一件容易的事，只有列出正确的「状态转移方程」才能正确地穷举。

以上提到的重叠子问题、最优子结构、状态转移方程就是动态规划三要素。具体什么意思等会会举例详解，但是在实际的算法问题中，写出状态转移方程是最困难的.

动态规划算法就是将待求解问题分解成若干子问题，先求解子问题并保存子问题的答案避免重复计算，然后从这些子问题的解得到原问题的解。而如何断定一个问题是否可以用动态规划来解决，就需要掌握动态规划的两个基本要素:

• 重叠子问题性质
• 最优子结构性质

重叠子问题性质

在用递归算法自顶向下解决一个问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。动态规划正是利用了这种子问题的重叠性质，对每个子问题只解一次，而后将其解保存到一个表格中，当再次需要解此子问题时，只是简单地用常数时间查看一下结果。
保存重叠子问题的解（也就是 fib(3)）有以下两种方式：

• DP table（自底向上）
• 备忘录memo方法又称记忆化搜索（自顶向下）

最优子结构性质

设计动态规划算法的第一步通常是要刻画最优解的结构。当问题的最优解包含了其子问题的最优解时，称该问题具有最优子结构性质 。问题的最优子结构性质提供了该问题可用动态规划求解的重要线索。

要符合 「最优⼦结构」，⼦问题间必须互相独⽴。啥叫相互独⽴？你肯定不想看数 学证明，我⽤⼀个直观的例⼦来讲解。

⽐如说，你的原问题是考出最⾼的总成绩，那么你的⼦问题就是要把语⽂考 到最⾼，数学考到最⾼…… 为了每门课考到最⾼，你要把每门课相应的选 择题分数拿到最⾼，填空题分数拿到最⾼…… 当然，最终就是你每门课都 是满分，这就是最⾼的总成绩。

得到了正确的结果：最⾼的总成绩就是总分。因为这个过程符合最优⼦结 构，“每门科⽬考到最⾼”这些⼦问题是互相独⽴，互不⼲扰的。

但是，如果加⼀个条件：你的语⽂成绩和数学成绩会互相制约，此消彼⻓。 这样的话，显然你能考到的最⾼总成绩就达不到总分了，按刚才那个思路就 会得到错误的结果。因为⼦问题并不独⽴，语⽂数学成绩⽆法同时最优，所 以最优⼦结构被破坏。

解决动态规划问题步骤

动态规划（Dynamic Programming，DP）是在多项式时间解决特定类型问题的一套方法论，且远远快于指数级别的蛮力法.
解决动态规划问题三步法：

1. 辨别是不是一个动态规划问题；
2. 建立状态之间的关系, 构造状态转移方程
   1. 明确 base case
   2. 明确「状态」也就是原问题和子问题中会变化的变量。
   3. 明确「选择」, 也就是导致「状态」产生变化的行为。
   4. 定义 dp 数组 / 函数的含义
3. 代码实现方式, 以下两种方式选其一:
   • 为状态添加备忘录memo自顶向下用记忆化搜索的递归方式来写
   • 用DP Table的动规方式来写

按上面的套路走，最后的结果就可以套这个框架：

dp[0][0][...] = base
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)

第一步-断定是否为动规问题

一般情况下，需要求最优解的问题（最短路径问题，最长公共子序列，最大字段和等等，出现 最 字你就留意），在一定条件下对排列进行计数的计数问题（丑数问题）或某些概率问题都可以考虑用动态规划来解决。

所有的动态规划问题都满足重叠子问题性质，大多数经典的动态规划问题还满足最优子结构性质，当我们从一个给定的问题中发现了这些特性，就可以确定其可以用动态规划解决。

第二步-构造状态转移方程

其步骤为:

1. 明确 base case
2. 明确「状态」也就是原问题和子问题中会变化的变量。
3. 明确「选择」, 也就是导致「状态」产生变化的行为。
4. 定义 dp 数组 / 函数的含义

DP 问题最重要的就是确定所有的状态和状态与状态之间的转移方程。确定状态转移方程是动态规划最难的部分，但也是最基础的，必须非常谨慎地选择状态，因为状态转移方程的确定取决于你对问题状态定义的选择。那么，状态到底是个什么鬼呢？
「状态」 可以视为一组可以唯一标识给定问题中某个子问题解的参数，这组参数应尽可能的小，以减少状态空间的大小。

• 比如斐波那契数中，0 , 1, …, n 就可以视为参数，而通过这些参数定义出的 DP[0]，DP[1]，DP[2]，…，DP[n] 就是状态，而状态与状态之间的转移方程就是 DP(n) = DP(n-1) + DP(n-2) 。
• 再比如，经典的背包问题（Knapsack problem）中，状态通过 index 和 weight 两个参数来定义，即 DP[index][weight] 。DP[index][weight] 则表示当前从 0 到 index 的物品装入背包中可以获得的最大重量。因此，参数 index 和 weight 可以唯一确定背包问题的一个子问题的解。

所以，当确定给定的问题之后，首当其冲的就是确定问题的状态。动态规划算法就是将待求解问题分解成若干子问题，先求解子问题并保存子问题的答案避免重复计算，然后从这些子问题的解得到原问题的解。既然确定了一个一个的子问题的状态，接下来就是确定前一个状态到当前状态的转移关系式，也称状态转移方程。

构造状态转移方程是 DP 问题最难的部分，需要足够敏锐的直觉和观察力，而这两者都是要通过大量的练习来获得。我们用一个简单的问题来理解这个步骤: 凑零钱

第三步-用备忘录或者DP表来代码实现

这个可以说是动态规划最简单的部分，我们仅需要存储子状态的解，以便下次使用子状态时直接查表从内存中获得。代码书写方式以下二者选其一:

• 为状态添加备忘录memo自顶向下用记忆化搜索的递归方式来写
• 用DP Table的动规方式来写.

备忘录memo VS DP表:

• 状态：DP Table 状态转移关系较难确定，备忘录状态转移关系较易确定。你可以理解为自顶向下推导较为容易，自底向上推导较难。比如 DP[n] = DP[n - 1] + DP[n - 3] + DP[n-5] 的确定。
• 代码：当约束条件较多的情况下，DP Table 较为复杂；备忘录代码相对容易实现和简单，仅需对递归代码进行改造。
• 效率：动态规划（DP Table）较快，我们可以直接从表中获取子状态的解；备忘录由于大量的递归调用和返回状态操作，速度较慢。
• 子问题的解：当所有的子问题的解都至少要被解一遍，自底向上的动态规划算法通常比自顶向下的备忘录方法快常数量级；当求解的问题的子问题空间中的部分子问题不需要计算，仅需求解部分子问题就可以解决原问题，此时备忘录方法要优于动态规划，因为备忘录自顶向下仅存储与原问题求解相关的子问题的解。
• 表空间：DP Table 依次填充所有子状态的解；而备忘录不必填充所有子问题的解，而是按需填充。

至于两个该如何选择，我想你的心中也有数了，建议按照解动态规划的四步骤依次求解，至于第四步，你个人喜欢用 DP Table 就用 DP Table ，喜欢备忘录就用备忘录。

理解动态规划-讲解凑零钱1

lc322
先看下题目：给你 k 种面值的硬币，面值分别为 c1, c2 ... ck，每种硬币的数量无限，再给一个总金额 amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。算法的函数签名如下：

int coinChange(int[] coins, int amount);

比如说 k = 3，面值分别为 1，2，5，总金额 amount = 11。那么最少需要 3 枚硬币凑出，即 11 = 5 + 5 + 1。

你认为计算机应该如何解决这个问题？显然，就是把所有肯能的凑硬币方法都穷举出来，然后找找看最少需要多少枚硬币。

首先，这个问题是动态规划问题，因为它具有「最优子结构」的。

为什么说它符合最优子结构呢？比如你想求 amount = 11 时的最少硬币数（原问题），如果你知道凑出 amount = 10 的最少硬币数（子问题），你只需要把子问题的答案加一（再选一枚面值为 1 的硬币）就是原问题的答案。因为硬币的数量是没有限制的，所以子问题之间没有相互制约，是互相独立的。

分析状态转移

那么，既然知道了这是个动态规划问题，就要思考如何列出正确的状态转移方程？

1、确定 base case，这个很简单，显然目标金额 amount 为 0 时算法返回 0，因为不需要任何硬币就已经凑出目标金额了。

2、确定「状态」，也就是原问题和子问题中会变化的变量。由于硬币数量无限，硬币的面额也是题目给定的，只有目标金额会不断地向 base case 靠近，所以唯一的「状态」就是目标金额 amount。

3、确定「选择」，也就是导致「状态」产生变化的行为。目标金额为什么变化呢，因为你在选择硬币，你每选择一枚硬币，就相当于减少了目标金额。所以说所有硬币的面值，就是你的「选择」。

4、明确 dp 函数 / 数组的定义。我们这里讲的是自顶向下的解法，所以会有一个递归的 dp 函数，一般来说函数的参数就是状态转移中会变化的量，也就是上面说到的「状态」；函数的返回值就是题目要求我们计算的量。就本题来说，状态只有一个，即「目标金额」，题目要求我们计算凑出目标金额所需的最少硬币数量。所以我们可以这样定义 dp 函数：

dp(n) 的定义：输入一个目标金额 n，返回凑出目标金额 n 的最少硬币数量。

搞清楚上面这几个关键点，解法的伪码就可以写出来了：

def coinChange(coins: List[int], amount: int):
    def dp(n):
        for coin in coins:
            res = min(res, 1 + dp(n - coin))
        return res
    return dp(amount)

根据伪码，我们加上 base case 即可得到最终的答案。显然目标金额为 0 时，所需硬币数量为 0；当目标金额小于 0 时，无解，返回 -1：

暴力递归解法

def coinChange(coins: List[int], amount: int):
    def dp(n):
        if n == 0: return 0
        if n < 0: return -1
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            if subproblem == -1:
                continue
            res = min(res, 1 + subproblem)
        return res if res != float('INF') else -1
    return dp(amount)

至此，状态转移方程其实已经完成了，以上算法已经是暴力解法了，以上代码的数学形式就是状态转移方程：

dp[n] = min(dp[n-coin])+1, 当n >0
dp[n] = 0, 当n = 0;
dp[n] = -1, 当n < 0;

至此，这个问题其实就解决了，只不过需要消除一下重叠子问题

递归算法的时间复杂度分析：子问题总数 x 每个子问题的时间。

子问题总数为递归树节点个数，这个比较难看出来，是 O(n^k)，总之是指数级别的。每个子问题中含有一个 for 循环，复杂度为 O(k)。所以总时间复杂度为 O(k * n^k)，指数级别。

带备忘录的递归

只需要稍加修改，就可以通过备忘录消除子问题：

def coinChange(coins: List[int], amount: int):
    memo = dict()

    def dp(n):
        if n in memo:
            return memo[n]
        if n == 0: return 0
        if n < 0: return -1
        res = float('INF')
        for coin in coins:
            subproblem = dp(n - coin)
            if subproblem == -1:
                continue
            res = min(res, 1 + subproblem)
        memo[n] = res if res != float('INF') else -1
        return memo[n]
    return dp(amount)

不画图了，很显然「备忘录」大大减小了子问题数目，完全消除了子问题的冗余，所以子问题总数不会超过金额数 n，即子问题数目为 O(n)。处理一个子问题的时间不变，仍是 O(k)，所以总的时间复杂度是 O(kn)。

dp数组的迭代解法

参考

其实这个题还可以看成是一个恰好装满的完全背包问题, 见本文的这题的背包解法
我们采用自下而上的方式进行思考。仍定义 F(i) 为组成金额 i 所需最少的硬币数量，假设在计算 F(i) 之前，我们已经计算出 F(0)−F(i−1) 的答案。 则 F(i) 对应的转移方程应为
F(i) = min(F(i-Cj)) + 1 ​
其中代表Cj的是第 j 枚硬币的面值，即我们枚举最后一枚硬币面额是 Cj，那么需要从 i-Cj这个金额的状态 F(i-Cj)转移过来，再算上枚举的这枚硬币数量 1 的贡献，由于要硬币数量最少，所以 F(i) 为前面能转移过来的状态的最小值加上枚举的硬币数量 1 。

举个例子：假设 coins = [1, 2, 5], amount = 11
则，当 i==0 时无法用硬币组成，为 0 。当 i<0 时，忽略 F(i)

F(i)	最小硬币数量
F(0)	0 //金额为0不能由硬币组成
F(1)	1 //F(1)=min(F(1-1),F(1-2),F(1-5))+1=1
F(2)	1 //F(2)=min(F(2-1),F(2-2),F(2-5))+1=1
F(3)	2 //F(3)=min(F(3-1),F(3-2),F(3-5))+1=2
F(4)	2 //F(4)=min(F(4-1),F(4-2),F(4-5))+1=2
…	…
F(11)	3 //F(11)=min(F(11-1),F(11-2),F(11-5))+1=3

我们可以看到问题的答案是通过子问题的最优解得到的。

自底向上使用 dp table 来消除重叠子问题，关于「状态」「选择」和 base case 与之前没有区别，dp 数组的定义和刚才 dp 函数类似，也是把「状态」，也就是目标金额作为变量。不过 dp 函数体现在函数参数，而 dp 数组体现在数组索引：

dp数组的定义：当目标金额为i时，至少需要dp[i]枚硬币凑出。

根据我们文章开头给出的动态规划代码框架可以写出如下解法：

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1)
        dp[0] = 0
        
        for coin in coins:
            for x in range(coin, amount + 1):
                dp[x] = min(dp[x], dp[x - coin] + 1)
        return dp[amount] if dp[amount] != float('inf') else -1

动态规划各种题型

背包问题系列

0-1背包问题

注意: 「0-1 背包」问题是一类非常重要的动态规划问题
这个题目中的物品不可以分割，要么装进包里，要么不装，不能说切成两块装一半。这也许就是 0-1 背包这个名词的来历。

最基本的背包问题就是 01 背包问题（01 knapsack problem）：一共有 N 件物品，第 i（i 从 1 开始）件物品的重量为 w[i]，价值为 v[i]。在总重量不超过背包承载上限 W 的情况下，能够装入背包的最大价值是多少？

如果采用暴力穷举的方式，每件物品都存在装入和不装入两种情况，所以总的时间复杂度是 O(2^N)，这是不可接受的。而使用动态规划可以将复杂度降至 O(NW)。我们的目标是书包内物品的总价值，而变量是物品和书包的限重，所以我们可定义状态 dp:

dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W

那么我们可以将 dp[0][0…W] 初始化为 0，表示将前 0 个物品（即没有物品）装入书包的最大价值为 0。那么当 i > 0 时dp[i][j]有两种情况：

• 不装入第 i 件物品，即dp[i−1][j]；
• 装入第 i 件物品（前提是能装下），即dp[i−1][j−w[i-1]] + v[i-1]

为什么是i-1

注意上方的w[i-1]和v[i-1], 为什么是i-1呢?
因为我们对dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值, 则i=0其实表示的是前0个物品并不是第0个物品, 所以实际对应weight数组和value数组的index应该为i-1

即状态转移方程为

dp[i][j] = max(
    dp[i−1][j],
    dp[i−1][j−w[i-1]+v[i-1])  # j >= w[i-1]

所求的结果为dp[n][capacity]

根据状态转移方程得出以下动规代码:

def knapsack_dp(self, capacity, weight_arr, value_arr):
    if capacity == 0:
        return 0
    assert(len(weight_arr) == len(value_arr))
    n = len(weight_arr)
    # dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W
    # 那么我们可以将dp[0][0...W]初始化为0，
    # 表示将前0个物品（即没有物品）装入书包的最大价值为0。
    # 那么当 i > 0 时dp[i][j]有两种情况：
    # - 不装入第i件物品，即dp[i−1][j]；
    # - 装入第i件物品（前提是能装下），即dp[i−1][j−w[i-1]] + v[i-1]。
    # 因为我们对dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值
    # 则i=0其实表示的是0个物品,
    # 所以实际对应weight数组和value数组的index应该为i-1
    #
    # 即状态转移方程为
    # dp[i][j] = max(dp[i−1][j], dp[i−1][j−w[i-1]]+v[i-1]) // j >= w[i-1]
    # 所求为dp[n][capacity]
    dp = [[0 for _ in xrange(capacity+1)] for _ in xrange(n+1)]
    # 动规是从底向上嘛, 先构建dp[0]的东西
    for k in xrange(capacity+1):
        # 因为我们对dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值
        # 则i=0其实表示的是0个物品, 所以 = 0
        dp[0][k] = 0

    for i in xrange(1, n+1):
        for j in xrange(capacity+1):
            # 因为我们对dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值
            # 则i=0其实表示的是0个物品,
            # 所以实际对应weight数组和value数组的index应该为i-1
            pack_args_index = i - 1
            if j - weight_arr[pack_args_index] < 0:
                dp[i][j] = dp[i-1][j]
            else:
                dp[i][j] = max(
                    dp[i-1][j],
                    value_arr[pack_args_index] + dp[i-1][j-weight_arr[pack_args_index]]
                )
    return dp[n][capacity]

完全背包问题

完全背包（unbounded knapsack problem）与 01 背包不同就是每种物品可以有无限多个：一共有 N 种物品，每种物品有无限多个，第 i（i 从 1 开始）种物品的重量为 w[i]，价值为 v[i]。在总重量不超过背包承载上限 W 的情况下，能够装入背包的最大价值是多少？

我们的目标和变量和 01 背包没有区别，所以我们可定义与 01 背包问题几乎完全相同的状态 dp:

dp[i][j]表示将前i种物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W

为什么完全背包是i而不是i-1

我们注意!!!!! 完全背包问题的i指的是前i种, 而不是前i个, 这一点跟0-1背包是不同的, 0-1背包的i指的是前i个
初始状态也是一样的，我们将 dp[0][0…W] 初始化为 0，表示将前 0 种物品（即没有物品）装入书包的最大价值为 0。那么当 i > 0 时, 准备要放入第i种的某一个物品item_i_1时(注意, 是第i种的某一个, 第i种还可以有其他同种物品item_i_2, item_i_3…), 也有两种情况：

• 不装入第 i 种的当前这个物品item_i_1时，那只会有前i-1种商品了, 即dp[i−1][j]
• 装入第 i 种物品当前这个物品item_i_1时，此时和 0-1 背包不太一样，因为每种物品有无限个（但注意书包限重是有限的），所以此时不应该转移到dp[i−1][j−w[i-1]]而应该转移到dp[i][j−w[i-1]]，因为item_i_1是第i种物品的某一个物品, 所以应该放到dp[i]这个第i种物品的坑位里, 即装入item_i_1了之后还可以装入item_i_2, item_i_3…所以此时为: dp[i][j−w[i-1]] + v[i-1]

为什么是i-1

所以状态转移方程为

dp[i][j] = max(
    dp[i−1][j],
    dp[i][j−w[i-1]]+v[i-1])  # j >= w[i-1]

可以看出这个状态转移方程与 0-1 背包问题唯一不同就是i的含义不同导致的 max 第二项不是 dp[i-1] 而是 dp[i]。

背包问题的其他形式

• 恰好装满
  实战题目:
  • lc416-分割等和子集-恰好装满0-1背包问题
  • lc322-凑金币1-恰好装满的完全背包问题

• 求方案总数
  除了在给定每个物品的价值后求可得到的最大价值外，还有一类问题是问装满背包或将背包装至某一指定容量的方案总数。对于这类问题，需要将状态转移方程中的 max 改成 sum ，大体思路是不变的。例如若每件物品均是完全背包中的物品，转移方程即为

  dp[i][j] = sum(dp[i−1][j], dp[i][j−w[i-1]])  # j >= w[i-1]

  实战题目: lc518-凑零钱2-恰好装满完全背包问题
  为什么是i-1
  为什么完全背包是i而不是i-1

• 二维背包
  前面讨论的背包容量都是一个量：重量。二维背包问题是指每个背包有两个限制条件（比如重量和体积限制），选择物品必须要满足这两个条件。此类问题的解法和一维背包问题不同就是dp数组要多开一维，其他和一维背包完全一样
  实战题目:
  • lc474-一和零-二维0-1背包

背包问题实战

分割等和子集-恰好装满0-1背包问题

leetcode416题
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
示例 1:
输入: [1, 5, 11, 5]
输出: true
解释: 数组可以分割成 [1, 5, 5] 和 [11].
示例 2:
输入: [1, 2, 3, 5]
输出: false
解释: 数组不能分割成两个元素和相等的子集.

参考
这其实是一个恰好装满0-1背包问题, 我们只要拿一定的数字填满所有数字和sum的一半, 剩余的数字一定等于sum/2, 则这个问题其实还是个背包问题, 只不过我们需要用一定的数字把这个背包填满, 对于第i个物品, 有两种情况:

• 我们用i-1就填满了背包, 则第i个就不需要用了
• 我们用了第i个才填满

状态定义：
dp[i][j]表示对于容量为 j 的背包，若只是用前 i 个物品(前0个则表示没有物品)，每个数只能用一次，使得这些数的和恰好等于 j .
(比如说，如果dp[4][9] = true，其含义为：对于容量为 9 的背包，若只是用前 4 个物品，可以有一种方法把背包恰好装满。)。

状态转移方程：很多时候，状态转移方程思考的角度是「分类讨论」，对于「0-1 背包问题」而言就是「当前考虑到的数字选与不选」。

• 不选择 nums[i]，则看前i-1个元素的是否能能和为j, 即 dp[i-1][j]
• 选择 nums[i]，看前i-1个元素的是否能能和为j-nums[i-1], 即dp[i-1][j- nums[i-1]

为什么是i-1
则状态转移方程：
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i-1]] // j >= nums[i-1]

一般写出状态转移方程以后，就需要考虑初始化条件。

• 初始化：
  • dp[0][0] = True # 前0个则表示没有物品, 可以充满容量为0的背包
  • dp[0][c] = False # 前0个则表示没有物品, 是不可能充满容量c大于0的背包的
• 输出：dp[len][target]，这里 len 表示nums数组的长度，target 是数组的元素之和（必须是偶数）的一半。

则代码如下:

def canPartition(self, nums):
    """
    :type nums: List[int]
    :rtype: bool
    动规解法
    """
    # 特判：如果是奇数，就不符合要求
    if not nums or len(nums) < 2 or sum(nums) % 2 != 0:
        return False
    _bag_capcity = sum(nums) / 2
    n = len(nums)
    # 状态定义：
    # dp[i][j]表示对于容量为 j 的背包，若只是用前 i 个物品(前0个则表示没有物品)，
    # 每个数只能用一次，使得这些数的和恰好等于 j  .
    # (比如说，如果dp[4][9] = true，其含义为：对于容量为 9 的背包，若只是用前 4 个物品，可以有一种方法把背包恰好装满。)。
    # 状态转移方程：很多时候，状态转移方程思考的角度是「分类讨论」，对于「0-1 背包问题」而言就是「当前考虑到的数字选与不选」。
    # - 不选择 nums[i]，则看前i-1个元素的是否能能和为j, 即 `dp[i-1][j]`
    # - 选择 nums[i]，看前i-1个元素的是否能能和为`j-nums[i-1]`, 即`dp[i-1][j- nums[i-1]`
    # **注意上方的`nums[i-1]`, 为什么是i-1呢?**
    # 因为我们对dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值, 则i=0其实表示的是0个物品,
    # 所以实际对应nums数组的index应该为`i-1`
    # 则状态转移方程：
    # dp[i][j] = dp[i - 1][j] or dp[i - 1][j - nums[i-1]]  // j >= nums[i-1]
    dp = [[False for _ in range(_bag_capcity+1)] for _ in range(n+1)]

    dp[0][0] = True  # 前0个则表示没有物品, 可以充满容量为0的背包
    for c in range(1, _bag_capcity+1):
        dp[0][c] = False # 前0个则表示没有物品, 是不可能充满容量大于0的背包的
        
    for i in range(1, n+1):
        for j in range(_bag_capcity+1):
            if j - nums[i-1] < 0:
                dp[i][j] = dp[i-1][j]
            else:
                dp[i][j] = dp[i-1][j] or dp[i-1][j-nums[i-1]]
    return dp[n][_bag_capcity]

凑金币1-恰好装满的完全背包问题

lc322
先看下题目：给你 k 种面值的硬币，面值分别为 c1, c2 ... ck，每种硬币的数量无限，再给一个总金额 amount，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，算法返回 -1 。算法的函数签名如下：

int coinChange(int[] coins, int amount);

比如说 k = 3，面值分别为 1，2，5，总金额 amount = 11。那么最少需要 3 枚硬币凑出，即 11 = 5 + 5 + 1。

如果我们将每种硬币看作是每种物品，面值金额看成是物品的重量，总金额是背包的总容量, 因为硬币无限, 这样此题就是是一个恰好装满的完全背包问题了。不过这里不是求最多装入多少价值而是求最少装满背包的数目，所以我们只需要将完全背包的转态转移方程中稍微改改即可:

• dp[i][j]定义为: 用前i种硬币可以抽一些硬币出来装满容量为j的背包的最少硬币数量
• 状态转移方程为: d[i][j] = min(dp[i-1][j], dp[i][j-coins[i-1]]+1)

为什么是i-1
为什么完全背包是i而不是i-1

def coinChange(self, coins, amount):
    """
    :type coins: List[int]
    :type amount: int
    :rtype: int
    """
    assert(coins)
    # 用背包的思路
    if amount == 0:
        return 0
    n = len(coins)
    # 如果我们将每种硬币看作是每种物品，面值金额看成是物品的重量，总金额是背包的总容量, 因为硬币无限, 这样此题就是是一个恰好装满的完全背包问题.了。不过这里不是求最多装入多少价值而是求最少装满背包的数目，所以我们只需要将[完全背包](#完全背包问题)的转态转移方程中稍微改改即可:  
    # - dp[i][j]定义为: 用前i种硬币可以抽一些硬币出来装满容量为j的背包的最少硬币数量
    # - 状态转移方程为: `d[i][j] = min(dp[i-1][j], dp[i][j-coins[i-1]])`

    # 因为之后要取min操作, 所以这里初始化为无穷大`float("inf")`
    dp = [ [ float("inf") for _ in range(amount+1) ] for _ in range(n+1) ]
    for k in range(n+1):
        dp[k][0] = 0  # 充满容量为0的背包, 最少的硬币个数为0
    for i in range(n+1):
        for j in range(amount+1):
            if j - coins[i-1] < 0:
                dp[i][j] = dp[i-1][j]
            else:
                dp[i][j] = min(
                    dp[i-1][j],
                    dp[i][j-coins[i-1]] + 1
                )
    return dp[n][amount] if dp[n][amount] != float("inf") else -1

凑零钱2-恰好装满完全背包问题

lc518
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
示例 2:
输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。
示例 3:
输入: amount = 10, coins = [10]
输出: 1

我们可以把这个问题转化为背包问题的描述形式：
有一个背包，最大容量为amount，有一系列物品coins，每种物品的重量为coins[i]，每种物品的数量无限。请问有多少种方法，能够把背包恰好装满？
这个问题和我们前面讲过的两个0-1背包问题，有一个最大的区别就是，每种物品的数量是无限的，这也就是传说中的「完全背包问题」，没啥高大上的，无非就是状态转移方程有一点变化而已。这是一个恰好装满完全背包问题

1. 第一步要明确两点，「状态」和「选择」。
   这部分都是背包问题的老套路了，我还是啰嗦一下吧：状态有两个，就是「背包的容量」和「可选择的物品」，选择就是「装进背包」或者「不装进背包」。 明白了状态和选择，动态规划问题基本上就解决了

2. 第二步要明确dp数组的定义。
   首先看看刚才找到的「状态」，有两个，也就是说我们需要一个二维dp数组。
   dp[i][j]的定义如下：
   从前i种物品里选取若干件物品，当背包容量为j时，有dp[i][j]种方法可以装满背包。
   换句话说，翻译回我们题目的意思就是：
   若使用coins中的前i种硬币的面值，若想凑出金额j，有dp[i][j]种凑法。
   经过以上的定义，可以得到：
   base case 为

   • dp[0][..] = 0 因为如果不使用任何一种硬币，就无法凑出任何金额

   • dp[..][0] = 1 如果凑出的目标金额为 0，那么 “无为而治” (不用任何硬币)就是唯一的一种凑法。

     我们最终想得到的答案就是dp[N][amount]，其中N为coins数组的大小。

3. 第三步，根据「选择」，思考状态转移的逻辑。

   • 如果你不把这第i种的某个物品装入背包，也就是说你不使用coins[i]这种面值的硬币，那么凑出面额j的方法数dp[i][j]应该等于dp[i-1][j]，继承之前的结果。

   • 如果你把这第i种某个物品装入了背包，也就是说你使用coins[i]这种面值的硬币，那么dp[i][j]应该等于dp[i][j-coins[i-1]]。

     首先由于i是从 1 开始的，所以coins的索引是i-1时表示第i种硬币的面值。
     dp[i][j-coins[i-1]]也不难理解，如果你决定使用这种面值的硬币，那么就应该关注如何凑出金额j - coins[i-1]。
     比如说，你想用面值为 2 的硬币凑出金额 5，那么如果你知道了凑出金额 3 的方法，再加上一枚面额为 2 的硬币，不就可以凑出 5 了嘛。
     综上就是两种选择，而我们想求的dp[i][j]是「共有多少种凑法」，所以dp[i][j]的值应该是以上两种选择的结果之和
     则状态转移方程为: dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]]

def change(self, amount, coins):
    """
    :type amount: int
    :type coins: List[int]
    :rtype: int
    """ 
    n = len(coins)
    # dp[i][j]`的定义如下：  
    # 从前`i`种物品里选取若干件物品，当背包容量为`j`时，有`dp[i][j]`种方法可以装满背包。
    dp = [ [ 0 for _ in range(amount+1) ] for _ in range(n+1) ]
    for k in range(n+1):
        # 如果凑出的目标金额为 0，那么 “无为而治” (不用任何硬币)就是唯一的一种凑法。
        dp[k][0] = 1
    for i in range(1, n+1):
        for j in range(1, amount+1):
            if j - coins[i-1] < 0:
                dp[i][j] = dp[i-1][j]
            else:
                dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]]
    return dp[n][amount]

一和零-二维0-1背包

lc474
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小，该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。
示例 1：
输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,”0001”,”1”,”0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,”1”} 和 {“10”,”1”,”0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。
示例 2：
输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

pending_fini

股票利润最大系列

stock总结

我们先解决第四题, 然后:

• 第一题是只进行一次交易，相当于 k = 1；
• 第二题是不限交易次数，相当于 k = +infinity（正无穷）；
• 第三题是只进行 2 次交易，相当于 k = 2；
• 剩下两道也是不限交易次数，但是加了交易「冷冻期」和「手续费」的额外条件，其实就是第二题的变种，都很容易处理。

stock4-最通用的股票题

lc188, 我们先看股票的第4个题, 这个题最后代表性, 答案也最通用.

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。题中交易的含意是买入和卖出一支股票一次, 才称为一次交易
示例 1：
输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。
示例 2：
输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。
随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

• 参考1
• 参考2

注意: 题中交易的含意是买入和卖出一支股票一次, 才称为一次交易
但我们解题的时候可以把买入就当成一次交易会容易写代码一些,
当然也可以定义dp为买了再卖才算一次交易, 只是代码难写一些, 而且初始化状态难弄一些,

• dp[i][k][0]为前i天最多可以完成k次交易时手中 无股票时 的最大利润
• dp[i][k][1]为前i天最多可以完成k次交易时手中 有股票时 的最大利润

我们定义dp买入就算一次交易, 则:

# 前i天t次交易现在手上持有 = max(i-1天t次交易手上持有，i-1天t-1次交易手上不持有 - i天买入价格)
dp[i][t][1] = max(
    dp[i-1][t][1],
    # 为什么是`prices[i-1]`呢? 因为这里的i是第i天,
    # 根据我们的dp定义, 
    # 实际上第i=1天对应的是数组中的prices[0]的价格
    # 我们dp对交易的定义是买入就算, 这里买入一张股票, 得减去`prices[i-1]`
    # 所以我们这里才`t-1`, 好理解一些
    dp[i-1][t-1][0] - prices[i-1]
)
# 前i天t次交易现在手上不持有 = max(i-1天t次交易手上不持有，i-1天t次交易手上持有 + i天卖出价格prices)
dp[i][t][0] = max(
    dp[i-1][t][0],
    dp[i-1][t][1] + prices[i-1]
)

• dp[0][t][0] 前0天(即还没开始之意)t次交易，手上不持有：可能的 0
• dp[0][t][1] 前0天(即还没开始之意)t次交易，手上持有：不可能（前0天(即还没开始之意)没有股票，所以无法买入持有;持有说明至少进行了一次买入，买入就交易，因此这里不可能【不可能意思就是不能从这里转移】
• dp[i][0][0] 前i天0次交易，手上不持有：0
• dp[i][0][1] 前i天0次交易，手上持有：不可能（不交易手上不可能持有）

注意看下方代码的注释:

class Solution_stock(object):
    def stock4_maxProfit(self, k, prices):
        """
        :type k: int
        :type prices: List[int]
        :rtype: int
        """
        if not prices or not k:
            return 0
        n = len(prices)
        # 注意: 题中交易的含意是买入和卖出一支股票一次, 才称为一次交易
        # 但我们解题的时候可以把买入就当成一次交易会容易写代码一些,
        # 当然也可以定义dp为买了再卖才算一次交易, 只是代码难写一些, 而且
        # 初始化状态难弄一些
        # dp[i][k][0]为前i天最多可以完成k次交易时手中 无股票时 的最大利润
        # dp[i][k][1]为前i天最多可以完成k次交易时手中 有股票时 的最大利润
        # 为什么下方要初始化为`n+1`呢? 因为我们要求的是第n天最多可以完成k次交易时手中无股票时的最大利润,
        # 而不是第n-1天, 注意我们下方说的第0天并不是数组意义的第1天.
        # 读者可能问为什么不是 dp[n - 1][K][1]？
        # 因为 [1] 代表手上还持有股票，[0] 表示手上的股票已经卖出去了，
        # 很显然后者得到的利润一定大于前者。
        dp = [ [ [ 0 for _ in range(2) ]  for _ in range(k+1) ] for _ in range(n+1) ]
        
        for j in range(n+1):
            dp[j][0][0] = 0  # 前j天0次交易，手上不持有, 故为0
            # 前j天0次交易，手上持有股票, 这是不可能的, 
            # 我们dp对交易的定义是买入就算, 0次交易都没买入股票, 不可能持有股票
            # 所以我们用负无穷来表示, 因为之后我们用max来取值,
            # 如果这里不这样初始化，而是初始化为0，那么我t次交易的无法去做max,
            # max它会取这个0,而不会去取那些负值
            dp[j][0][1] = float("-inf")
            for t in range(k+1):
                # 前0天t次交易，手上持有股票, 这里所说的前0天不是数组的第1天,
                # 前0天是一个不存在的日子, 所以这是不可能的, 
                # 所以我们用负无穷来表示, 因为之后我们用max来取值,
                # 如果这里不这样初始化，而是初始化为0，那么我t次交易的无法去做max,
                # max它会取这个0,而不会去取那些负值
                dp[0][t][1] = float("-inf")
                dp[0][t][0] = 0
        for i in range(1, n+1):
            for t in range(1, k+1):
                # i天t次交易现在手上持有 = max(i-1天t次交易手上持有，i-1天t-1次交易手上不持有 - i天买入价格)
                dp[i][t][1] = max(
                    dp[i-1][t][1],
                    # 为什么是`prices[i-1]`呢? 因为这里的i是第i天,
                    # 根据我们的dp定义, 
                    # 实际上第i=1天对应的是数组中的prices[0]的价格
                    # 我们dp对交易的定义是买入就算, 这里买入一张股票, 得减去`prices[i-1]`
                    # 所以我们这里才`t-1`, 好理解一些
                    dp[i-1][t-1][0] - prices[i-1]
                )
                # i天t次交易现在手上不持有 = max(i-1天t次交易手上不持有，i-1天t次交易手上持有 + i天卖出价格prices)
                dp[i][t][0] = max(
                    dp[i-1][t][0],
                    dp[i-1][t][1] + prices[i-1]
                )

        return dp[n][k][0]

stock1

lc121
k=1

解法: 直接调用stock4的代码, 把k设置为1即可

stock2

lc122
k=无穷大

解法: 如果 k 为正无穷，那么就可以认为 k 和 k - 1 是一样的, k的约束已经没有作用了。所以dp数组可以去掉k这个维度.
忽略下方注释中的t, 则:

# i天t次交易现在手上持有 = max(i-1天t次交易手上持有，i-1天t-1次交易手上不持有 - i天买入价格)
dp[i][1] = max(
    dp[i-1][1],
    # 为什么是`prices[i-1]`呢? 因为这里的i是第i天,
    # 根据我们的dp定义, 
    # 实际上第i=1天对应的是数组中的prices[0]的价格
    # 我们dp对交易的定义是买入就算, 这里买入一张股票, 得减去`prices[i-1]`
    # 所以我们这里才`t-1`, 好理解一些
    dp[i-1][0] - prices[i-1]
)
# i天t次交易现在手上不持有 = max(i-1天t次交易手上不持有，i-1天t次交易手上持有 + i天卖出价格prices)
dp[i][0] = max(
    dp[i-1][0],
    dp[i-1][1] + prices[i-1]
)

stock3

lc123
k=2

解法: 直接调用stock4的代码, 把k设置为2即可

stock5

lc714

给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格 。​
设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

• 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
• 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。
  示例:
  输入: [1,2,3,0,2]
  输出: 3
  解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

题目特点:

• 可无限次交易, 则k还是无穷大, 那么就可以认为 k 和 k - 1 是一样的, k的约束已经没有作用了。所以dp数组可以去掉k这个维度.
• 因为冷冻期的存在, 第i天如果手上有股票而且选择了要买股票的时候应该是从第i-2天开始状态转移, 注意下方代码中的dp[i-2][0] - prices[i-1]

则dp状态转移方程得改改(忽略下方注释中的t), 如下:

# i天t次交易现在手上持有 = max(i-1天t次交易手上持有，i-2天t-1次交易手上不持有 - i天买入价格)
dp[i][1] = max(
    dp[i-1][1],
    # 为什么是`prices[i-2]`呢? 因为这里的i是第i天,
    # 根据我们的dp定义, 
    # 实际上第i=1天对应的是数组中的prices[0]的价格
    # 我们dp对交易的定义是买入就算, 这里买入第i天的一张股票, 得减去`prices[i-1]`
    # 所以我们这里才`t-1`, 好理解一些
    dp[i-2][0] - prices[i-1]
)
# i天t次交易现在手上不持有 = max(i-1天t次交易手上不持有，i-1天t次交易手上持有 + i天卖出价格prices)
dp[i][0] = max(
    dp[i-1][0],
    dp[i-1][1] + prices[i-1]
)

stock6

lc714
你可以无限次地完成交易，但是你每笔交易都需要付手续费。

题目特点:

• 可无限次交易, 则k还是无穷大, 那么就可以认为 k 和 k - 1 是一样的, k的约束已经没有作用了。所以dp数组可以去掉k这个维度.
• 手续费的存在, 根据我们dp的定义, 我们定义购买即为一次交易, 那我们就在每次购买的时候加上这个手续费, 则第i天如果手上有股票而且选择了要买股票的时候应该加上手续费, 注意下方代码中的dp[i-1][0] - prices[i-1] - fee

则dp状态转移方程得改改(忽略下方注释中的t), 如下:

# i天t次交易现在手上持有 = max(i-1天t次交易手上持有，i-1天t-1次交易手上不持有 - i天买入价格)
dp[i][1] = max(
    dp[i-1][1],
    # 为什么是`prices[i-1]`呢? 因为这里的i是第i天,
    # 根据我们的dp定义, 
    # 实际上第i=1天对应的是数组中的prices[0]的价格
    # 我们dp对交易的定义是买入就算, 这里买入一张股票, 得减去`prices[i-1]`
    # 所以我们这里才`t-1`, 好理解一些
    dp[i-1][0] - prices[i-1] - fee
)
# i天t次交易现在手上不持有 = max(i-1天t次交易手上不持有，i-1天t次交易手上持有 + i天卖出价格prices)
dp[i][0] = max(
    dp[i-1][0],
    dp[i-1][1] + prices[i-1]
)

打家劫舍系列

rob1

leetcode198题
你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

示例 1：
输入：[1,2,3,1]
输出：4
解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：
输入：[2,7,9,3,1]
输出：12
解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。

参考
题目很容易理解，而且动态规划的特征很明显。我们前文 动态规划详解 做过总结，解决动态规划问题就是找「状态」和「选择」，仅此而已。
假想你就是这个专业强盗，从左到右走过这一排房子，在每间房子前都有两种选择：抢或者不抢。

• 如果你抢了这间房子，那么你肯定不能抢相邻的下一间房子了，只能从下下间房子开始做选择。
• 如果你不抢这间房子，那么你可以走到下一间房子前，继续做选择。

当你走过了最后一间房子后，你就没得抢了，能抢到的钱显然是 0（base case）。
以上的逻辑很简单吧，其实已经明确了「状态」和「选择」：你面前房子的索引就是状态，抢和不抢就是选择。
在两个选项中选择偷窃总金额较大的选项，该选项对应的偷窃总金额即为从index开始偷到最后的房子能偷到的最高总金额.
用 dp[i] 表示从index开始偷到最后的房子能偷到的最高总金额，那么就有如下的状态转移方程：
dp[i] = max( dp[i+2] + nums[i], dp[i+1] )
边界条件为：

• dp[n-1] = nums[n-1] , 最后一间房屋，则偷窃该房屋
• dp[n-2] = max( nums[n-1], nums[n-2] ) , 最后两间房屋，选择其中金额较高的房屋进行偷窃

最终的答案即为 dp[n−1]，其中 n 是数组的长度
递归memo写法:

def rob1_dp_memo(self, nums_arr):
    return self._do_rob1_dp_memo(nums_arr, 0)

def _do_rob1_dp_memo(self, nums_arr, index):
    # 我们定义此函数为从index开始偷到最后的房子能偷到的最高总金额
    if index >= len(nums_arr):
        return 0
    if index in self._memo:
        return self._memo[index]
    res = max(
        nums_arr[index] + self._do_rob1_dp_memo(nums_arr, index+2),
        self._do_rob1_dp_memo(nums_arr, index+1),
    )
    self._memo[index] = res
    return res

迭代写法:

def rob1_dp(self, nums_arr):
    if not nums_arr:
        return 0
    n = len(nums_arr)
    dp = [0] * n
    dp[n-1] = nums_arr[n-1]
    dp[n-2] = max(nums_arr[n-1], nums_arr[n-2])
    for i in range(n-3, -1, -1):
        dp[i] = max(dp[i+1], nums_arr[i]+dp[i+2])
    return dp[0]

rob1进阶-求出具体偷哪些房子的子序列

还是用动规思路

def house_rob_detail_seq(self, nums_arr):
    if not nums_arr:
        return 0
    n = len(nums_arr)
    # 根据上述思路, 我们用 dp[i] 表示从第 i 间房屋偷到最后一间能偷窃到的最
    # 高总金额的房子数组子序列
    dp = [ [] for _ in xrange(n) ]
    dp[n-1] = [nums_arr[n-1]]
    dp[n-2] = [max(nums_arr[n-1], nums_arr[n-2])]
    for i in range(n-3, -1, -1):
        if (nums_arr[i] + sum(dp[i+2])) > sum(dp[i+1]):
            dp[i] = [nums_arr[i]] + dp[i+2]
        else:
            dp[i] = dp[i+1]
    return dp[0]

rob2

lc213
这道题目和第一道描述基本一样，强盗依然不能抢劫相邻的房子，输入依然是一个数组，但是告诉你这些房子不是一排，而是围成了一个圈。

也就是说，现在第一间房子和最后一间房子也相当于是相邻的，不能同时抢。比如说输入数组nums=[2,3,2]，算法返回的结果应该是 3 而不是 4，因为开头和结尾不能同时被抢。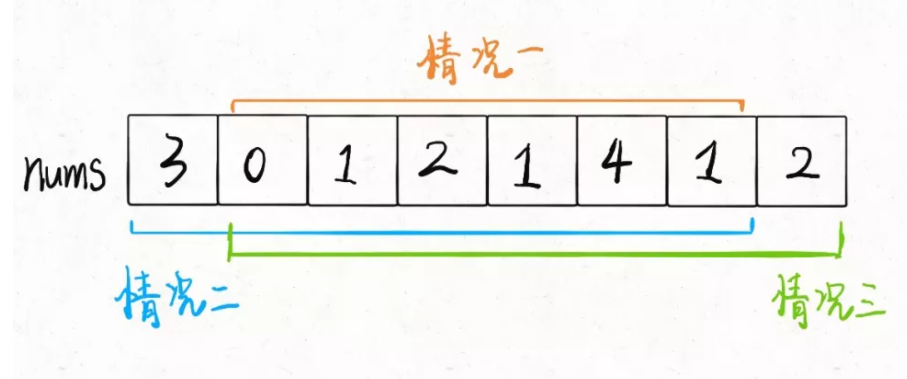

那就简单了啊，这三种情况，哪种的结果最大，就是最终答案呗！不过，其实我们不需要比较三种情况，只要比较情况二和情况三就行了，因为这两种情况对于房子的选择余地比情况一大呀，房子里的钱数都是非负数，所以选择余地大，最优决策结果肯定不会小。
所以只需对之前的解法调用一下求个max值即可：

def rob2_dp(nums_arr):
    n = len(nums_arr)
    max(rob1_dp(nums_arr[0:n-1]), rob1_dp(nums_arr[1:n])

rob3

lc337
第三题的房子在二叉树的节点上，相连的两个房子不能同时被抢劫：
示例 1:
输入: [3,2,3,null,3,null,1]

  3
 / \
2   3
 \   \ 
  3   1

输出: 7
解释: 小偷一晚能够盗取的最高金额 = 3 + 3 + 1 = 7.
示例 2:
输入: [3,4,5,1,3,null,1]

     3
   / \
  4   5
 / \   \ 
1   3   1

输出: 9
解释: 小偷一晚能够盗取的最高金额 = 4 + 5 = 9.

整体的思路完全没变，还是做抢或者不抢的选择，取收益较大的选择。甚至我们可以直接按这个套路写出递归式的dp代码：

def rob3_dp(self, bt):
    # 此函数求出bt为根节点的最大价值
    if not bt:
        return 0
    if bt in memo:
        return memo[bt]
    # 抢, 然后去下下家
    do_it = bt.val + \
        (rob3_dp(bt.left.left) + rob3_dp(bt.left.right) if bt.left else 0) + \
        (rob3_dp(bt.right.left) + rob3_dp(bt.right.left) if bt.right else 0)
    # 不抢, 然后去下家
    not_do_it = rob3_dp(bt.left) + rob3_dp(bt.right)
    res = max(do_it, not_do_it)
    memo[bt] = res
    return res

LIS问题-最长上升子序列

leetcode300题
LIS即longest-increasing-subsequence
给定一个无序的整数数组，找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。
说明:
可能会有多种最长上升子序列的组合，你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?

参考
我们定义 dp[i] 为选取到第i个数字的时候的最长上升子序列的长度, 注意这里的定义, 第i个数字是一定要选取的
则我们的状态转移方程为: dp[i] = max(dp[j]) + 1 , 其中 0 <= j < i 且 nums[j] < nums[i]

即考虑往 dp[0…i−1] 中最长的上升子序列后面再加一个 nums[i]。由于 dp[j]dp[j] 代表 nums[0…j] 中以 nums[j] 结尾的最长上升子序列，所以如果能从 dp[j]dp[j] 这个状态转移过来，那么 nums[i] 必然要大于 nums[j]，才能将 nums[i] 放在 nums[j] 后面以形成更长的上升子序列。
最后，整个数组的最长上升子序列即所有 dp[i]dp[i] 中的最大值。
LIS =max(dp[i]), 其中 0 ≤ i < n
下图显示了该方法：

翻译成代码就是:

class Solution_LIS(object):
    def lengthOfLIS(self, nums):
        """
        :type nums: List[int]
        :rtype: int
        """
        if not nums:
            return 0
        n = len(nums)
        # 我们定义 `dp[i]` 为选取到第i个数字的时候的最长上升子序列的长度,
        # 注意这里的定义, 第i个数字是一定要选取的.
        dp = [1] * n  # 因为自己本身就是一个长度为1的上升子序列
        dp[0] = 1
        for i in xrange(1, n):
            for j in xrange(0, i):
                # 则我们的状态转移方程为: 
                # `dp[i] = max(dp[j]) + 1 , 其中 0 <= j < i 且 nums[j] < nums[i]`
                if nums[j] < nums[i]:
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)

LIP问题-字跳一面-真正理解递推

lc329, hard
给定一个整数矩阵，找出最长递增路径的长度。对于每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外（即不允许环绕）。
示例 1:
输入:

nums = 
[
  [9,9,4],
  [6,6,8],
  [2,1,1]
]

输出: 4
解释: 最长递增路径为 [1, 2, 6, 9]。
示例 2:
输入:

nums = 
[
  [3,4,5],
  [3,2,6],
  [2,2,1]
]

输出: 4
解释: 最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

由lc300-lis问题-最长上升子序列, 我们很容易得出

• 状态定义dp[i][j] 为选中 matrix[i][j] 的最长递增路径的长度, 注意这里的 matrix[i][j]是一定要选中的
• dp[i][j] = 1, 都初始化为1, 因为根据状态定义, 即使相邻结点都小于自己, 那也至少为1
• 根据当前的元素和相邻上下左右的元素比较, 选出最大值再加1, 则为当前的dp, 故状态转移方程为:

  dp[i][j] = 1 + max(
      dp[i-1][j] if i-1 >= 0 and matrix[i-1][j] < matrix[i][j] else 0,  # 上
      dp[i][j-1] if j-1 >= 0 and matrix[i][j-1] < matrix[i][j] else 0,  # 左
      dp[i+1][j] if i+1 <= m-1 and matrix[i+1][j] < matrix[i][j] else 0,  # 下
      dp[i][j+1] if j+1 <= n-1 and matrix[i][j+1] < matrix[i][j] else 0  # 右
  )

这个题目如果没有真正理解递推, 很容易写错: 以为直接拿着matrix就两重for循环遍历就完了.
这样写是不对的, 因为要求的是递增路径, 所以我们得先根据matrix中每个元素值的大小按照从小到大排序,
然后从最小值的元素开始遍历一步步由小到大递推到最大一个点,
这样才算是考虑完全了, 这样才是从最小信息量的状态一点一点转移递推到大的状态的动态规划的过程.

代码如下:

def longestIncreasingPath(self, matrix):
    """
    :type matrix: List[List[int]]
    :rtype: int
    """
    if not matrix:
        return 0
    m = len(matrix)
    n = len(matrix[0])
    # * 状态定义`dp[i][j]` 为选中 `matrix[i][j]` 的最长递增路径的长度, 注意这里的 `matrix[i][j]`是一定要选中的
    # * `dp[i][j] = 1`, 都初始化为1, 因为根据状态定义, 即使相邻结点都小于自己, 那也至少为1
    dp = [ [ 1 for _ in range(n) ] for _ in range(m) ]
    points_list = []
    for i in range(m):
        for j in range(n):
            points_list.append([ matrix[i][j], i, j ])
    # 这个题目**如果没有真正理解递推, 很容易写错: 以为直接拿着matrix就两重for循环遍历就完了.**  
    # **这样写是不对的, 因为要求的是递增路径, 所以我们得先根据matrix中每个元素值的大小按照从小到大排序**,   
    # 然后从最小值的元素开始遍历一步步由小到大递推到最大一个点,  
    # 这样才算是考虑完全了, 这样才是从最小信息量的状态一点一点转移递推到大的状态的动态规划的过程.
    sorted_points_list = sorted(points_list, key=lambda x: x[0])
    for val, i, j in sorted_points_list:
        dp[i][j] = 1 + max(
            dp[i-1][j] if i-1 >= 0 and matrix[i-1][j] < matrix[i][j] else 0,  # 上
            dp[i][j-1] if j-1 >= 0 and matrix[i][j-1] < matrix[i][j] else 0,  # 左
            dp[i+1][j] if i+1 <= m-1 and matrix[i+1][j] < matrix[i][j] else 0,  # 下
            dp[i][j+1] if j+1 <= n-1 and matrix[i][j+1] < matrix[i][j] else 0  # 右
        )
    max_path_len = 0
    for i in range(m):
        for j in range(n):
            if dp[i][j] > max_path_len:
                max_path_len = dp[i][j]
    return max_path_len

LCS问题-最长公共子序列问题

lc1143
LCS即Longest-Common-Sequence
给出两个字符串S1和S2, 求这两个字符串最长公共子序列的长度.
比如:

• S1 = ABCD
• S2 = AEBD

则最长公共子序列为ABD, 其长度为3, 给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列，则返回 0。


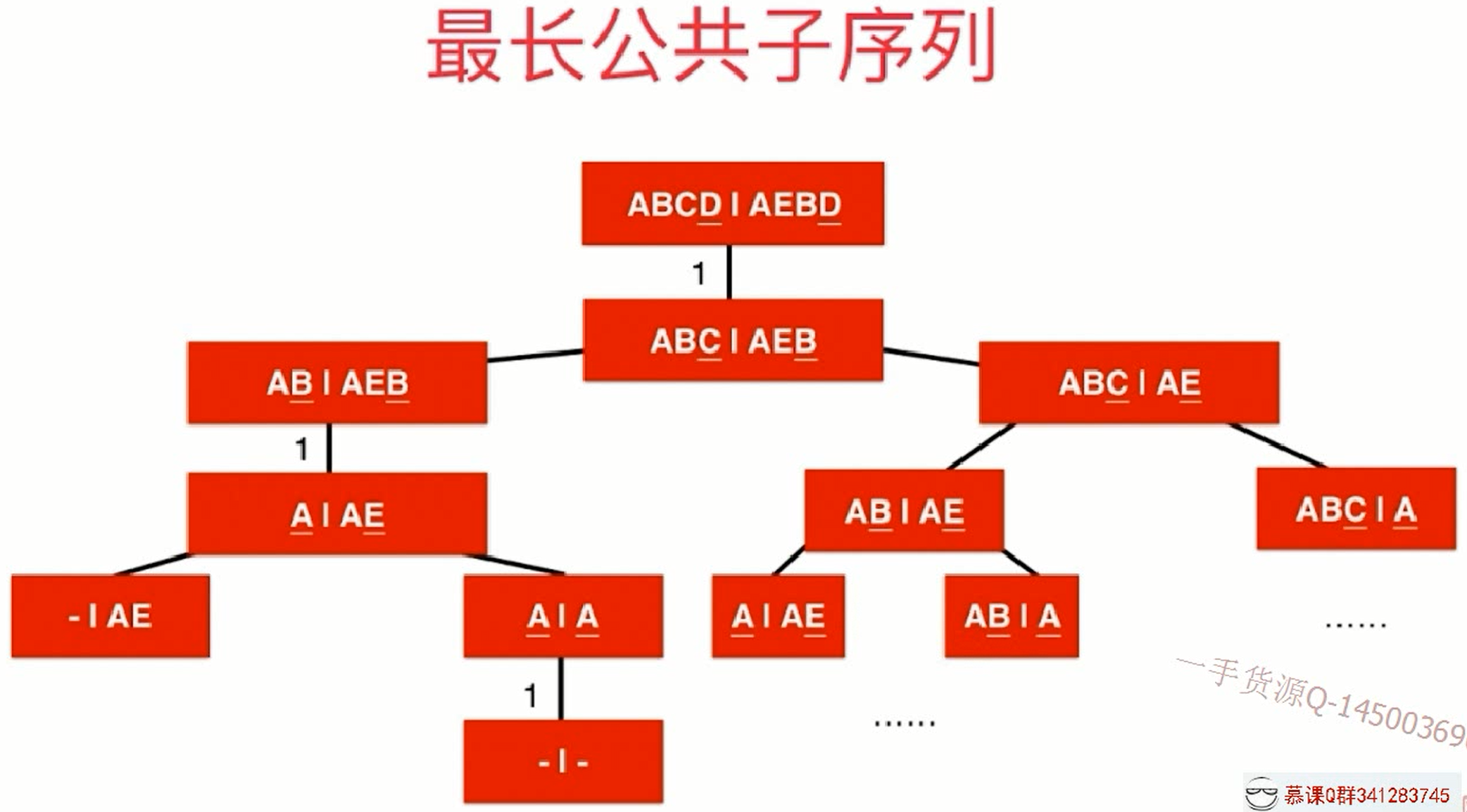
则代码如下:

class Solution_LCS(object):
    def lengthOfLCS(self, str_arr):
        if not str_arr:
            return 0
        assert len(str_arr) == 2
        str_a = str_arr[0]
        str_b = str_arr[1]
        m = len(str_a)
        n = len(str_b)
        if m < 1 or n < 1:
            return 0
        # 我们定义dp[i][j] 为 str_a[0...i] 和str_b[0...j]的最长子序列的长度
        dp = [ [ 0 for _ in xrange(n) ] for _ in xrange(m) ]
        # 初始化最底层的基础数据
        for k in xrange(n):
            dp[0][k] = 1 if str_a[0] == str_b[k] else 0
        for h in xrange(m):
            dp[h][0] = 1 if str_a[h] == str_b[0] else 0

        for i in xrange(1, m):
            for j in xrange(n):
                # 根据图中的状态转移方程得出, 有两种情况, 所以if一下
                if str_a[i] == str_b[j]:
                    dp[i][j] = dp[i-1][j-1] + 1
                else:
                    dp[i][j] = max(dp[i-1][j], dp[i][j-1] if j-1 >= 0 else 0)
        return dp[m-1][n-1]

求LCS具体的是哪个子序列

• 思路1: 还是用动规来解

  def get_lcs_detail_seq_1(self, str_arr):
      if not str_arr:
          return ""
      assert len(str_arr) == 2
      str_a = str_arr[0]
      str_b = str_arr[1]
      m = len(str_a)
      n = len(str_b)
      if m < 1 or n < 1:
          return ""
      # 我们定义dp[i][j] 为 str_a[0...i] 和str_b[0...j]的最长子序列
      dp = [ [ "" for _ in xrange(n) ] for _ in xrange(m) ]
      # 初始化最底层的基础数据
      for k in xrange(n):
          if str_a[0] == str_b[k]:
              for h in xrange(k, n):  # k后面的也都要设置
                  dp[0][h] = str_a[0]
      for k in xrange(m):
          if str_a[k] == str_b[0]:
              for h in xrange(k, m):  # k后面的也都要设置
                  dp[h][0] = str_b[0]
  
      for i in xrange(1, m):
          for j in xrange(1, n):
              # 根据图中的状态转移方程得出, 有两种情况, 所以if一下
              if str_a[i] == str_b[j]:
                  dp[i][j] = dp[i-1][j-1] + str_a[i]
              else:
                  dp[i][j] = dp[i-1][j] if len(dp[i-1][j]) > len(dp[i][j-1]) else dp[i][j-1]
      return dp[m-1][n-1]

• 思路2, 仅用来加深理解:
  不管是LCS/LIS/0-1背包问题如果要求最优解的具体情况是哪种, 我们的思路就是要用dp解法求出整个dp数组之后, 然后根据dp的状态定义, 以及dp数组里具体存储了的信息反推回去.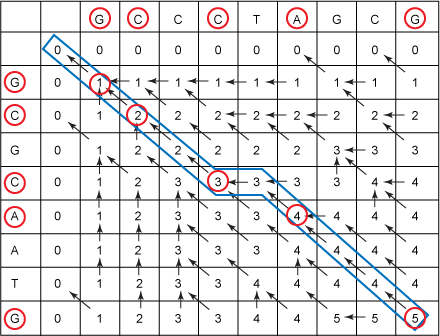

  
  从之前求lcs的代码以及上图中都可以看出, 从dp数组的末尾后面反推回去, 上一个公共字符所在的横纵index肯定在当前横纵index的左上.
  那则对于LCS的具体解, 思路2的代码如下:

  def get_lcs_detail_seq_2(self, str_arr):
      if not str_arr:
          return ""
      assert len(str_arr) == 2
      str_a = str_arr[0]
      str_b = str_arr[1]
      m = len(str_a)
      n = len(str_b)
      if m < 1 or n < 1:
          return ""
      # 我们定义dp[i][j] 为 str_a[0...i] 和str_b[0...j]的最长子序列的长度
      dp = [ [ 0 for _ in xrange(n) ] for _ in xrange(m) ]
      # 初始化最底层的基础数据
      for k in xrange(n):
          if str_a[0] == str_b[k]:
              for h in xrange(k, n):  # k后面的也都要置为1
                  dp[0][h] = 1
      for k in xrange(m):
          if str_a[k] == str_b[0]:
              for h in xrange(k, m):  # k后面的也都要置为1
                  dp[h][0] = 1
  
      for i in xrange(1, m):
          for j in xrange(1, n):
              # 根据图中的状态转移方程得出, 有两种情况, 所以if一下
              if str_a[i] == str_b[j]:
                  dp[i][j] = dp[i-1][j-1] + 1
              else:
                  dp[i][j] = max(dp[i-1][j], dp[i][j-1])
      # 不管是LCS/LIS/0-1背包问题如果要求最优解的具体情况是哪种, 
      # 我们的思路就是要用dp解法求出整个dp数组之后,
      # 然后根据dp的状态定义, 以及dp数组里具体存储了的信息反推回去.  
      #
      # 从之前求lcs的代码以及上图中都可以看出,
      # 从dp数组的末尾后面反推回去,
      # 上一个公共字符所在的横纵index肯定在当前横纵index的左上.
      p = len(str_a) - 1;
      q = len(str_b) - 1;
      _lcs_detail_seq = "";
      while(p >= 0 and q >= 0):
          if( str_a[p] == str_b[q] ):
              _lcs_detail_seq = str_a[p] + _lcs_detail_seq;
              p -= 1;
              q -= 1;
          elif(p == 0):
              q -= 1;
          elif(q == 0):
              p -= 1;
          else:
              # 由dp数组图中可知, 
              # 上一个公共字符所在的横纵index肯定在当前横纵index的左上.
              if(dp[p-1][q] > dp[p][q-1]):
                  # dp[p-1][q] 大, 则往左移动, p减一
                  # 这样才能才能找到最大公共子串的上一个公共字符嘛
                  p -= 1;
              else:
                  # dp[p][q-1] 大, 则往上移动, q减一
                  # 这样才能才能找到最大公共子串的上一个公共字符嘛
                  q -= 1;
      return _lcs_detail_seq;

谷歌经典扔鸡蛋问题

lc887
题目是这样：你面前有一栋从 1 到N共N层的楼，然后给你K个鸡蛋（K至少为 1）。现在确定这栋楼存在楼层0 <= F <= N，在这层楼将鸡蛋扔下去，鸡蛋恰好没摔碎（高于F的楼层都会碎，低于F的楼层都不会碎）。现在问你，最坏情况下，你至少要扔几次鸡蛋，才能确定这个楼层F呢？

举个例子来说明题意, 比如10层楼, 2个鸡蛋A和B, 最优解是 4 次. 这个4次是怎么算出来的呢? 随意举几种情况:

• 从5楼扔A, A碎了就扔另一个蛋B到0-4层, A没碎就继续扔B到6-10层
  • 最好的情况是: A第一次扔没碎, 然后到第6层碎了, 只扔了2次
  • 最坏: A第一次扔没碎, 然后到第10层都没碎, 扔了6次
• 从2楼/4/6/8/10扔A, A碎了就扔另一个蛋B, 比如在4楼A碎了就到3楼扔B
  • 最好的情况是: A第一次扔就碎了, 然后B到1楼去扔, 只扔了2次
  • 最坏: A一直扔到10楼才碎, 然后B到第9层去试试, 扔了6次
• 统计出来, 实际上最优的扔法是: A从第4楼/7/9/10这样扔
  • 最好的情况是: A第一次扔就碎了, 然后B从1楼开始扔, 然后b在1楼就碎了, 只扔了2次
  • 最坏:
    • A一直扔到10楼才碎, 扔了4次
    • A第一次扔就碎了, 然后B从1楼开始扔, 然后b在3楼碎了, 扔了4次

如果题目没看懂, 建议看一下此视频的讲解.
参考
对动态规划问题，直接套我们以前多次强调的框架即可：这个问题有什么「状态」，有什么「选择」，然后穷举。

• 「状态」很明显，就是当前拥有的鸡蛋数K和需要测试的楼层数N。随着测试的进行，鸡蛋个数可能减少，楼层的搜索范围会减小，这就是状态的变化。
• 「选择」其实就是去选择哪层楼扔鸡蛋。回顾刚才的线性扫描和二分思路，二分查找每次选择到楼层区间的中间去扔鸡蛋，而线性扫描选择一层层向上测试。不同的选择会造成状态的转移。

现在明确了「状态」和「选择」，动态规划的基本思路就形成了：肯定是个二维的dp数组或者带有两个状态参数的dp函数来表示状态转移；外加一个 for 循环来遍历所有选择，择最优的选择更新结果 ：

# 当前状态为 (K 个鸡蛋，N 层楼)
# 返回这个状态下的最优结果
def dp(K, N):
    int res
    for 1 <= i <= N:
        res = min(res, 这次在第 i 层楼扔鸡蛋)
    return res

这段伪码还没有展示递归和状态转移，不过大致的算法框架已经完成了。
我们在第i层楼扔了鸡蛋之后，可能出现两种情况：鸡蛋碎了，鸡蛋没碎。注意，这时候状态转移就来了：

• 如果鸡蛋碎了，那么鸡蛋的个数K应该减一，搜索的楼层区间应该从[1..N]变为[1..i-1]共i-1层楼；
• 如果鸡蛋没碎，那么鸡蛋的个数K不变，搜索的楼层区间应该从 [1..N]变为[i+1..N]共N-i层楼。

因为我们要求的是最坏情况下扔鸡蛋的次数，所以取决于哪种情况的dp结果更大, 所以要max一下：

def dp(K, N):
    for 1 <= i <= N:
        # 最坏情况下的最少扔鸡蛋次数
        res = min(res, 
                  max( 
                        dp(K - 1, i - 1), # 碎
                        dp(K, N - i)      # 没碎
                     ) + 1 # 在第 i 楼扔了一次
                 )
    return res

递归的 base case 很容易理解：当楼层数N等于 0 时，显然不需要扔鸡蛋；当鸡蛋数K为 1 时，显然只能线性扫描所有楼层：

def dp(K, N):
    if K == 1: return N
    if N == 0: return 0
    ...

至此，其实这道题就解决了！只要添加一个备忘录消除重叠子问题即可：

def superEggDrop(self, K, N):
    memo = dict()
    def dp(K, N):
        # base case
        if K == 1: return N
        if N == 0: return 0
        # 避免重复计算
        if (K, N) in memo:
            return memo[(K, N)]

        res = float('INF')
        # 穷举所有可能的选择
        for i in range(1, N + 1):
            res = min(res, 
                        max(
                            dp(K, N - i), 
                            dp(K - 1, i - 1)
                            ) + 1
                    )
        # 记入备忘录
        memo[(K, N)] = res
        return res
    return dp(K, N)

def superEggDrop_dp(self, K, N):
    """
    :type K: int
    :type N: int
    :rtype: int
    """ 
    # dp[k][n]: 表示为当前状态为 k 个鸡蛋，面对 n 层楼的
    # 这个状态下最坏的情况的最少的扔鸡蛋的次数
    dp = [ [ p for p in range(N+1) ] for _ in range(K+1) ]
    for t in range(2, K+1):
        for q in range(1, N+1):
            for m in range(1, q):
                dp[t][q] = min(
                    dp[t][q],
                    max(
                        dp[t-1][m-1],  # 碎了
                        dp[t][q-m],  # 没碎
                    ) + 1
                )
    return dp[K][N]

这个算法的时间复杂度是多少呢？动态规划算法的时间复杂度就是子问题个数 × 函数本身的复杂度。
函数本身的复杂度就是忽略递归部分的复杂度，这里dp函数中有一个 for 循环，所以函数本身的复杂度是 O(N)。
子问题个数也就是不同状态组合的总数，显然是两个状态的乘积，也就是 O(KN)。
所以算法的总时间复杂度是 O(K*N^2), 空间复杂度为子问题个数，即 O(KN)。

扔鸡蛋逆向思路2-推荐

参考
dp[2][3]表示：

注意查看下方代码中的注释:

def superEggDrop2(self, K, N):
    """
    :type K: int
    :type N: int
    :rtype: int
    * 鸡蛋掉落，鹰蛋（Leetcode 887）：（经典dp）
    * 有 K 个鸡蛋，有 N 层楼，用最少的操作次数 Q 检查出鸡蛋的质量。
    *
    * 思路：
    * 本题应该逆向思维，若你有 K 个鸡蛋，你最多操作 Q 次，求 N 最大值。
    *
    * dp[i][j] = dp[i][j-1] + dp[i-1][j-1] + 1;
    * 解释：
    * 0.dp[i][j]：如果你还剩 i 个蛋，且最多只能操作 j 次了，所能确定的最高楼层。
    * 1.dp[i][j-1]：蛋没碎，因此该部分决定了所操作楼层的上面所能容纳的楼层最大值
    * 2.dp[i-1][j-1]：蛋碎了，因此该部分决定了所操作楼层的下面所能容纳的楼层最大值
    * 又因为第 j 次操作结果只和第 j-1 次操作结果相关，因此可以只用一维数组。此处略.
    *
    * 时复：O(K*根号(N))
    """ 

    # j 最多不会超过 N 次（线性扫描）
    # base case:
    # dp[0][..] = 0
    # dp[..][0] = 0
    dp = [ [ 0 for _ in range(N+1) ] for _ in range(K+1) ]
    j = 0
    while dp[K][j] < N:  # 也就是给你K个鸡蛋，允许测试j次，最坏情况下最多能测试N层楼
        j += 1  # 这个j为什么要减一而不是加一？之前定义得很清楚，这个j是一个允许的次数上界，而不是扔了几次。
        for i in range(1, K+1):
            dp[i][j] = dp[i][j-1] + dp[i-1][j-1] + 1
    return j

整数拆分

这一小节, 我们开始讨论最优子结构: 通过求子问题的最优解, 可以获得原问题的最优解.

leetcode343题
给定一个正整数 n，将其拆分为至少两个正整数的和，并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
说明: 你可以假设 n 不小于 2 且不大于 58。

示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

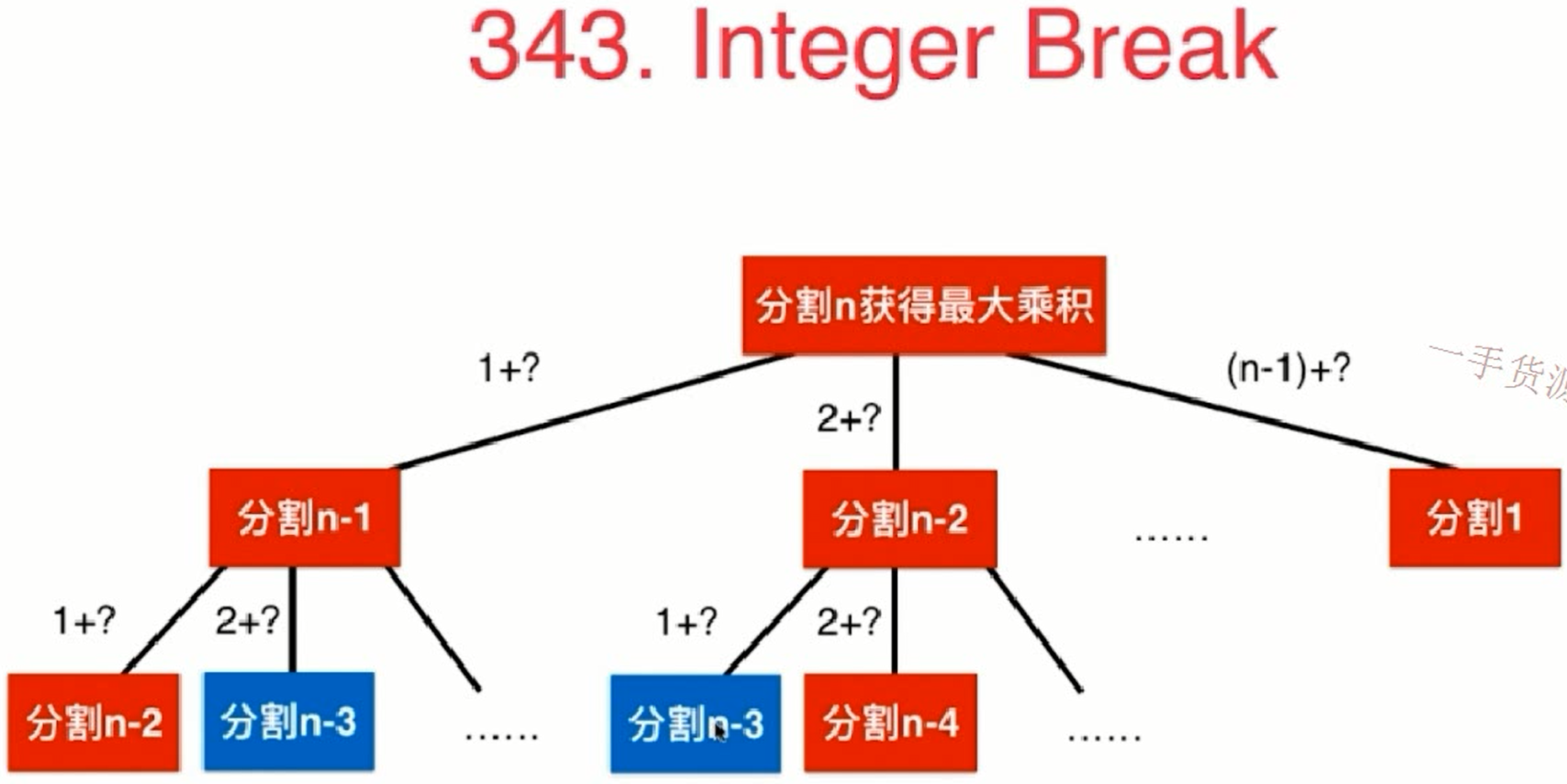
通过上图，我们很容易得到一个递归表达式：
F(n) = max {i * F(n - i)}，i = 1，2，... ，n - 1
上述表达式是表明n - i需要继续分解的情况，但如果i * (n - i)比F(n - i)要大，显然就不用再继续分解了。故我们还需要比较i * (n - i)与i * F(n - i)的大小关系。所以完整的表达式应该为：
F(n) = max { i * F(n - i), i * (n - i)} , i = 1, 2, ... , n - 1
基于此，就不难得到如下代码,
而通过以下代码中的 integer_break_dp 方法中的注释, 可以很清晰的看出怎么从普通递归一点一点演进到动态规划的思路的!
思路分析参考:

• https://leetcode-cn.com/problems/integer-break/solution/bao-li-sou-suo-ji-yi-hua-sou-suo-dong-tai-gui-hua-/
• https://leetcode-cn.com/problems/integer-break/solution/ba-yi-ba-zhe-chong-ti-de-wai-tao-343-zheng-shu-cha/

class Solution_integer_break(object):

    def __init__(self):
        self._memo = {}

    # 将n进行分割(至少分割两部分), 可以获得的最大乘积
    def integerBreak(self, n):
        """
        :type n: int
        :rtype: int
        """
        if n == 1:
            return 1
        _res = -1
        if n in self._memo:
            return self._memo[n]
        for i in xrange(1, n):
            # 计算`i + (n-i)`
            _res = max(
                _res,
                i * (n-i),  # 有可能自己本身`i*(n-i)`就是最大的
                i * self.integerBreak(n-i))
        self._memo[n] = _res
        return _res
        
    def integer_break_dp(self, n):
        # 下面这种A思路是不行的:
        # dp[i]等价于 f(i)，
        # 那么上面针对 f(i) 写的递归公式对 dp[i] 也是适用的，我们拿来试试。
        # 关键语句:
        #  `res = max(res, i * (n - i), max(i * self.integerBreak(n - i)))`
        # 翻译过来就是：`dp[i] = max(_res, i * (n-i), i * dp[n-i])`
        # 则不难得出以下代码, 但因为 dp[n-i] 当前没求出来, 子问题没求出来,
        # 所以原问题也就求不出来了, 所以下面这三行代码是不行的
        # _res = -1
        # for i in xrange(1, n):
            # dp[i] = max(_res, i * (n-i), i * dp[n-i])
        
        # 此时我们得下面这种B思路才行:
        # 我们用一层循环来生成上面这段A思路代码一系列的 n 值。
        # 接着我们还要生成上面A思路代码中一系列的 i 值，
        # 注意到 n - i 是要大于 0 的，
        # 因此 i 只需要循环到 n - 1 即可。
        # 由此不难翻译A思路得出以下代码(j代表n, k代表i):
        # dp[i] = max(dp[i], (i-j)*j, j* dp[i-j])  # j=1...i

        # dp[i] 表示将数字i分割(至少分割成两部分)后得到的最大乘积
        dp = [ float("-inf") for _ in range(n+1) ]
        dp[0] = float("-inf")
        dp[1] = float("-inf")
        dp[2] = 1
        for j in xrange(3, n+1):  # 循环到n
            for k in xrange(1, j):  # 循环到j-1即可
                dp[j] = max(dp[j], k*(j-k), k*dp[j-k])
        return dp[n]

双指针题型

两个无序数组的公共元素集合

思路: 两个集合求交集

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        unordered_set<int> set1, set2;
        for (auto& num : nums1) {
            set1.insert(num);
        }
        for (auto& num : nums2) {
            set2.insert(num);
        }
        return getIntersection(set1, set2);
    }

    vector<int> getIntersection(unordered_set<int>& set1, unordered_set<int>& set2) {
        if (set1.size() > set2.size()) {
            return getIntersection(set2, set1);
        }
        vector<int> intersection;
        for (auto& num : set1) {
            if (set2.count(num)) {
                intersection.push_back(num);
            }
        }
        return intersection;
    }
};

两个有序数组的公共元素集合

lc349, easy

关键是怎么用上有序这个定语

• 如果两个数组是有序的，则可以使用双指针的方法得到两个数组的交集。

• 首先对两个数组进行排序，然后使用两个指针遍历两个数组。可以预见的是加入答案的数组的元素一定是递增的，为了保证加入元素的唯一性，我们需要额外记录变量 pre 表示上一次加入答案数组的元素。初始时，两个指针分别指向两个数组的头部。每次比较两个指针指向的两个数组中的数字，如果两个数字不相等，则将指向较小数字的指针右移一位，如果两个数字相等，且该数字不等于 pre ，将该数字添加到答案并更新 pre 变量，同时将两个指针都右移一位。当至少有一个指针超出数组范围时，遍历结束

参考

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        sort(nums1.begin(), nums1.end());
        sort(nums2.begin(), nums2.end());
        int length1 = nums1.size(), length2 = nums2.size();
        int index1 = 0, index2 = 0;
        vector<int> intersection;
        while (index1 < length1 && index2 < length2) {
            int num1 = nums1[index1], num2 = nums2[index2];
            if (num1 == num2) {
                // 保证加入元素的唯一性
                if (!intersection.size() || num1 != intersection.back()) {
                    intersection.push_back(num1);
                }
                index1++;
                index2++;
            } else if (num1 < num2) {
                index1++;
            } else {
                index2++;
            }
        }
        return intersection;
    }
};

最小覆盖子串-滑动窗口典型题目

lc76, hard
参考
这里有一套滑动窗口算法的代码框架，我连在哪里做输出 debug 都给你写好了，以后遇到相关的问题，你就默写出来如下框架然后改三个地方就行，还不会出边界问题：

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0; 
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/

        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

其中两处…表示的更新窗口数据的地方，到时候你直接往里面填就行了。而且，这两个…处的操作分别是右移和左移窗口更新操作，等会你会发现它们操作是完全对称的。

我们继续就本题来谈滑动窗口算法的思路是这样：

1. 我们在字符串S中使用双指针中的左右指针技巧，初始化left = right = 0，把索引左闭右开区间[left, right)称为一个「窗口」。
2. 我们先不断地增加right指针扩大窗口[left, right)，直到窗口中的字符串符合要求（包含了T中的所有字符）。
3. 此时，我们停止增加right，转而不断增加left指针缩小窗口[left, right)，直到窗口中的字符串不再符合要求（不包含T中的所有字符了）。同时，每次增加left，我们都要更新一轮结果。
4. 重复第 2 和第 3 步，直到right到达字符串S的尽头。

这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解，也就是最短的覆盖子串。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动，这就是「滑动窗口」这个名字的来历。

下面画图理解一下，needs和window相当于计数器，分别记录T中字符出现次数和「窗口」中的相应字符的出现次数。
初始状态：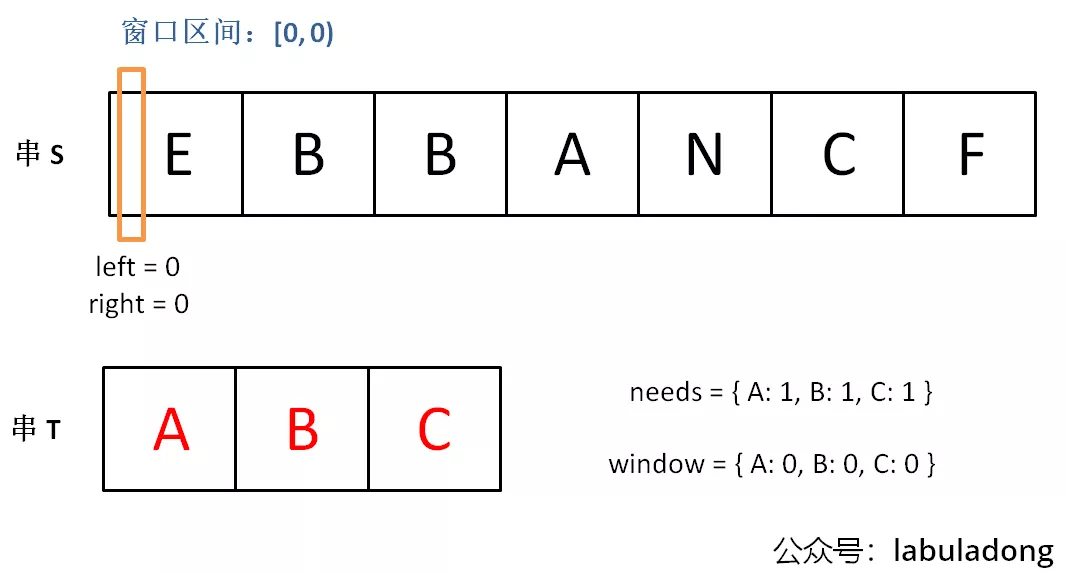

增加right，直到窗口[left, right)包含了T中所有字符：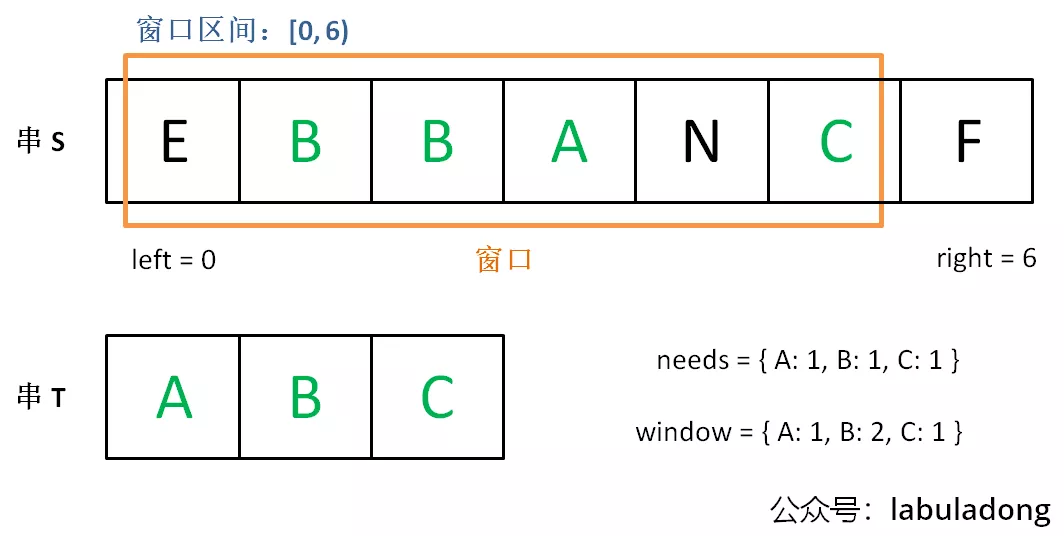

现在开始增加left，缩小窗口[left, right)。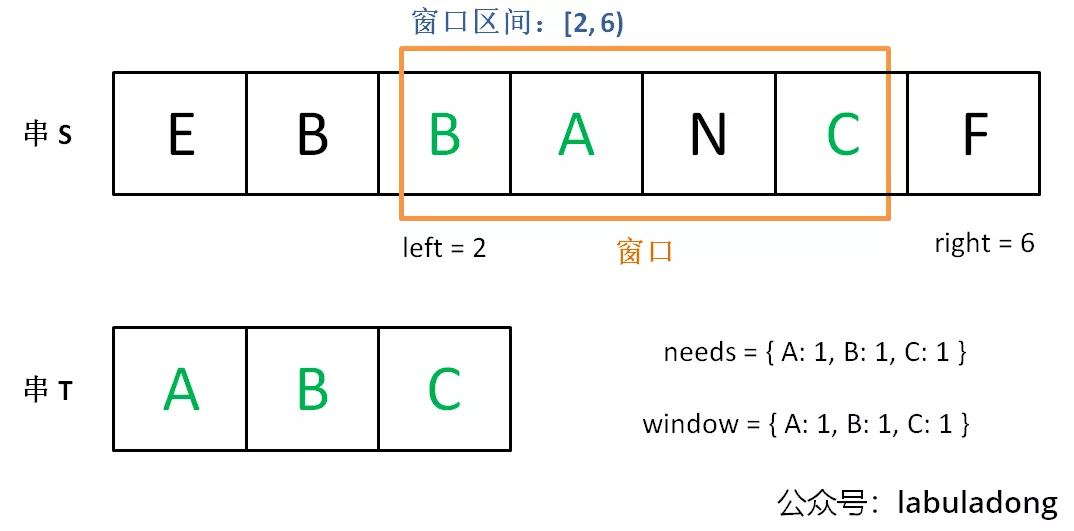

直到窗口中的字符串不再符合要求，left不再继续移动。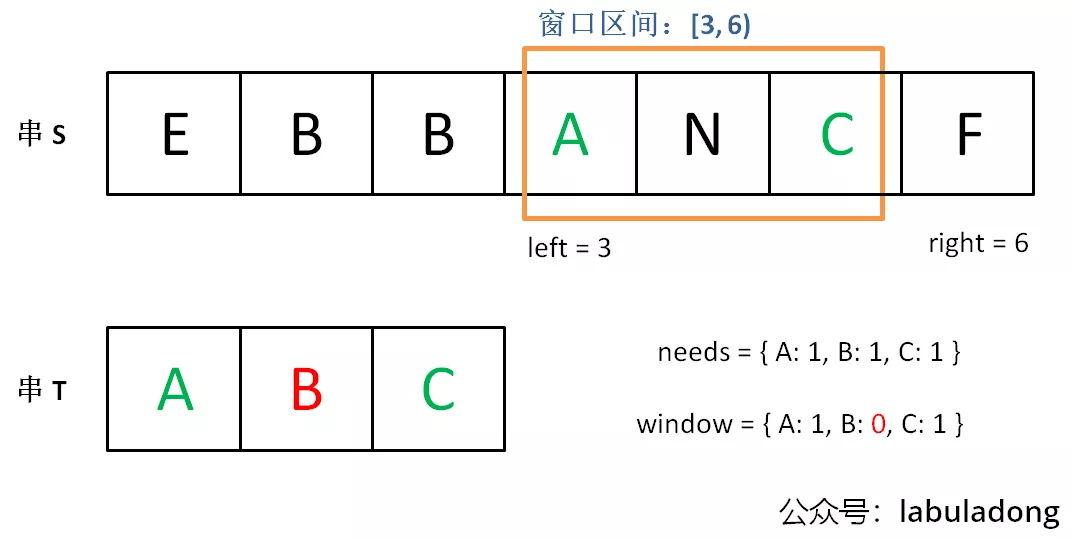

之后重复上述过程，先移动right，再移动left…… 直到right指针到达字符串S的末端，算法结束。
如果一个字符进入窗口，应该增加window计数器；如果一个字符将移出窗口的时候，应该减少window计数器；当valid满足need时应该收缩窗口；应该在收缩窗口的时候更新最终结果。
下面是完整代码：

string minWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    // 记录最小覆盖子串的起始索引及长度
    int start = 0, len = INT_MAX;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }
        // 判断左侧窗口是否要收缩
        while (valid == need.size()) {
            // 在这里更新最小覆盖子串
            if (right - left < len) {
                start = left;
                len = right - left;
            }
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }                    
        }
    }
    // 返回最小覆盖子串
    return len == INT_MAX ?
        "" : s.substr(start, len);
}

n数之和问题-双指针从两端逼近

参考

两数之和

先讨论两数之和, 解决思路就是先排序然后用两个指针从首尾两端逼近

为了防止结果重复, 指针应该向上图这样移动

vector<vector<int>> twoSum(vector<int>& nums, int target) {
    // nums 数组必须有序
    sort(nums.begin(), nums.end());
    int lo = 0, hi = nums.size() - 1;
    vector<vector<int>> res;
    while (lo < hi) {
        int sum = nums[lo] + nums[hi];
        int left = nums[lo], right = nums[hi];
        if (sum < target) {
            while (lo < hi && nums[lo] == left) lo++;
        } else if (sum > target) {
            while (lo < hi && nums[hi] == right) hi--;
        } else {
            res.push_back({left, right});
            // 跳过所有重复的元素
            while (lo < hi && nums[lo] == left) lo++;
            while (lo < hi && nums[hi] == right) hi--;
        }
    }
    return res;
}

三数之和

确定了第一个数字之后，剩下的两个数字可以是什么呢？其实就是和为 target - nums[i]的两个数字呗, 此时threeSum函数的实现思路就出来了:
先对数组排序, 然后遍历数组, 确定好第一个数字, 后面两个数字这两个数字用twoSum的双指针思路来求

四数之和

先对数组排序, 然后遍历数组, 确定好第一个数字, 后面三个数字这两个数字用threeSum函数来求

n数之和

以下代码看起来很长，实际上就是把之前的题目解法合并起来了，n == 2 时是 twoSum 的双指针解法，n > 2 时就是穷举第一个数字，然后递归调用计算 (n-1)Sum，组装答案。

需要注意的是，调用这个 nSum 函数之前一定要先给 nums 数组排序，因为 nSum 是一个递归函数，如果在 nSum 函数里调用排序函数，那么每次递归都会进行没有必要的排序，效率会非常低。

/* 注意：调用这个函数之前一定要先给 nums 排序 */
vector<vector<int>> nSumTarget(
    vector<int>& nums, int n, int start, int target) {

    int sz = nums.size();
    vector<vector<int>> res;
    // 至少是 2Sum，且数组大小不应该小于 n
    if (n < 2 || sz < n) return res;
    // 2Sum 是 base case
    if (n == 2) {
        // 双指针那一套操作
        int lo = start, hi = sz - 1;
        while (lo < hi) {
            int sum = nums[lo] + nums[hi];
            int left = nums[lo], right = nums[hi];
            if (sum < target) {
                while (lo < hi && nums[lo] == left) lo++;
            } else if (sum > target) {
                while (lo < hi && nums[hi] == right) hi--;
            } else {
                res.push_back({left, right});
                while (lo < hi && nums[lo] == left) lo++;
                while (lo < hi && nums[hi] == right) hi--;
            }
        }
    } else {
        // n > 2 时，递归计算 (n-1)Sum 的结果
        for (int i = start; i < sz; i++) {
            vector<vector<int>> 
                sub = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
            for (vector<int>& arr : sub) {
                // (n-1)Sum 加上 nums[i] 就是 nSum
                arr.push_back(nums[i]);
                res.push_back(arr);
            }
            while (i < sz - 1 && nums[i] == nums[i + 1]) i++;
        }
    }
    return res;
}

其他类型经典题

用Rand7实现Rand10

lc470, medium
已有方法 rand7 可生成 1 到 7 范围内的均匀随机整数，试写一个方法 rand10 生成 1 到 10 范围内的均匀随机整数。

• 参考
• 参考

为什么这道题不简单?

现在要从 rand7() 到 rand10()，也要求是等概率的，那只要我们把小的数映射到一个大的数就好办了，那首先想到的办法是乘个两倍试一试，每个 rand7() 它能生成数的范围是 1～7，rand 两次，那么数的范围就变为 2～14，哦，你可能发现没有 1 了，想要再减去个 1 来弥补，
rand(7)+rand(7)-1，其实这样是错误的做法，因为对于数字 5 这种，你有两种组合方式 (2+3 or 3+2)，而对于 14，你只有一种组合方式(7+7)，它并不是等概率的，那么简单的加减法不能使用，因为它会使得概率不一致，

下面我们系统的来分析:

Part1

假设已知rand2()可以均匀的生成 [1,2] 的随机数，现在想均匀的生成 [1,4] 的随机数，该如何考虑？

我想如果你也像我一样第一次接触这个问题，那么很可能会这么考虑——令两个rand2()相加，再做一些必要的边角处理。如下：

rand2() + rand2() = ? ==> [2,4]
   1    +   1     = 2
   1    +   2     = 3
   2    +   1     = 3
   2    +   2     = 4

// 为了把生成随机数的范围规约成[1,n]，于是在上一步的结果后减1
(rand2()-1) + rand2() = ? ==> [1,3]
   0       +   1     = 1
   0       +   2     = 2
   1       +   1     = 2
   1       +   2     = 3

可以看到，使用这种方法处理的结果，最致命的点在于——其生成的结果不是等概率的。在这个简单的例子中，产生 2 的概率是 50%，而产生 1 和 3 的概率则分别是 25%。原因当然也很好理解，由于某些值会有多种组合，因此仅靠简单的相加处理会导致结果不是等概率的。

因此，我们需要考虑其他的方法了。

仔细观察上面的例子，我们尝试对 (rand2()-1) 这部分乘以 2，改动后如下：

(rand2()-1) × 2 + rand2() = ? ==> [1,3]
   0            +   1     = 1
   0            +   2     = 2
   2            +   1     = 3
   2            +   2     = 4

神奇的事情发生了，奇怪的知识增加了。通过这样的处理，得到的结果恰是 [1,4] 的范围，并且每个数都是等概率取到的。因此，使用这种方法，可以通过rand2()实现rand4()。

也许这么处理只是我运气好，而不具有普适性？那就多来尝试几个例子。比如：

(rand9()-1) × 7 + rand7() = result
     a               b

为了表示方便，现将rand9()-1表示为 a，将rand7()表示为 b。计算过程表示成二维矩阵，如下：

可以看到，这个例子可以等概率的生成 [1,63] 范围的随机数。

规律

再提炼一下，可以得到这样一个规律：

已知 rand_N() 可以等概率的生成[1, N]范围的随机数
那么：
(rand_X() - 1) × Y + rand_Y() ==> 可以等概率的生成[1, X * Y]范围的随机数
即实现了 rand_XY()

Part2

那么想到通过rand4()来实现rand2()呢？这个就很简单了，已知rand4()会均匀产生 [1,4] 的随机数，通过取余，再加 1 就可以了。如下所示，结果也是等概率的。

rand4() % 2 + 1 = ?
   1 % 2    + 1 = 2
   2 % 2    + 1 = 1
   3 % 2    + 1 = 2
   4 % 2    + 1 = 1

事实上，只要rand_N()中 N 是 2 的倍数，就都可以用来实现rand2()，反之，若 N 不是 2 的倍数，则产生的结果不是等概率的。比如：

rand6() % 2 + 1 = ?
   1 % 2    + 1 = 2
   2 % 2    + 1 = 1
   3 % 2    + 1 = 2
   4 % 2    + 1 = 1
   5 % 2    + 1 = 2
   6 % 2    + 1 = 1

rand5() % 2 + 1 = ?
   1 % 2    + 1 = 2
   2 % 2    + 1 = 1
   3 % 2    + 1 = 2
   4 % 2    + 1 = 1
   5 % 2    + 1 = 2

Part3

ok，现在回到本题中。已知rand7()，要求通过rand7()来实现rand10()。

有了前面的分析，要实现rand10()，就需要先实现rand_N()，并且保证 N 大于 10 且是 10 的倍数。这样再通过rand_N() % 10 + 1 就可以得到 [1,10] 范围的随机数了。

而实现rand_N()，我们可以通过 part 1 中所讲的方法对rand7()进行改造，如下：

(rand7()-1) × 7 + rand7()  ==> rand49()

但是这样实现的 N 不是 10 的倍数啊！这该怎么处理？这里就涉及到了 “拒绝采样” 的知识了，也就是说，如果某个采样结果不在要求的范围内，则丢弃它。基于上面的这些分析，再回头看下面的代码，想必是不难理解了。

class Solution extends SolBase {
    public int rand10() {
        // 首先得到一个数
        int num = (rand7() - 1) * 7 + rand7();
        // 只要它还大于10，那就给我不断生成，因为我只要范围在1-10的，最后直接返回就可以了
        while (num > 10){
            num = (rand7() - 1) * 7 + rand7();
        }
        return num;
    }
}

这样的一个问题是，我们的函数会得到 1～49之间的数，而我们只想得到 1～10 之间的数，这一部分占的比例太少了，简而言之，这样效率太低，太慢，可能要 while 循环很多次，那么解决思路就是舍弃一部分数，舍弃 41～49，因为是独立事件，我们生成的 1～40 之间的数它是等概率的，我们最后完全可以利用 1～40 之间的数来得到 1～10 之间的数。所以，我们的代码可以改成下面这样

class Solution extends SolBase {
    public int rand10() {
        while(true) {
            int num = (rand7() - 1) * 7 + rand7(); // 等概率生成[1,49]范围的随机数
            if(num <= 40) return num % 10 + 1; // 拒绝采样，并返回[1,10]范围的随机数
        }
    }
}

Part4: 优化

更进一步，这时候我们舍弃了 9 个数，舍弃的还是有点多，效率还是不高，怎么提高效率呢？那就是舍弃的数最好再少一点！因为这样能让 while 循环少转几次，那么对于大于 40 的随机数，别舍弃呀，利用这 9 个数，再利用那个公式操作一下：

(大于40的随机数 - 40 - 1) * 7 + rand7()

这样我们可以得到 1−63 之间的随机数，只要舍弃 3 个即可，那对于这 3 个舍弃的，还可以再来一轮：

(大于60的随机数 - 60 - 1) * 7 + rand7()

这样我们可以得到 1−21 之间的随机数，只要舍弃 1 个即可。

/**
 * The rand7() API is already defined in the parent class SolBase.
 * public int rand7();
 * @return a random integer in the range 1 to 7
 */
class Solution extends SolBase {
    public int rand10() {
        while (true){
            int num = (rand7() - 1) * 7 + rand7();
            // 如果在40以内，那就直接返回
            if(num <= 40) return 1 + num % 10;
            // 说明刚才生成的在41-49之间，利用随机数再操作一遍
            num = (num - 40 - 1) * 7 + rand7();
            if(num <= 60) return 1 + num % 10;
            // 说明刚才生成的在61-63之间，利用随机数再操作一遍
            num = (num - 60 - 1) * 7 + rand7();
            if(num <= 20) return 1 + num % 10;

        }
    }
}

Algo noodle LeetCode

Cache和DB一致性

算法企业真题实战练习